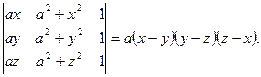Используя обратную матрицу, можно решить систему линейных уравнений, у которой число уравнений равно числу неизвестных, если det A ¹ 0.
Обозначим:
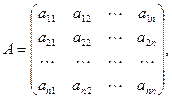  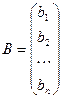 , ,
| (1.10.1) |
где X – матрица неизвестных, B – матрица свободных членов.
При таких обозначениях систему линейных уравнений
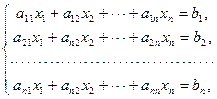
| (1.10.2) |
можно записать в матричной форме:
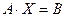
| (1.10.3) |
Умножим обе части полученного матричного уравнения слева на A–1: 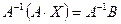 .
.
Далее, используя свойства произведения матриц, получим: (A -1∙ A)∙ X = A -1∙ B, E ∙ X = A -1∙ B,
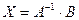
| (1.10.4) |
Итак, чтобы найти матрицу неизвестных, достаточно матрицу A–1, обратную матрице A, умножить на матрицу свободных членов.
Пример
Решить систему уравнений с помощью обратной матрицы:

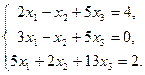
Решение
Обозначим:
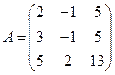 ,
, 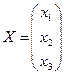 ,
, 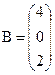 .
.
Вычислим определитель основной матрицы системы: det A =23≠0. Так как det A ¹0, систему можно решать матричным методом. Найдем матрицу A –1, обратную матрице A: 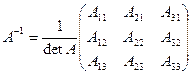 Вычислим алгебраические дополнения Aik (i, k = 1, 2, 3) к элементам aik матрицы A: A 11 = –23, A 12 = –14, A 13 = 11, A 21 = 23, A 22 = 1, A 23 = –9, A 31 = 0, A 32 = 5, A 33 = 1.
Вычислим алгебраические дополнения Aik (i, k = 1, 2, 3) к элементам aik матрицы A: A 11 = –23, A 12 = –14, A 13 = 11, A 21 = 23, A 22 = 1, A 23 = –9, A 31 = 0, A 32 = 5, A 33 = 1.
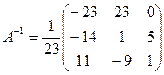
Проверим, верно ли найдена A –1:
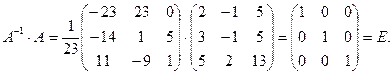
Матрица A –1 найдена верно. Находим матрицу неизвестных: 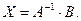
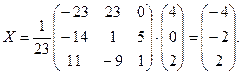
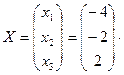 Итак, x 1 = –4, x 2 = –2, x 3 = 2. Проверим полученное решение: 2×(–4) – (–2) + 5×2 = –8 + 2 + 10 = 4, 3×(–4) – (–2) + 5×2 = –12 + 2 + 10 = 0, 5×(–4) + 2×(–2) + 13×2 = –20 – 4 + 26 = 2.
Итак, x 1 = –4, x 2 = –2, x 3 = 2. Проверим полученное решение: 2×(–4) – (–2) + 5×2 = –8 + 2 + 10 = 4, 3×(–4) – (–2) + 5×2 = –12 + 2 + 10 = 0, 5×(–4) + 2×(–2) + 13×2 = –20 – 4 + 26 = 2.
Метод Гаусса
Метод Гаусса (или метод последовательного исключения неизвестных) состоит в том, что посредством последовательного исключения неизвестных данная система
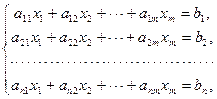
| (1.11.1) |
превращается в ступенчатую (в частности, треугольную) систему
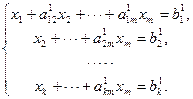
| (1.11.2) |
Последняя система равносильна данной, но решать ее намного проще. Переход системы (1.11.1) к равносильной ей системе (1.11.2) называется прямым ходом метода Гаусса, а нахождение переменных из системы (1.11.2) – обратным ходом.
Рассмотрим этот метод на конкретных примерах.
Пример
Решить систему методом Гаусса:
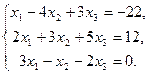
Решение
Исключим x1 из 2–го т 3–го уравнений. Для этого 1–е уравнение умножим на (–2) и прибавим его ко 2–му, а затем 1–е уравнение умножим на (–3) и прибавим его к 3–му уравнению:
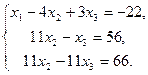
Новая система равносильна данной. Исключим из 3–го уравнения x2 для чего 2–е уравнение вычтем из 3–го:
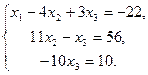
Из последней системы находим x3 = –1, x 2 = (56 + x 3)/11 = (56 – 1)/11 = 55/11 = 5, x 1 = –22 +4 x 2 – 3 x 3 = –22 + 4×5 – 3×(–1) = 1.
Пример
Решить систему методом Гаусса:
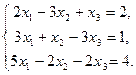
Решение
Умножим 2–е уравнение на (–2), а 1–е – на 3 и сложим, а затем 2–е уравнение умножим на (–5), а 3–е – на 3 и тоже сложим. Получим 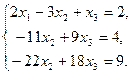 Исключим x2 из 3–го уравнения, умножив 2–е уравнение на (–2) и прибавив его к 3–му уравнению:
Исключим x2 из 3–го уравнения, умножив 2–е уравнение на (–2) и прибавив его к 3–му уравнению:
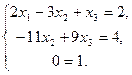
Последнее уравнение превратилось в неверное равенство. Это говорит о том, что система несовместна, т.е. решений не имеет.
Пример
Решить систему методом Гаусса:
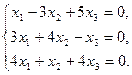
Решение
Исключим x1 из 2–го и 3–го уравнений. Для этого умножим 1–е уравнение на (–1) и прибавляем его ко 2–му, далее умножим 1–е же на (–4) и прибавляем к 3–му уравнению:

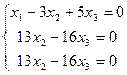
Так 2–е и 3–е уравнения одинаковы, одно из них отбрасываем:
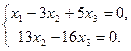
Число уравнений – два – меньше числа неизвестных – три. Такая система имеет бесчисленное множество решений. Пусть x 3 = 13 k, где k – произвольное число. Тогда x 2 = (16/13) x 3 = 16 k, x 1 = 3 x 2 – 5 x 3 = –17 k.
Преобразования Гаусса удобно проводить не с самой системой уравнений, а с матрицей ее коэффициентов. Введем матрицу
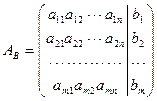
| (1.11.3) |
называемую расширенной матрицей системы (1.8.1) размера m ´(n +1), так как матрица А дополнена столбцом свободных членов.
Пример
Найти решение системы уравнений методом Гаусса.
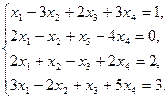
Решение
Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода Гаусса.
Шаг 1. Умножим первую строку матрицы AB на –2 и прибавим ее ко второй и третьей строке. Затем умножим первую строку матрицы AB на –3 и прибавим ее к четвертой строке. Получим
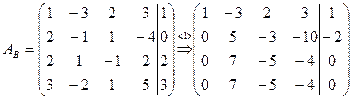 .
.
Поскольку две последние строки являются линейно зависимыми, то одну из них можно отбросить.
Шаг 2. Умножим вторую строку полученной матрицы на –7/5 и прибавим ее к третьей строке. Получим
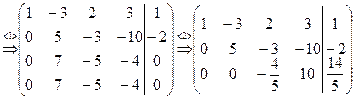 .
.
Заключительный вид расширенной матрицы соответствует совместной системе трех уравнений с четырьмя неизвестными, ранг которой меньше числа неизвестных. Полагая x 4 свободной переменной, получаем
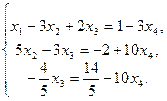
Из этой системы получаем обратным ходом метода Гаусса
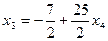 ,
, 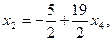
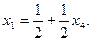
Данная система уравнений имеет бесчисленное множество решений, так как x 4 может принимать любые значения.
Отметим достоинства метода Гаусса по сравнению с методом обратной матрицы и методом Крамера:
- метод является значительно менее трудоемким;
- метод дает возможность однозначно установить, совместна система или нет, а в случае
совместности, найти ее решения;
- метод дает возможность найти максимальное число линейно независимых уравнений, т.е. определить ранг матрицы системы.
1.12. Системы m линейных уравнений с n неизвестными. Теорема Кронекера–Капелли
Пусть задана система линейных уравнений общего вида (1.8.1), где m £ n, т.е. число неизвестных не меньше числа уравнений. Вопрос о разрешимости системы (1.8.1) рассматривается в следующей теореме.
Теорема Кронекера–Капелли (критерий совместности системы).
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Не проводя строго доказательства теоремы, поясним его. В процессе преобразования системы уравнений (1.8.1) к виду (1.11.2), т.е элементарных преобразований матрицы системы  и расширенной матрицы
и расширенной матрицы 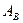 , ранги этих матриц не изменяются. Выше (п. 1.11) было установлено, что система (1.11.2) совместна тогда и только тогда, когда все свободные члены
, ранги этих матриц не изменяются. Выше (п. 1.11) было установлено, что система (1.11.2) совместна тогда и только тогда, когда все свободные члены 
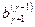 , …,
, …, 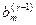 равны нулю. В этом случае, как нетрудно проверить, ранг матрицы и ранг расширенной матрицы системы (1.11.2), так же как и исходной системы (1.8.1) совпадают (оба равны r).
равны нулю. В этом случае, как нетрудно проверить, ранг матрицы и ранг расширенной матрицы системы (1.11.2), так же как и исходной системы (1.8.1) совпадают (оба равны r).
Представим общий порядок решения системы общего вида.
Необходимо определить совместность системы, т.е. определить ранги матрицы системы  и расширенной матрицы
и расширенной матрицы 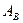 . Из теоремы Кронекера–Капелли следует, что если ранги этих матриц не совпадают, то система не совместна и нет смысла ее решать. Если же ранги матриц
. Из теоремы Кронекера–Капелли следует, что если ранги этих матриц не совпадают, то система не совместна и нет смысла ее решать. Если же ранги матриц  и
и 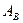 равны, то система совместна.
равны, то система совместна.
Для совместных систем линейных уравнений справедливы следующие теоремы:
– если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.
– если ранг матрицы совместной системы меньше числа переменных, т.е. r<n, то система (1.8.1) неопределенная и имеет бесконечное множество решений.
Результаты исследования системы (1.8.1) приведены в виде схемы на рис. 1.1.
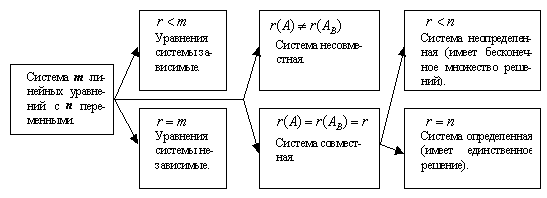
Рис. 1.1. Исследование системы линейных уравнений
1.13. n–мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, в которых определены операции сложения и умножения на число, являются простейшими примерами векторных пространств. Здесь мы приведем обобщение этих понятий на n –мерный случай.
Определение
Любой упорядоченный набор из n действительных чисел 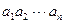 называется n–мерным вектором
называется n–мерным вектором  ; при этом числа, составляющие упомянутый набор, называются координатами вектора
; при этом числа, составляющие упомянутый набор, называются координатами вектора  .
.
Координаты n –мерного вектора  можно расположить либо в строку
можно расположить либо в строку 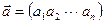 (вектор–строка), либо в столбец (вектор–столбец)
(вектор–строка), либо в столбец (вектор–столбец) 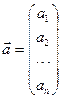 .
.
Определение
Два n –мерных вектора равны тогда и только тогда, когда равны их соответствующие координаты, т.е. 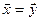 , если
, если 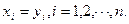
Определение
Суммой двух n –мерных векторов называется вектор 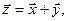 , компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.,
, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е., 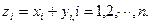
Определение
Произведением n –мерного вектора 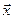 на действительное число l называется вектор
на действительное число l называется вектор 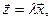 , компоненты которого равны произведению l на соответствующие компоненты вектора
, компоненты которого равны произведению l на соответствующие компоненты вектора 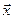 , т.е.,
, т.е., 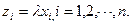 ,.
,.
Линейные операции над n –мерными векторами удовлетворяют следующим свойствам:
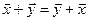 – перемести тельное свойство;
– перемести тельное свойство;
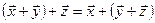 – сочетательное свойство;
– сочетательное свойство;

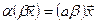 – сочетательное относительно числового множителя свойство;
– сочетательное относительно числового множителя свойство;
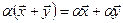 – распределительное относительно суммы векторов свойство;
– распределительное относительно суммы векторов свойство;
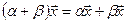 – распределительное относительно суммы числовых множителей свойство;
– распределительное относительно суммы числовых множителей свойство;
Существует нулевой вектор 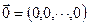 такой, что
такой, что 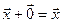 для любого вектора
для любого вектора 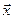 .
.
Для любого вектора 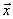 существует противоположный вектор
существует противоположный вектор 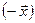 такой, что
такой, что 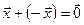 ;
;
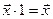 для любого вектора
для любого вектора 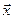 .
.
Определение
Совокупность 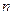 –мерных векторов, для которых определены операции сложения векторов и умножения вектора на число, и удовлетворяющих приведенным выше свойствам, называется линейным векторным пространством
–мерных векторов, для которых определены операции сложения векторов и умножения вектора на число, и удовлетворяющих приведенным выше свойствам, называется линейным векторным пространством 
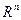 .
.
Евклидово пространство
Выше мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.
Определение
Скалярным произведением двух векторов x = 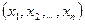 и y =
и y = 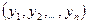 называется число
называется число
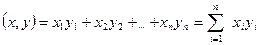
| (1.16.1) |
Скалярное произведение имеет следующие свойства:
1. 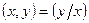 – коммутативное свойство.
– коммутативное свойство.
2. 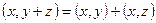 – дистрибутивное свойство.
– дистрибутивное свойство.
3. 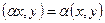 –для любого действительного числа α.
–для любого действительного числа α.
4. 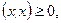 , если x ненулевой вектор,
, если x ненулевой вектор, 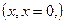 , если x нулевой вектор.
, если x нулевой вектор.
Определение
Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
Длиной (нормой) вектора x в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
 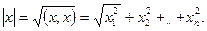
| (1.16.2) |
Имеют следующие свойства длины вектора:
1. 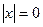 тогда и только тогда, когда
тогда и только тогда, когда  .
.
2. 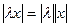 , где λ – действительное число.
, где λ – действительное число.
3. 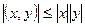 – неравенство Коши–Буняковского.
– неравенство Коши–Буняковского.
4. 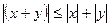 – неравенство треугольника.
– неравенство треугольника.
Угол φ между двумя векторами x и у определяется равенством
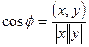
| (1.16.3) |
где 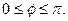
Определение
Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, если два ненулевых вектора ортогональны, то угол между ними равен 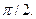
Векторы e1, e2, …, en n –мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. (ei,ej) = 0 при 
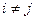 и
и 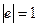 при
при 
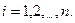 .
.
Теорема
Во всяком n –мерном евклидовом пространстве существует ортонормированный базис.
Упражнения
1. Вычислить определители
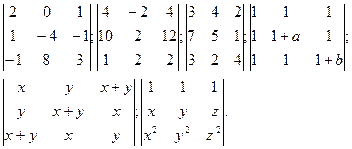
2. Решить системы:




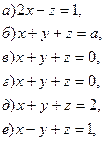
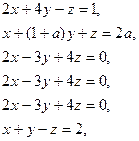

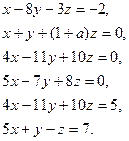
3. Вычислить площадь треугольника с вершинами в точках (1, –2), (2, 3), (4, 5).
4. Лежат ли три точки (1, 1), (3, 3), (0, 0) на одной прямой?
5. Составить уравнение прямой, проходящей через две точки (3, 2) и(–1, 3).
6. Найти высоту треугольника с вершинами А (x 1, y 1), В (x 2, y 2 ), С(x 3, y 3 ).
7. П ользуясь решением предыдущего упражнения, найти площадь треугольника с вершинами А (x1, y1), В (x2, y2 ), С( x3, y3 )
8. Показать, что площадь выпуклого четырехугольника ABCD с вершинами А (x1, y1), В (x2, y2 ), С( x3, y3 ), В( x4, y4 ) равна

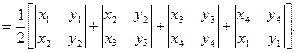
9. Вычислить определитель
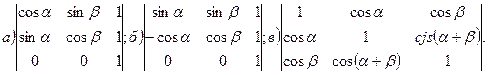
10. Найти х из уравнений:
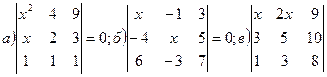


11. При каком порядке обхода вершин выражение в скобках будет иметь знак +?
12. Упростить выражения:
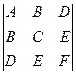
13. Доказать тождество