Задачу определения угла между двумя прямыми мы рассмотрим для случая, когда прямые заданы уравнениями 
и 
. Тогда острый угол между этими прямыми можно определить по формуле:
 .
| (2.9.1) |
Для того, чтобы эти прямые были параллельны, необходимо и достаточно, чтобы выполнялось условие
| (2.9.2) |
Для того, чтобы эти прямые были перпендикулярны, необходимо и достаточно, чтобы имело место соотношение
 или  .
| (2.9.3) |
Пример
Найти угол между прямыми, заданными общими уравнениями 
и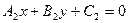 
. Сформулировать условия перпендикулярности и параллельности прямых.
Решение
Если 
, 
– координаты вектора 
, перпендикулярного к первой прямой, а 
, 
– координаты вектора 
, перпендикулярного ко второй прямой, то угол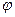 
между векторами и 
определяется по формуле:
 .
| (2.9.4) |
Если прямые параллельны (коллинеарны), то коллинеарны и их нормальные векторы. Следовательно, координаты нормалей и пропорциональны. Таким образом, признаком параллельности данных прямых является условие
 .
| (2.9.5) |
Если прямые перпендикулярны, то перпендикулярны и их нормальные векторы. Скалярное произведение двух перпендикулярных векторов равно нулю. Следовательно, признаком перпендикулярности данных прямых является условие
 =0.
| (2.9.6) |
Пример
Составить уравнение прямой, которая проходит через начало координат и А) параллельна прямой 
Б) перпендикулярна прямой 
В) образует угол 
с прямой 
.
Решение
а) Уравнение прямой, проходящей через начало координат, имеет вид 
. Поскольку параллельные прямые имеют одинаковые угловые коэффициенты, то 
, и уравнение искомой прямой 
.
б) Найдем угловой коэффициент прямой, перпендикулярной данной прямой. Из условия перпендикулярности прямых (2.9.6) следует: 
. Значит, уравнение искомой прямой имеет вид 
.
в) Искомая прямая образует угол 
с прямой . Из формулы (2.9.1) имеем
, или 
, где 
. Решая это уравнение, получим два значения 
и 
. Значит, условию задачи удовлетворяют две прямые: 
и 
.
Пример
Вычислить острый угол между двумя прямыми 
и 
.
Решение
Угловые коэффициенты данных прямых таковы: 
и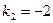 
. Тангенс острого угла между ними определяется по формуле (2.9.1): 
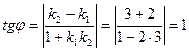. т.е. искомый угол равен .
Расстояние от точки до прямой
Пусть дана прямая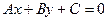 
и точка 
, принадлежащая этой прямой. Получим формулу расстояния от произвольной точки 
до этой прямой.
Рис. 2.8.2
Рассмотрим (Рис. 2.8.2) вектор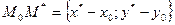 
и вектор нормали 
. Из Рис. 2.8.2 видно, что расстояние 
от точки 
до прямой равно модулю проекции вектора 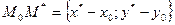на вектор нормали 
:
.
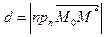Из формулы скалярного произведения следует, что
Так как точка принадлежит прямой, то 
. Следовательно, расстояние от точки 
до прямой равно
 .
| (2.9.7) |
Пример
Две стороны квадрата лежат на прямых 
и 
. Вычислить площадь квадрата.
Решение
Для данных прямых выполнено условие (2.5.5), значит они параллельны и расстояние 
между ними равно стороне квадрата. Возьмем произвольную точку, принадлежащую первой прямой . Положим 
. Найдем 
: 
или 
. Следовательно, точка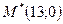 
принадлежит прямой . Найдем расстояние от точки 
до второй прямой по формуле (2.9.7): 
. Следовательно, площадь квадрата равна 
Пример
Найти длину перпендикуляра опущенного из точки 
на прямую 
.
Решение
Воспользуемся формулой (2.6.1), полагая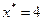 
, 
.
