Глава 1. Линейная алгебра
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики – матричная алгебра. Значительная часть математических моделей объектов и процессов записывается в достаточно простой и компактной матричной форме.
Определение
Матрицей называется совокупность n × m чисел, расположенных в виде таблицы, содержащей n строк и m столбцов.
Общее обозначение
 . .
| (1.1.1) |
Числа aik (i = 1, 2, …, n; k = 1, 2, …, m), составляющие матрицу, называются ее элементами. Первый индекс обозначает номер строки, а второй – номер столбца.
Если матрица имеет n строк и m столбцов, то говорят, что матрица имеет размерность n ´ m.
Матрица, все элементы которой равны нулю, называется нулевой.
Для матриц одинаковой размерности устанавливается понятие их равенства: две матрицы равны тогда и только тогда, когда равны их соответствующие элементы.
Матрица, состоящая из одной строки, называется матрицей (вектором) – строкой, а из одного столбца – матрицей (вектором) – столбцом. Например,
 – матрица–строка,
– матрица–строка,
 – матрица–столбец.
– матрица–столбец.
Если n = m, то матрица называется квадратной.
Квадратную матрицу, содержащую n строк и n столбцов, называют матрицей n–го порядка.
Квадратная матрица, у которой равны нулю все элементы, кроме, может быть, элементов стоящих на главной диагонали, называется диагональной.
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной и обозначается E.
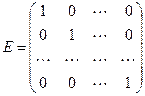 . .
| (1.1.2) |
Транспонированием матрицы A называется перемена местами строк и столбцов матрицы с сохранением их номеров. Полученная таким образом матрица называется транспонированной и обозначается A *.
Пример
 ,
,  .
.
Ясно, что (A *)* = A. Матрица, совпадающая со своей транспонированной (A * = A), называется симметрической.
Действия над матрицами
1. Сложение матриц.
Пусть
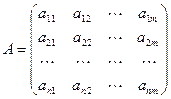 ; ;  . .
| (1.2.1) |
Суммой двух матриц A и B одинаковой размерности называется матрица C = A + B той же размерности, элементы которой равны сумме соответствующих элементов матриц A и B, т.е.
 . .
| (1.2.2) |
Пример
 ,
,  ,
,  .
.
2. Умножение матрицы на число.
Произведением матрицы A на число l называется матрица C = l A, элементы которой равны элементам матрицы A, умноженным на число l, т.е.
 , (i = 1, 2, …, n; k = 1, 2, …, m). , (i = 1, 2, …, n; k = 1, 2, …, m).
| (1.2.3) |
Матрица – A = (–1)× A называется противоположной матрице A. Очевидно, что A + (– A) = 0, где 0 – нулевая матрица той же размерности, что и матрица A.
Легко проверить, что операции сложения матриц и умножения матрицы на число, называющиеся линейными операциями, обладают следующими свойствами:
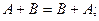
| (1.2.4) |

| |

| |

| |

| |

| |

| |

|
3. Вычитание матриц.
Разностью матриц A и B одинаковой размерности называется такая матрица C = A – B, сумма которой с матрицей B равна матрице A.

| (1.2.5) |
Чтобы получить матрицу C = A – B, достаточно из элементов матрицы A вычесть соответствующие элементы матрицы B:
 (i = 1, 2, …, n; k = 1, 2, …, m). (i = 1, 2, …, n; k = 1, 2, …, m).
| (1.2.7) |
4. Умножение матриц.
Произведением двух матриц A и B, заданных в указанном порядке, называется такая матрица С = A × B, каждый элемент которой cik равен сумме произведений элементов i –ой строки матрицы A на соответствующие элементы k –го столбца матрицы B.
Матрицы A и B можно перемножить, если количество элементов в строке матрицы A равно количеству элементов в столбце матрицы B.
Пример
 ;
;  . Найти A × B.
. Найти A × B.
Решение
 .
.
Замечание
Произведение матриц BA рассмотренных в приведенном выше примере, не существует, т.к. число столбцов (2) матрицы B (первого множителя) не равно числу строк (3) матрицы A (второго множителя).
Пример

 Найти A × B и B × A.
Найти A × B и B × A.
Решение
 ,
,  .
.
Как видим из примера, A × B ¹ B × A, т.е. произведение матриц не обладает коммутативным свойством.
Свойства произведения матриц:

| (1.2.8) |
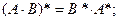
| |

| |

| |

| |

|
1.3. Определители 2–го и 3–го порядков
Квадратной матрице можно поставить в соответствие число, называемое определителем этой матрицы.
Пусть A – матрица 2–го порядка:
 . .
| (1.3.1) |
Определителем или детерминантом матрицы A 2–го порядка называется число, определяемое по формуле:

| (1.3.2) |
Пусть дана матрица 3–го порядка:

| (1.3.3) |
Определителем матрицы A 3–го порядка называется число, определяемое по формуле:


| (1.3.4) |
Пример
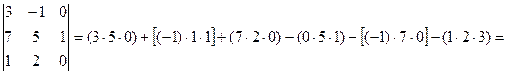

Свойства определителей
Свойство 1
При транспонировании матрицы ее определитель не изменяется, т. е.:
| det A * = det A | (1.4.1) |
Свойство 2
При перестановке двух параллельных рядов (строк либо столбцов) матрицы знак ее определителя изменяется на противоположный. Абсолютное значение определителя при этом не меняется.

| (1.4.2) |
Свойство 3
Определитель, содержащий два одинаковых ряда, равен нулю:

| (1.4.3) |
Свойство 4
Определитель, содержащий ряд из нулей, равен нулю:

| (1.4.4) |
Свойство 5
Общий множитель всех элементов одного ряда определителя можно вынести за знак определителя:
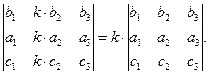
| (1.4.5) |
Свойство 6
Если все элементы какого–либо ряда определителя представлены в виде суммы двух слагаемых, то такой определитель можно представит в виде суммы двух определителей, у которого элементы рассматриваемого ряда равны соответствующим слагаемым. А остальные элементы у всех трех определителей одни и те же:
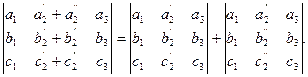
| (1.4.6) |
Свойство 7
Определитель не изменится, если к элементам какого–либо его ряда прибавить соответствующие элементы параллельного ему ряда, умноженного на одно и то же число:

| (1.4.7) |
Свойство 8
Определитель не изменится, если к элементам какого–либо ряда прибавить соответствующие элементы параллельного ему ряда, умноженные на одно и то же число.

| (1.4.8) |
Минором Mik элемента aik определителя называется определитель, который получается из данного после вычеркивания i –ой строки и k –го столбца, на пересечении которых стоит этот элемент.
Пример
 Найти миноры Mik.
Найти миноры Mik.
Решение
Минор M 11 элемента a 11=5 равен: 
Минор M 32 элемента a 32=–1 равен: 
Алгебраическим дополнением Aik элемента aik определителя называется минор этого элемента, взятый со знаком “+”, если i + k – четное число, и со знаком “–“, если i + k – нечетное число, т.е.
| Aik =(–1) i + k Mik. | (1.4.9) |
Пример
A 11 = (–1)1+1 M 11 = M 11, A 12 = (–1)1+2 M 12 = – M 12, A 32 = (–1)3+2 M 32 = – M 32 и т.д.
Свойство 9
Определитель равен сумме произведений элементов какого–либо его ряда на их алгебраические дополнения, т.е. детерминант матрицы (1.3.3) равен
| det A = a 11 A 11 + a 12 A 12 + a 13 A 13; det A = a 12 A 12 + a 22 A 22 + a 23 A 23 и т.д. | (1.4.10) |
Пример
Вычислить определитель матрицы: 
Решение
det A = a 11 A 11 + a 12 A 12 + a 13 A 13.

Итак, det A = 3×7 + (–2) ×(–10) + 0×(–5) = 41.
Свойство 10
Сумма произведений элементов какого–либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ему ряда равна нулю:
| a 11 A 21 + a 12 A 22 + a 13 A 13 = 0, a 11 A 13 + a 21 A 23 + a 31 A 33 = 0 и т.д. | (1.4.11) |
Определители высших порядков
Введем понятие определителя n –го порядка.
Определение
Определителем матрицы A n –го порядка называется алгебраическая сумма n! произведений n –го порядка элементов этой матрицы, причем в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы.
Заметим, что с ростом n резко увеличивается число членов определителя (n!). Например, для n = 4 определитель содержит 24 слагаемых. Поэтому на практике при вычислении определителей высоких порядков используют другие формулы.
Свойстваопределителей, рассмотренные в разделе 4, справедливы и для определителей любого порядка. Поэтому для вычисления определителей 4–го, 5–го и более высоких порядков можно воспользоваться свойством9, сформулированное в общем случае определителя произвольного порядка носит название теоремы Лапласа. Как нетрудно убедиться, вычисление определителя 4–го порядка сводится к вычислению четырех определителей 3–го порядка. Для облегчения решения этой задачи определитель преобразуют, используя свойство 8, стремясь получить в одном из рядов максимальное число нулей.
Теорема (Теорема Лапласа)
Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
 
| (1.5.1) |
Формула (1.5.1) называется разложением определителя по i–ой строке. Аналогичное утверждение имеет место и для разложения по любому столбцу.
Определение
Квадратная матрица называется вырожденной если ее определитель равен нулю.
Пример
Вычислить определитель матрицы A 4–го порядка:

Решение
По свойству 9 вычислим det A, разлагая его, например, по элементам 3–го столбца:

Преобразуем детерминант следующим образом: умножим 2–ю строку на 2 и прибавим к 3–й строке; умножим 2–ю строку на –6 и прибавим к 4–й строке. Получаем


Обратная матрица
Пусть дана квадратная матрица А:

| (1.6.1) |
Определение
Матрица B называется обратной к матрице A, если A × B = B × A = E, где E – единичная матрица.
Матрица, обратная к A, обозначается A –1.
Можно доказать, что, если det A ¹ 0, то матрица A имеет обратную матрицу A –1, определяемую по формуле:

| (1.6.2) |
где Aik – алгебраические дополнения к элементу aik матрицы A (i, k = 1, 2, …, n). Построение обратной матрицы можно описать так:
1. Составим матрицу A ’, написав на месте каждого элемента матрицы A его алгебраическое дополнение.
2. Разделим каждый элемент A ’ на det A.
3. Транспонируем полученную матрицу.
Пример
Найти матрицу, обратную к матрице:

Решение
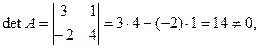
следовательно матрица A –1, обратная данной существует.

Разделим элементы матрицы A ’ на det A и транспонируем, получаем:

A 11 = 4, A 12 = –(–2) = 2, A 21 = –1, A 22 = 3. Окончательно,

Проверка:


Матрица A –1 найдена верно.
Ранг матрицы
Рассмотрим прямоугольную матрицу (1.1.1), содержащую n строк и m столбцов. Выделим в ней произвольным образом квадратную матрицу k –го порядка. Определитель этой матрицы называется минором k –го порядка матрицы А. Очевидно, что в общем случае таких миноров k –го порядка может быть несколько, а максимальный порядок миноров равен минимальному из чисел m и n, т. е. k £ min(n; m). Далее, из всех возможных миноров матрицы А выделим те из них, которые отличны от нуля. В свою очередь, среди этих миноров можно найти по крайней мере один минор наибольшего порядка.
Определение
Наибольший порядок отличных от нуля миноров называется рангом матрицы А. Ранг матрицы обозначается rang A или r(A).
Из определения следует:
1.Ранг матрицы A не превосходит меньшего из ее размеров, т.е. k £ min(n; m).
2.Ранг матрицы равен нулю тогда, когда все элементы матрицы равны нулю, т.е. A =0.
3.Для квадратной матрицы n –го порядка r (A) = n тогда и только тогда, когда матрица A – невырожденная.
Пример
Вычислить ранг матрицы

Решение
Матрица A имеет размер 4´3, поэтому rang A £ 3. Однако, все определители матрицы A равны нулю. Следовательно, rang A £ 2. Нетрудно видеть, что максимальный порядок миноров этой матрицы, отличных от нуля, равен 2.
Определение
Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы. Столбцы и строки этой матрицы, участвующие в образовании базисного минора, также называются базисными.
Пример
Вычислить ранг матрицы

Решение
Матрица A имеет четвертый порядок, поэтому r (A) £ 4. Однако |A| = 0, так как матрица A содержит нулевой столбец, поэтому r (A) £ 3. Все подматрицы третьего порядка тоже содержат нулевой столбец и поэтому имеют нулевые определители значит r (A) £ 2. Все подматрицы второго порядка либо имеют нулевой столбец (второй или четвертый), либо имеют пропорциональные столбцы (первый и третий), поэтому тоже имеют нулевые определители; таким образом r (A) £ 1. Поскольку матрица A содержит ненулевые элементы, т.е. невырожденные подматрицы первого порядка, то r (A) = 1.
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются перечисленные ниже элементарные преобразования, сохраняющие ранг матрицы.
1. Отбрасывание нулевой строки (столбца).
2. Умножение всех элементов строки (столбца) на число, не равное нулю.
3. Изменение порядка строк (столбцов), а также прибавление к каждому элементу одной строки (столбца) линейной комбинации соответствующих элементов другой строки (столбца).
4. Транспонирование матрицы.
Теорема
Ранг матрицы не изменится при элементарных преобразованиях.
1.8. Системы линейных алгебраических уравнений.
Основные понятия и определения
Определение
Система уравнений вида
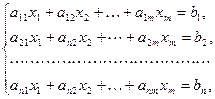
| (1.8.1) |
называется системой n линейных уравнений с m неизвестными x 1, x 2, … xm. Здесь aij и bj (i = 1, 2, …, n; j = 1, 2, …, m) – произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений (1.8.1).
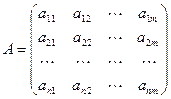
| (1.8.2) |
называется основной матрицей системы.
Система уравнений, все свободные члены bi (i = 1, 2, …, n) которой равны нулю, называется однородной.
Решением системы называется такая совокупность значений неизвестных x 1 = a1, x 2 = a2, …, x m = am, при подстановке которых в систему (1.8.1) каждое из ее уравнений обращается в верное равенство.
Определение
Система уравнений, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.
Пример
Система уравнений  – совместная и определенная, так как имеет единственное решение. Система уравнений
– совместная и определенная, так как имеет единственное решение. Система уравнений  – несовместная, а система уравнений
– несовместная, а система уравнений  – совместная и неопределенная, так как имеет бесконечное множество решений.
– совместная и неопределенная, так как имеет бесконечное множество решений.
Однородная система имеет по крайней мере одно решение – нулевое:
| x 1 = 0, x 2 = 0, …, xm = 0. | (1.8.3) |
Решить систему уравнений – значит найти ее решение или доказать, что система решений не имеет.
1.9. Системы n линейных уравнений с n неизвестными. Формулы Крамера
Рассмотрим систему уравнений, у которой число уравнений совпадает с числом неизвестных (n = m):
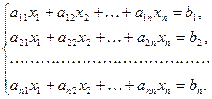
| (1.9.1) |
Предположим, что определитель основной матрицы системы (или главный определитель системы) отличен от нуля:
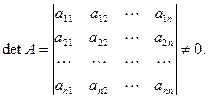
| (1.9.2) |
Можно доказать, что такая система уравнений имеет единственное решение, определяемое по формулам, называемым формулами Крамера:
 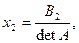 
| (1.9.3) |
Где
  …, …, 
| (1.9.4) |
Матрицы Bi (i = 1, 2, …, n) получаются из матрицы A заменой i –го столбца столбцом свободных членов.
Пример
Решить систему уравнений с помощью формул Крамера:

Решение
Вычислим главный определитель системы:


Теперь вычислим определители матриц B 1, B 2, B 3:



Применяя формулы Крамера для определения решений, получаем:



Проверкой можно убедиться в верности найденного решения.






