Решение:
Обозначим через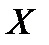 
сумму числа очков, которые выпадут на всех гранях, через 
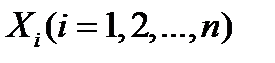– число выпавших очков на грани 
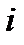-й кости. Тогда, очевидно,
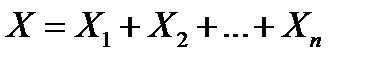
Следовательно,
(*)
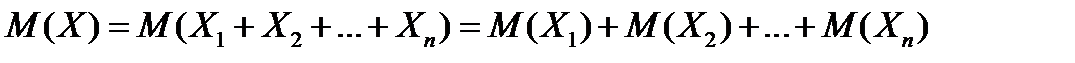Очевидно, все величины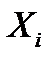 
имеют одинаковое распределение, а, следовательно, одинаковые числовые характеристики и, в частности, одинаковые математические ожидания, т.е.
.
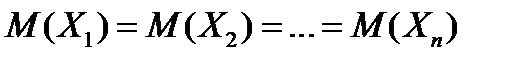В силу (*) получим
(**)
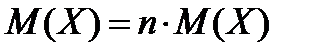Таким образом, достаточно вычислить математическое ожидание величины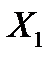 
,т.е. математическое ожидание числа очков, которые могут выпасть на первой кости. Для этого напишем закон распределения 
:
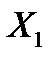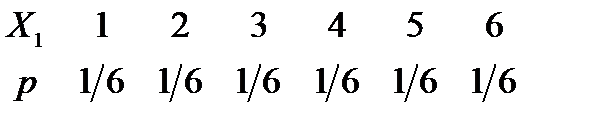
Найдем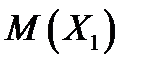 
(***)
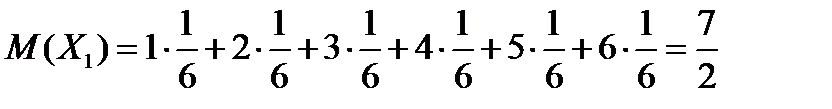Подставив (***) в (**), окончательно получим
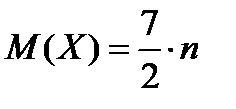
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится пять изделий. Найти математическое ожидание дискретной случайной величины X — числа партий, в каждой из которых окажется ровно четыре стандартных изделия,— если проверке подлежит 50 партий.
Решение:
Математическое ожидание дискретной случайной величины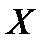 
равно произведению числа испытаний на вероятность появления события.
В данном случае можно использовать формулу Бернулли
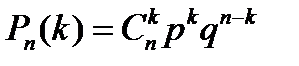
В данной задаче, по условию,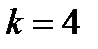 
, 
, 
, 
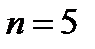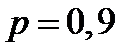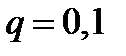
Находим вероятность
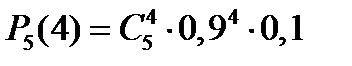
Так как проверяется 50 партий, то найденную вероятность нужно умножить на 50
Получаем
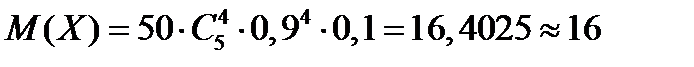
№201 Доказать:
1), если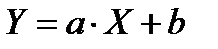 
;
2) 
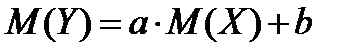
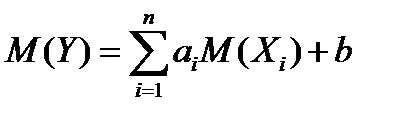, если 
.
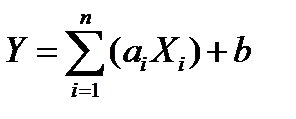Решение:
1) 
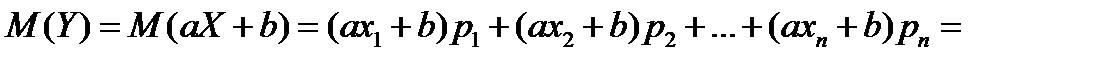
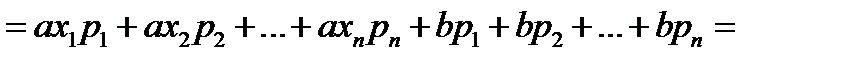
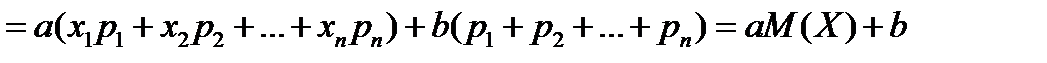
Что и требовалось доказать.
2) 
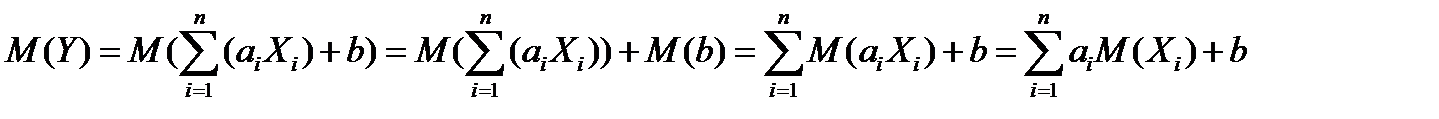Что и требовалось доказать.
№202 События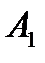 
, 
,…, 
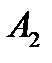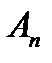несовместны и образуют полную группу; вероятности появления этих событий соОтветственно равны 
, 
,…, 
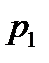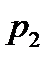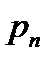. Если в итоге испытания появляется событие 
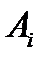(i=1, 2, …,n), то дискретная случайная величина 
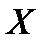принимает возможное значение 
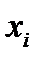, равное вероятности 
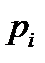появления события 
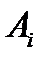. Доказать, что математическое ожидание случайной величины 
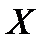имеет наименьшее значение, если вероятности всех событий одинаковы.
Решение:
Возможные значения величины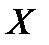 
по условию равны вероятности 
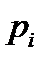событий 
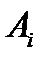; вероятность возможного значения 
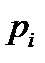, очевидно, также равна 
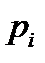. Таким образом, 
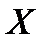имеет следующее распределение:
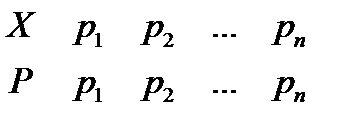
Найдем математическое ожидание:
(*)
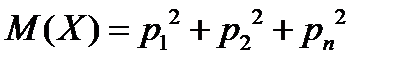Рассматриваемые события образуют полную группу, поэтому:
.
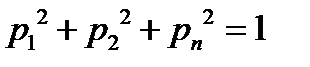Из дифференциального исчисления известно, что если сумма независимых переменных постоянна, то сумма квадратов этих переменных имеет наименьшее значение в случае равенства переменных. Применительно к рассматриваемой задаче это означает: сумма (*), т. е. математическое ожидание М (X), имеет наименьшее значение, если вероятности всех событий, образующих полную группу, равны между собой, что и требовалось доказать.
