)=0,4895
Следовательно, 2Ф=2*0,4895=0,979
Ответ: 0,979
№134 Французский ученый Бюффон бросил монету 4040 раз, причем «герб» появился 2048 раз. Найти вероятность того, что при повторении опыта Бюффона относительная частота появления «герба» отклониться от вероятности появления «герба» по абсолютной величине не более чем в опыте Бюффона.
Решение:
n=4040; k=2048; p=0,5
Воспользуемся формулой 
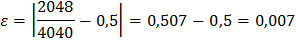
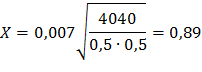
Ф(0,89) = 0,3133
2Ф(0,89) = 0,6296
Ответ: 0,6296
№135 Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний n, при котором с вероятностью 0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
Решение:
По условию, р = 0,5; q = 0,5; ε=0,02;
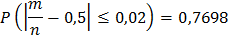
Воспользуемся формулой
В силу условия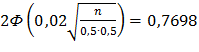 
Или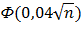 
=0,3849
По таблице приложения 2 найдем Ф(1,2) = 0,3849.
Следовательно, 0,04 
= 1,2 или = 30
Таким образом, искомое число испытаний n =900.
Ответ: 900
№136 Сколько раз нужно бросить игральную кость, чтобы вероятность неравенства
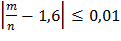была не меньше чем вероятность противоположного неравенства, где m—число появлений одного очка в n бросаниях игральной кости?
Решение:
Воспользуемся формулой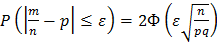 
По условию, р=1/6, q = 5/6, ε = 0,01.
Вероятность осуществления неравенства, противоположного заданному,
т.е. неравенства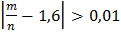 
, равна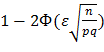 
Согласно условию должно иметь место неравенство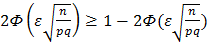 
или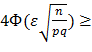 
1,
отсюда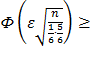 
0,25 (*)
По таблице приложения 2 найдем Ф(0,67) =0,2486; Ф(0,68) = 0,2517.
Выполнив линейную интерполяцию, получим Ф (0,6745) =0,25.
Учитывая соотношение (*) и принимая во внимание, что функция Ф (x)— возрастающая, имеем
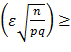0,6745 или 0,01 
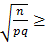0,6745
Отсюда искомое число бросаний монеты n≥632.
Ответ: n>=632
№137 Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти наименьшее число испытаний n, при котором с вероятностью 0,99 можно ожидать, что относительная частота появлений события отклонится от его вероятности по абсолютной величине
не более чем на 0,04.
Решение:
По условию, р = 0,2; q = 0,8; ε=0,04;
Воспользуемся формулой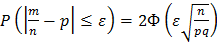
Получим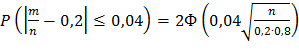 
0,99 или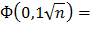 
0,495.
По таблице приложения 2 найдем Ф(2,56) =0,4948; Ф(2,58) = 0,4951
Выполнив линейную интерполяцию, получим Ф (2,573) =0,495.
Следовательно, 0,01 =2,573
Отсюда n=661
Ответ:661
№138 В урне содержатся белые и черные шары в отношении 4:1. После извлечения шара регистрируется его цвет, и шар возвращается в урну. Чему равно наименьшее число извлечений n, при котором с вероятностью 0,95 можно ожидать, что абсолютная величина отклонения относительной частоты появления белого шара от его вероятности будет не более чем 0,01?
Решение:
По условию p=1/5; q=4/5; ε=0,01; P=0,95;
Воспользуемся формулой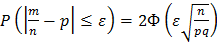
Из условия P=0.95=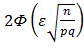 
, отсюда Ф=0,475
0,475=Φ(x)=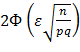 
,
Φ=0,475 соответствует значение x=1,95 (из Приложения 2),
Тогда x=1.9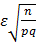5= 
= 
=0,025
n=6147
Ответ: 6147
№139 Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число ε, чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превысила ε.
Решение:
Воспользуемся формулой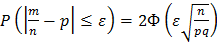
По условию, n=400, p=0,8, q=0,2, P=0,99
Следовательно,
0,99
2Ф(50ε) = 0,99
Ф(50ε)=0,495
По таблице приложения 2 найдём Ф(2,57) = 0,495,
значит 50ε = 2,57
ε = 0,05
Ответ: 0,05
№140 Вероятность появления события в каждом из 900независимых испытаний равна 0,5. Найти такое положительное число ε, чтобы с вероятностью 0,77 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,5 не превысила ε.
Решение:
Воспользуемся формулой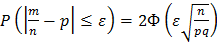
По условию,n=900; p=0,5; q=0,5; P=0,77.
Следовательно,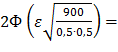 
0,77
Ф(60ε)=0,385
По таблице приложения 2 найдем Ф(1,20) = 0,385, значит 60ε=1,20.
Отсюда искомое число ε = 0,02.
Ответ: 0,02
№141 Вероятность появления события в каждом из 10 000 независимых событий равна 0,75. Найти такое положительное число ε, чтобы с вероятностью 0,98 абсолютная величина отклонения относительной частоты появления события от его вероятности 0,75 не превысила ε.
Решение:
Воспользуемся формулой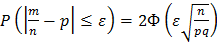
По условию, n = 10000, p = 0,75, q = 0,25.
Следовательно,
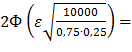0,98 или Ф(231ε) = 0,49.
Т.к. Ф(2,34) = 0,49, значит 231ε = 2,34. Отсюда искомое число ε = 0,01.
Ответ: 0,01
№142 Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятность 0,95 границы, в которых будет заключено число m стандартных деталей среди проверенных.
Решение:
Воспользуемся формулой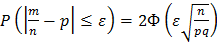
По условию, n=900, p=0,9, q=0,1.
Следовательно,
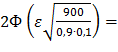0,95
2Ф(100ε) = 0,95
Ф(50ε) = 0,475
По таблице приложения 2 найдём Ф(1,96) = 0,475, значит 100ε = 1,96.
Отсюда ε≈0,02
Таким образом, с вероятностью 0,95 отклонение относительной частоты стандартных деталей от вероятности 0,9 удовлетворяет неравенству
0,02
0,88 ≤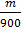 
≤ 0,92
Отсюда искомое число m стандартных деталей среди 900 проверенных с вероятностью 0,95 заключено в границах [792; 828].
Ответ: 792≤m≤828
Митько Дмитрий
№143 Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,95 границы, в которых будет заключено число m бракованных изделий среди проверенных.
Решение:
По условию, n=475, p=0,05, q=0,95. Следовательно,
По таблице приложения 2 найдём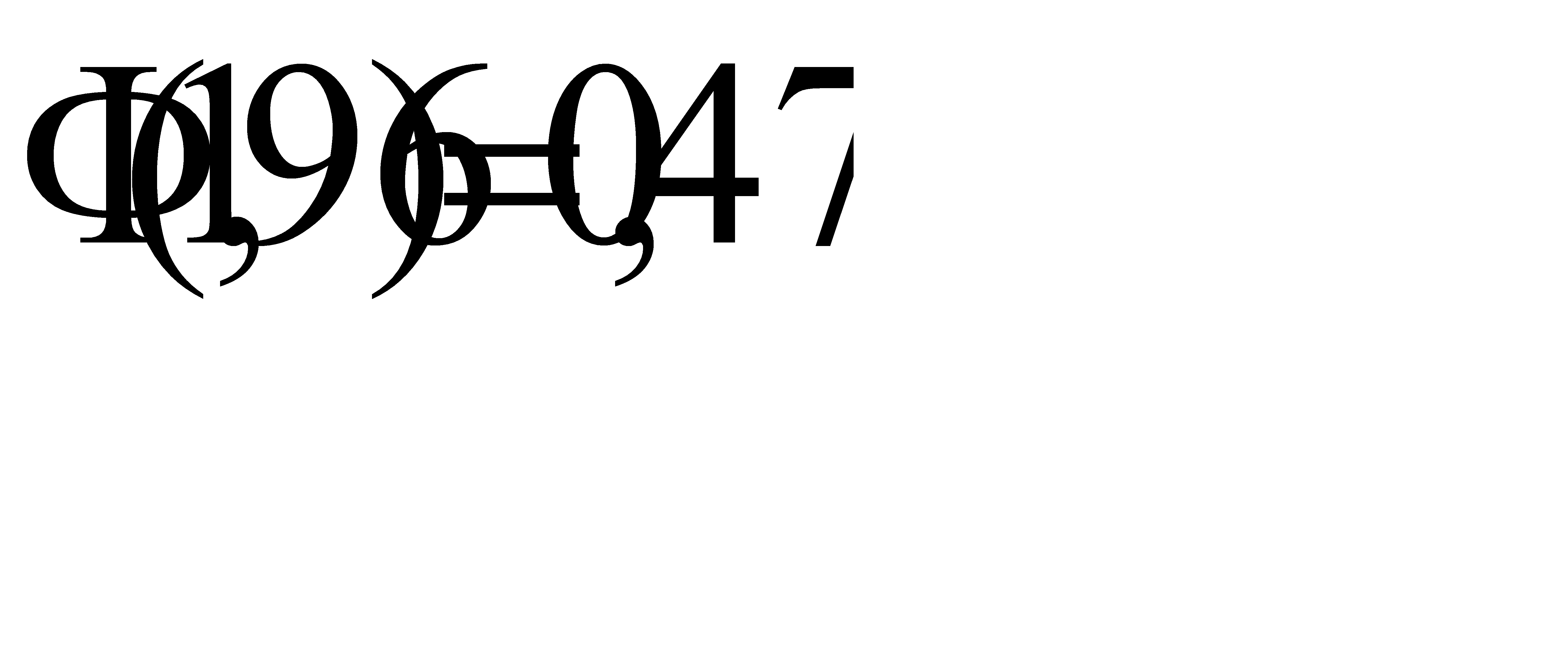 
, значит 
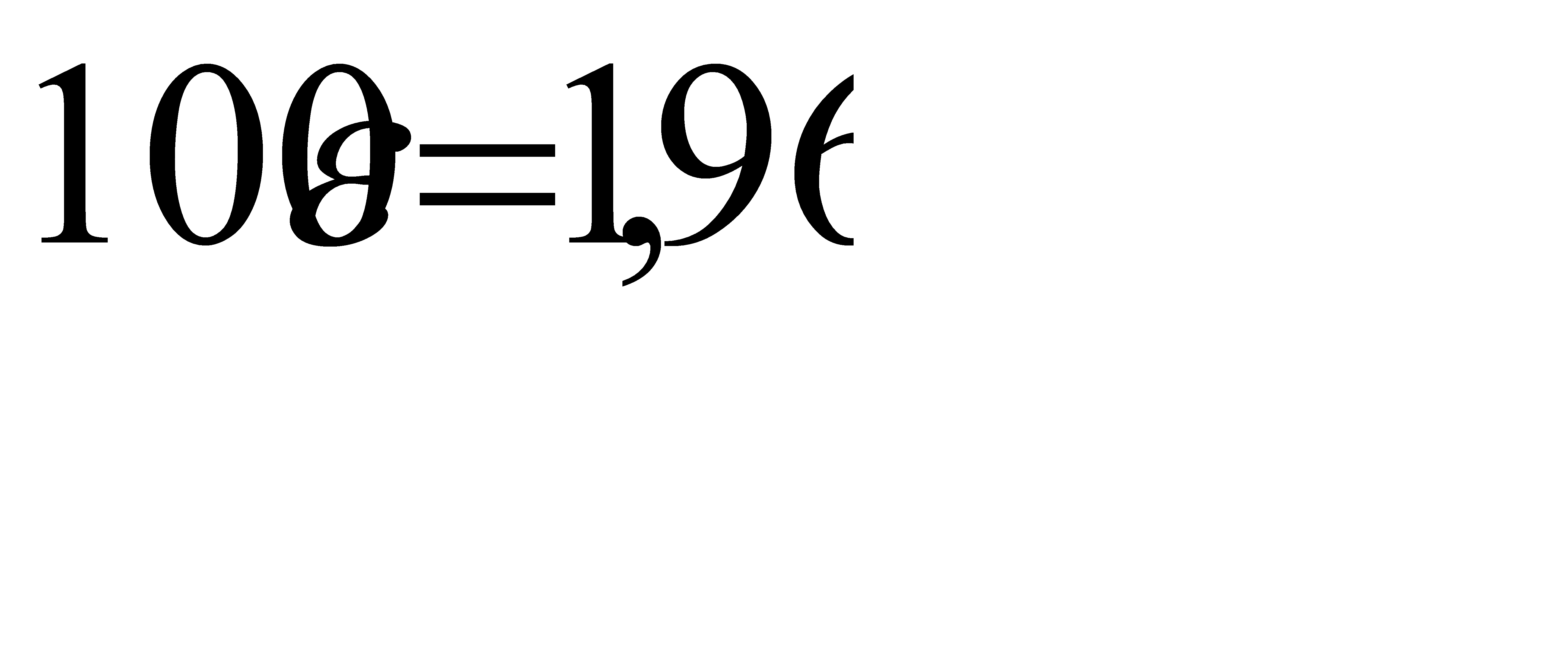. Отсюда 
.
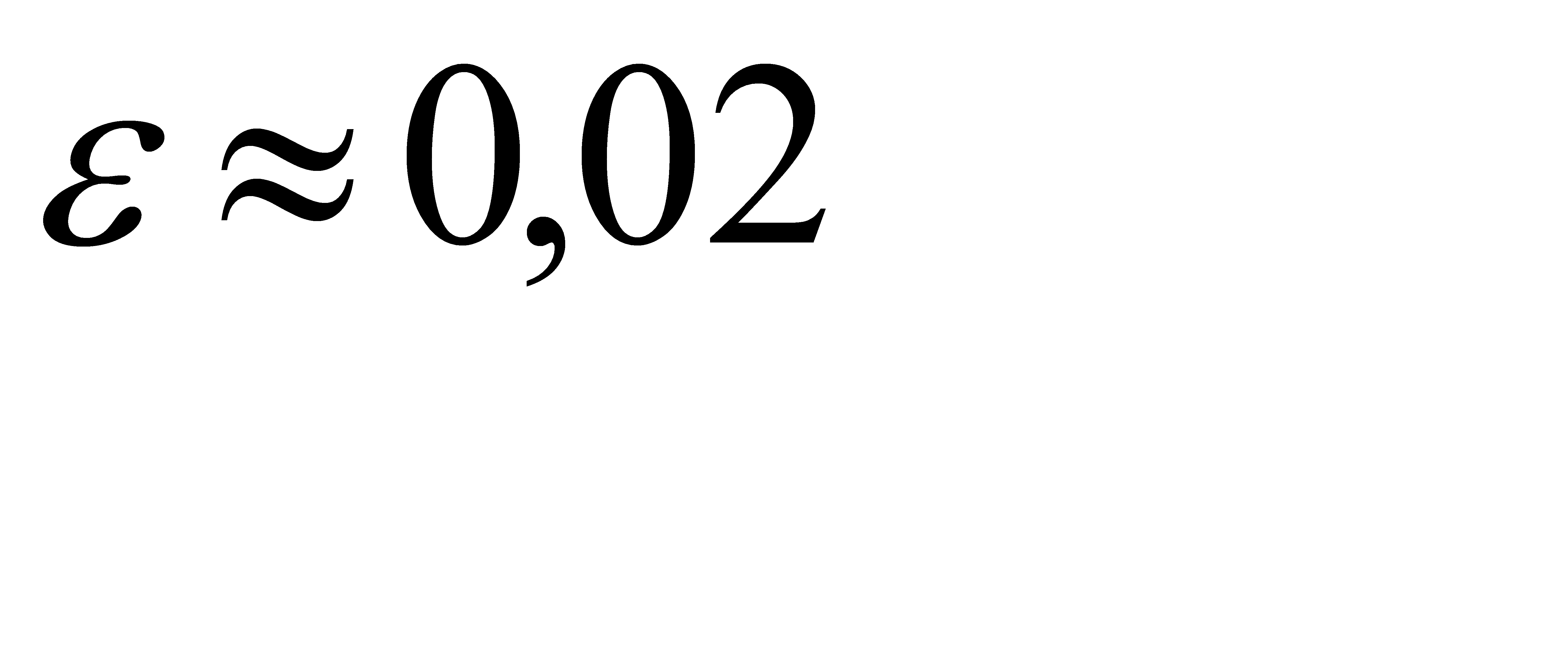Таким образом, с вероятностью 0,95 отклонение относительной частоты бракованных изделий от вероятности 0,05 удовлетворяет неравенству
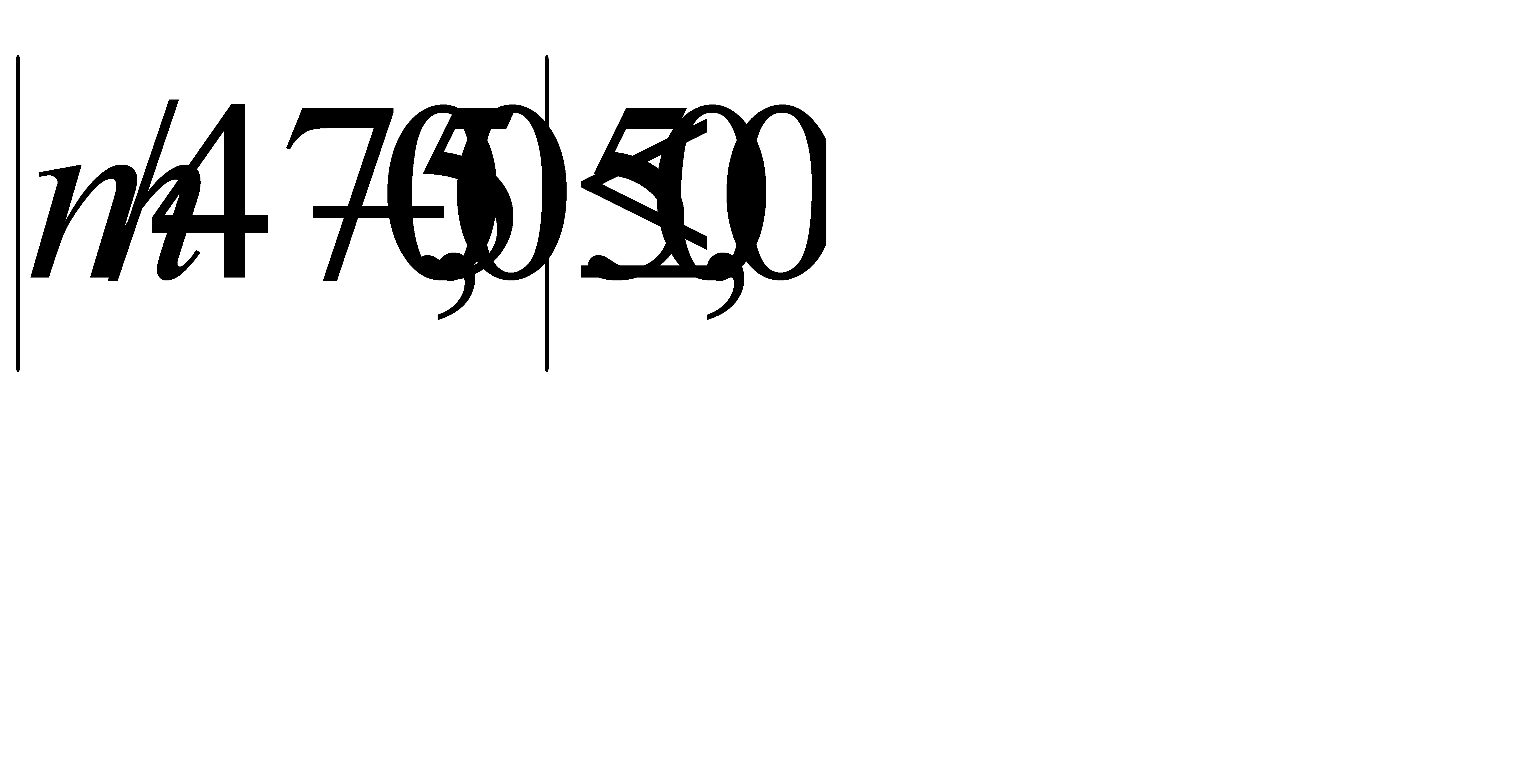
Отсюда искомое число m бракованных изделий среди 475 проверенных с вероятностью 0,95 заключено в следующих границах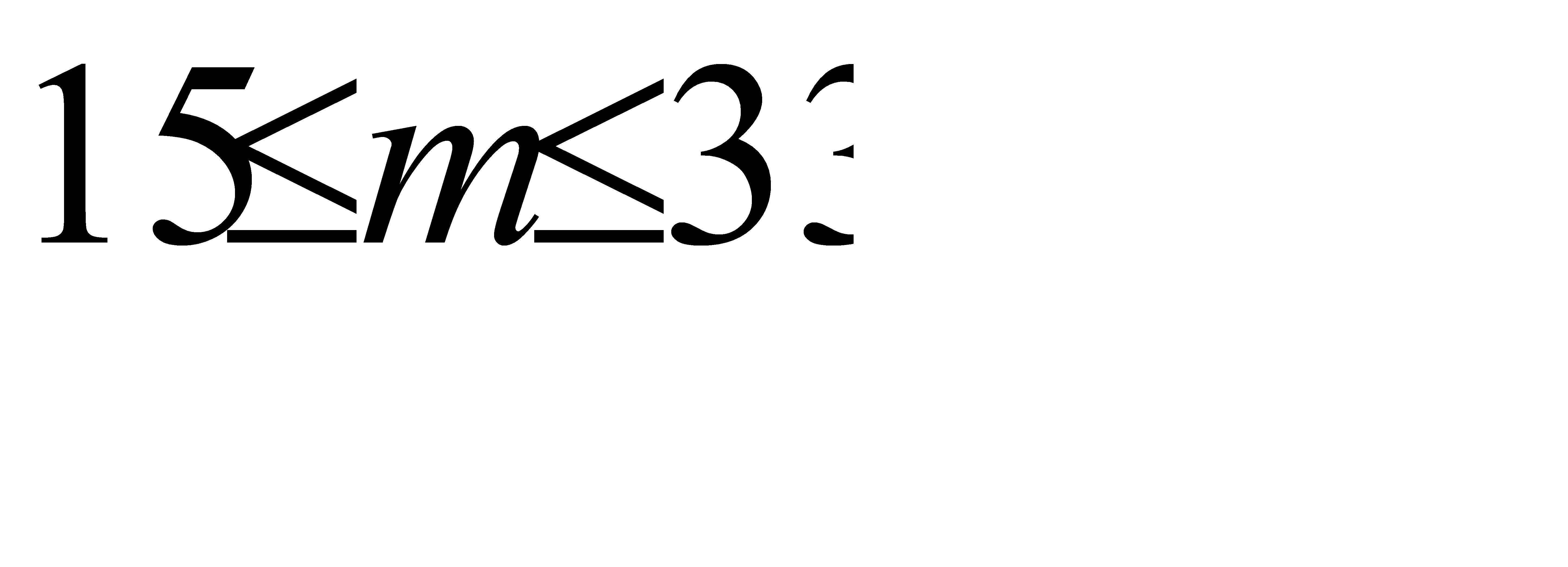 
.
Ответ: .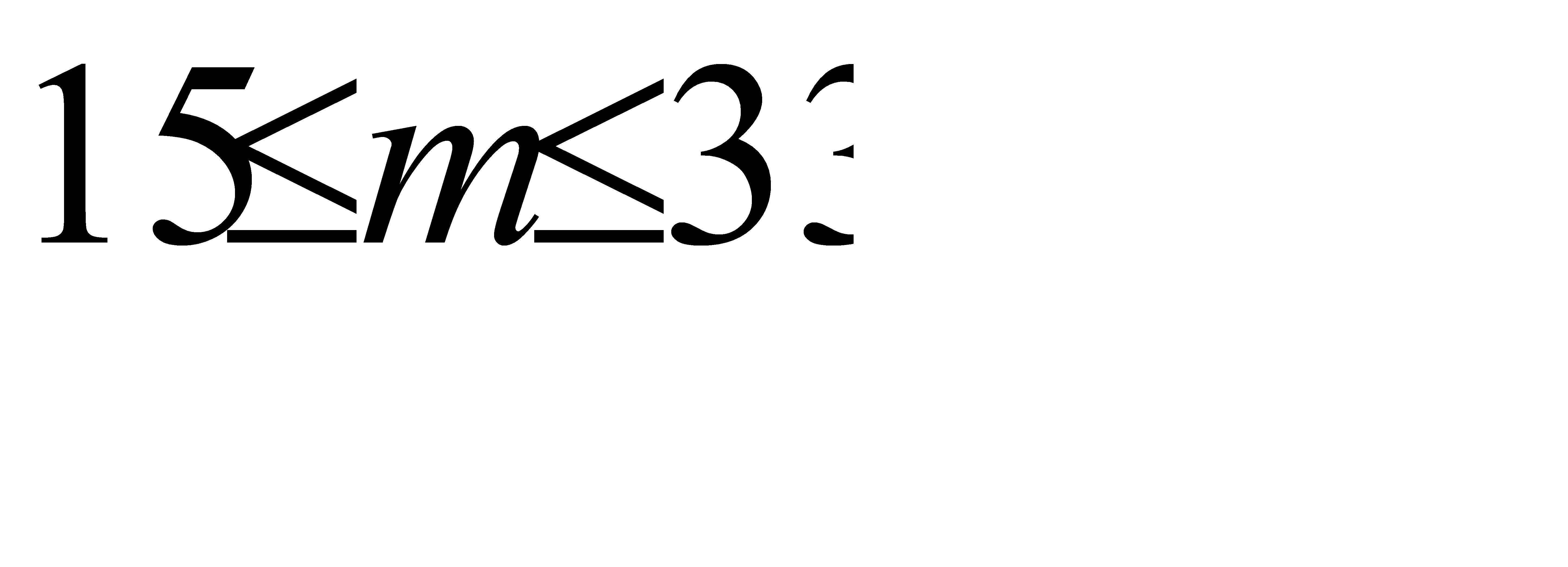
№144 Игральную кость бросают 80 раз. Найти с вероятностью 0,99 границы, в которых будет заключено число m выпадений шестёрки.
Решение:
По условию, n=80, p=1/6, q=5/6. Следовательно,
По таблице приложения 2 найдём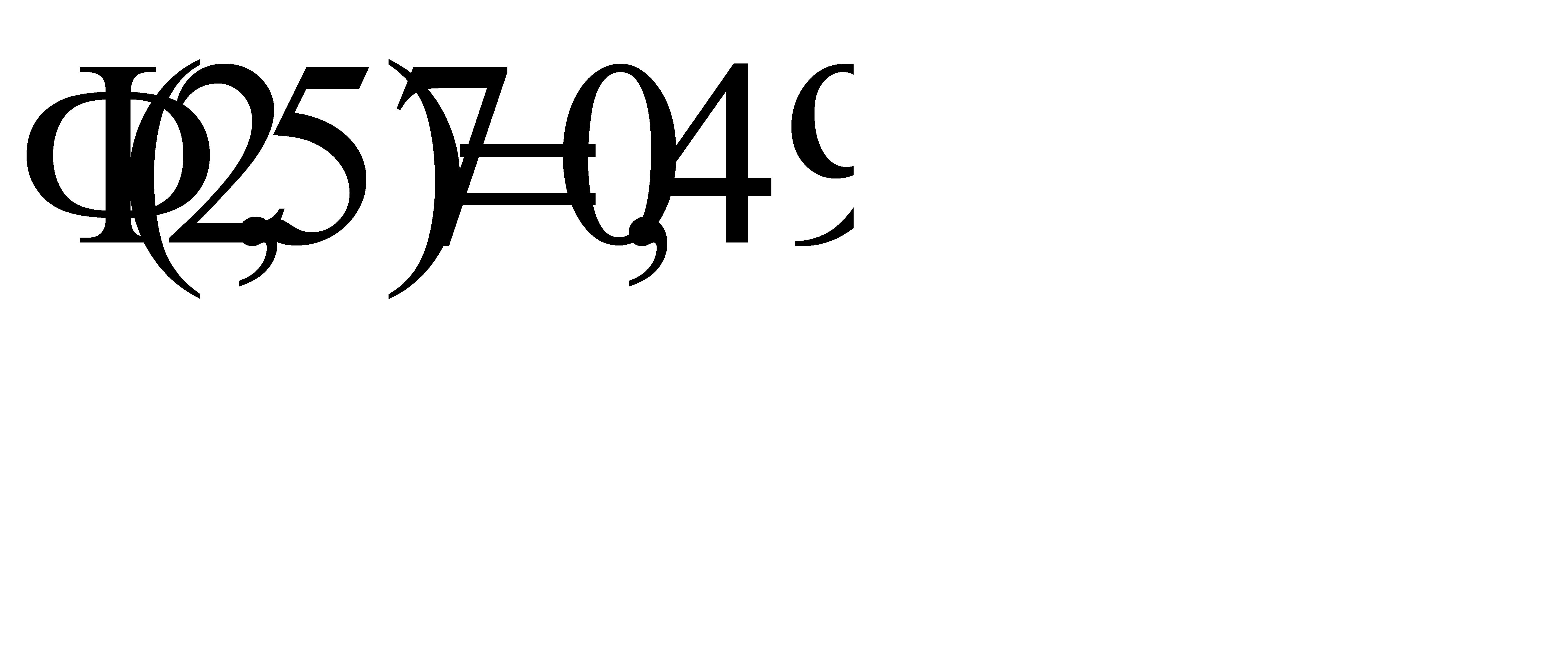 
, значит 
. Отсюда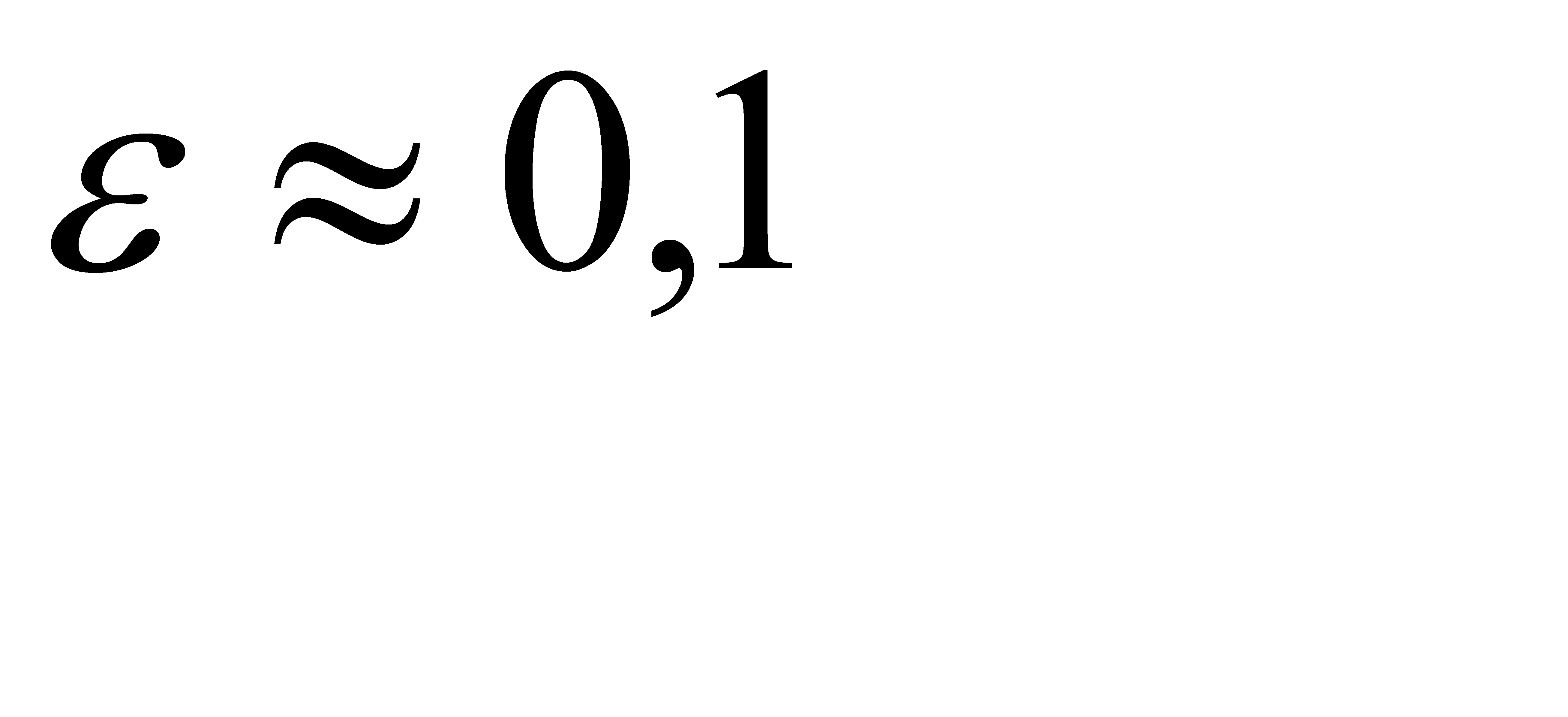 
.
Таким образом, с вероятностью 0,99 отклонение относительной частоты выпадения шестёрки от вероятности 1/6 удовлетворяет неравенству
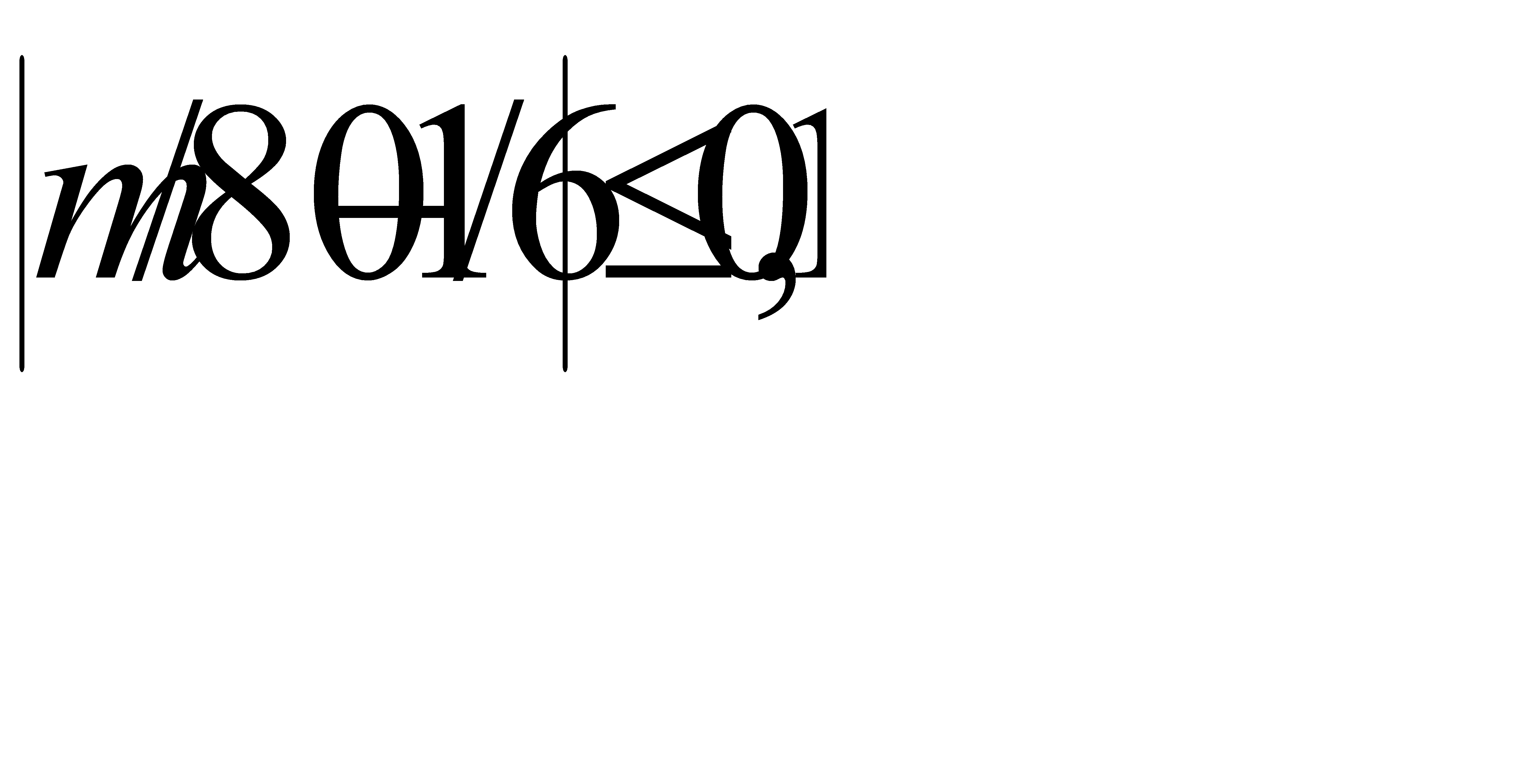
Отсюда искомое число m испытаний среди 80 с вероятностью 0,99 заключено в следующих границах 
.
Ответ: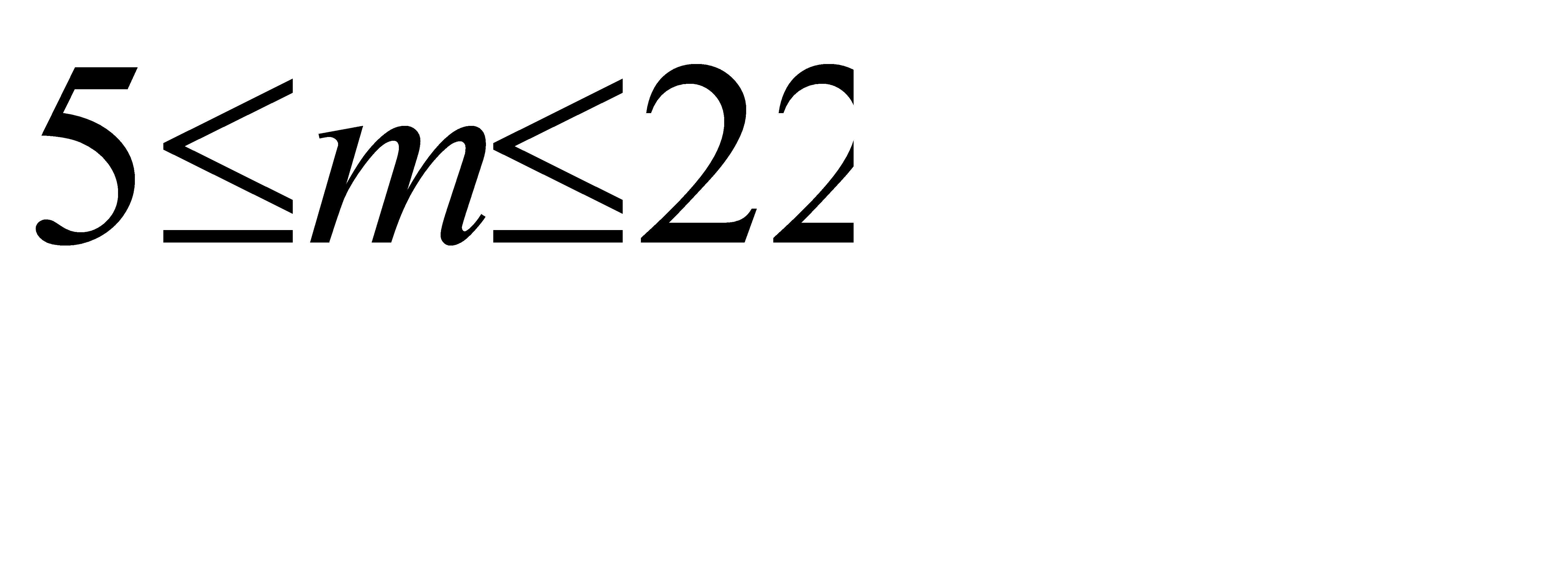 
.
№145 Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание.
Решение:
По условию, n=15, q=0.9, p=0.1. Найдем наивероятнейшее число k0 из двойного неравенства:
Подставив данные задачи, получим:
Так как 
– целое число и поскольку между числами 13.4 и 14.4 заключено одно целое число, а именно 14, то искомое наивероятнейшее число 
№146 Отдел технического контроля проверяет партию из 10 деталей. Вероятность того, что деталь стандартна, равна 0,75. Найти наивероятнейшее число деталей, которые будут признаны стандартными.
Решение.
По условию n=10; p=0,75; q=1-p=0,25. Найдем наивероятнейшее число деталей из неравенства:
Подставив значение получим:
Только одно целое число удовлетворяет неравенству. Это число 8. 
№147 Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годными к продаже.
Решение.
По условию, n=24; p=0,6; q=0,4. Найдем наивероятнейшее число годных к продаже образцов товаров из двойного неравенства . Подставляя данные задачи, получим
, или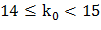 
.
Так как 
– целое число, то и наивероятнейших чисел два: и 
.
№148 Найти наивероятнейшее число правильно набитых перфораторщицей, среди 19 перфокарт, если вероятность того, что перфокарта набита неверно, равна 0,1.
Решение.
По условию, n=19; p=0,9; q=0,1. Найдем наивероятнейшее число правильно набитых перфокарт из двойного неравенства . Подставляя данные задачи, получим
или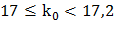 
.
Так как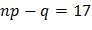 
– целое число, то наивероятнейшее число 
.
№149 Два равносильных противника играют в шахматы. Найти наивероятнейшее число выигрышей для любого шахматиста, если будет сыграно 2N результативных (без ничьих) партий.
Решение:
Известно, что если произведение числа испытаний n на вероятность р появления события в одном испытании есть целое число, то наивероятнейшее число
.
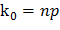В рассматриваемой задаче число испытаний n равно числу сыгранных партий 2N; вероятность появления события равна вероятности выигрыша в одной партии, т. е. р = 1/2 (так как по условию противники равносильны).
Поскольку произведение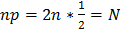 
— целое число, то искомое наивероятнейшее число выигранных партий равно N.
№150 Два стрелка стреляют по мишени. Вероятность промаха при одном выстреле для первого стрелка равна 0,2, а для второго – 0,4. Найти наивероятнейшее число залпов, при которых не будет ни одного попадания в мишень, если стрелки произведут 25 залпов.
Решение:
Промахи стрелков есть независимые события, поэтому применима теорема умножения вероятностей независимых событий. Вероятность того, что оба стрелка при одном залпе промахнуться, p=0,2*0,4=0,08.
Поскольку произведение 
-целое число, то наивероятнейшее число залпов, при которых не буде ни одного попадания,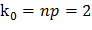 
Ответ: 2.
№151 Два стрелка одновременно стреляют по мишени. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,8, а для второго-0,6. Найти наивероятнейшее число залпов, при которых оба стрелка попадут в мишень, если будет произведено 15 залпов.
Решение:
Попадания стрелков есть независимые события, поэтому применима теорема умножения вероятностей независимых событий. Вероятность того, что оба стрелка при одном залпе попадут р=0,8*0,6=0,48
nр=15*0,48=7,2
6,68<=k0<7,68
Наивероятнейшее число залпов, при которых оба стрелка попадут в мишень равно 7.
№152 Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
Решение:
По условию k0=2;p=0,4;q=0,6. Воспользуемся двойным неравенством:
np-q≤k0<np+p.
Подставляя данные задачи, получим систему неравенств для определения неизвестного числа:
0,4n-0,6≤25; 0,4n+0,4>25.
Из первого неравенства системы найдем: n≤25,60,4=64;
Из второго неравенства системы имеем: n>24,60,4=61,5;
Итак, искомое число испытаний должно удовлетворять двойному неравенству:62≤n≤64.
№153 По условию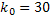 
; 
; 
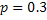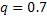. Воспользуемся двойным неравенством
Подставляя данные задачи, получим систему неравенств для определения неизвестного числа:
, 
.
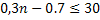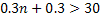Из первого неравенства системы найдем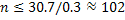 
.
Из второго неравенства системы найдем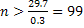 
.
Итак, искомое число испытаний должно удовлетворить двойному неравенству 
.
№154.....
№155 Чему равна вероятность p наступления события в каждом из 49 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 30?
Решение.
По условию, n=49, k0=30. Воспользуемся двойным неравенством 
. Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности p:
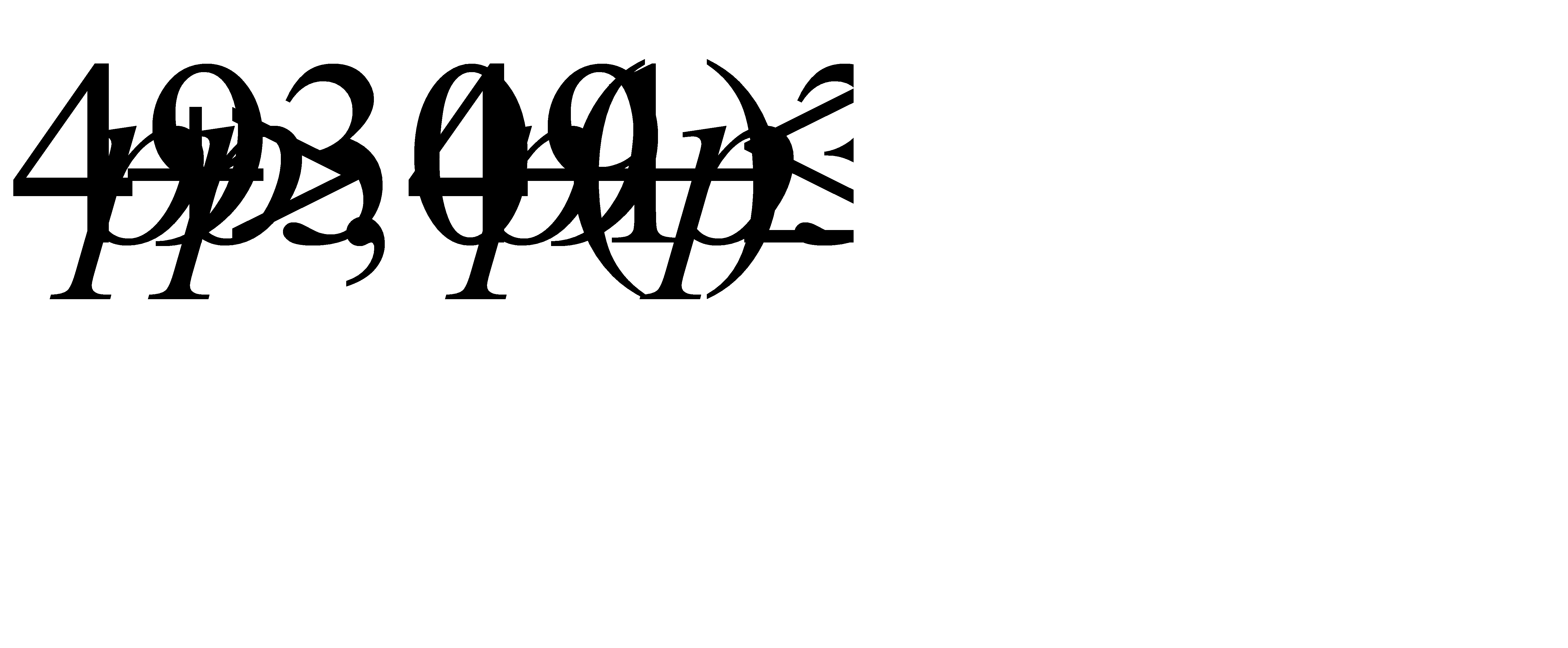
Из первого неравенства системы найдем p>0,6. Из второго неравенства системы найдем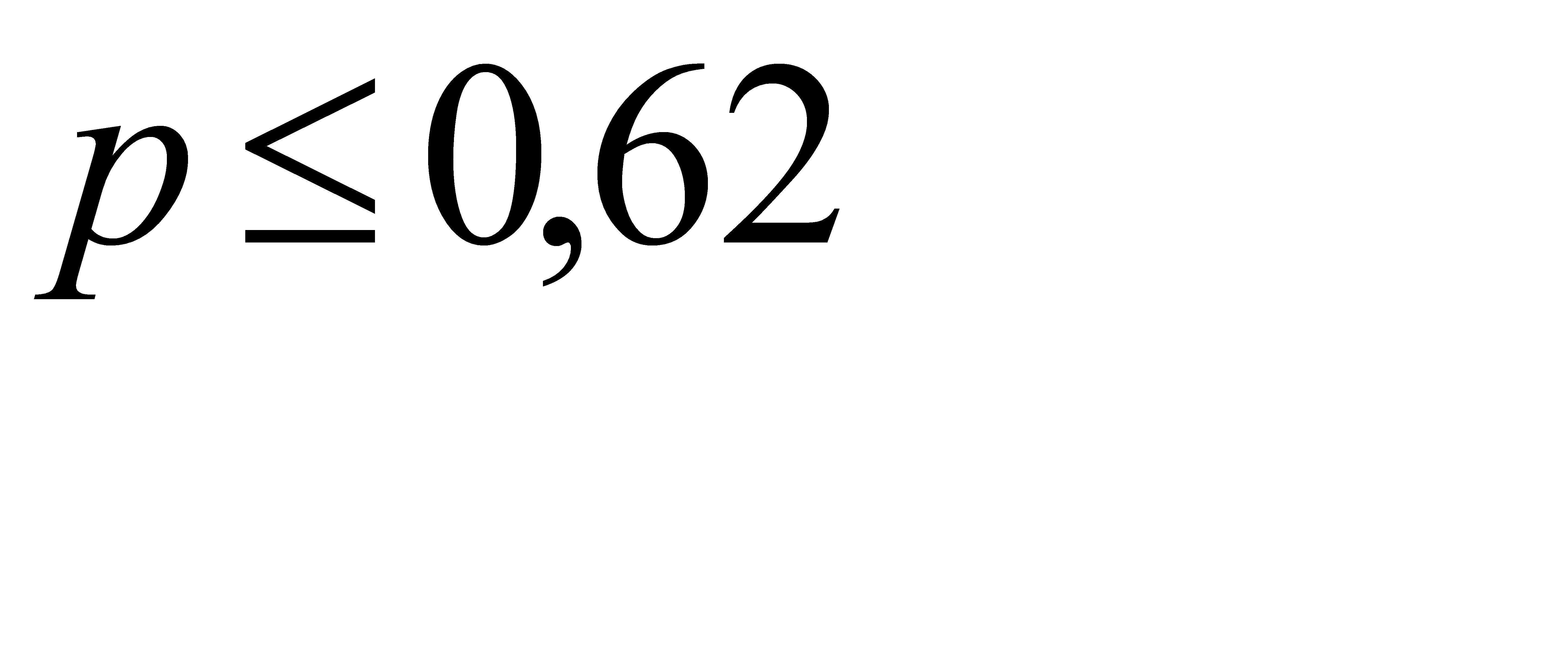 
.
№156 Чему равна вероятность р наступления события в каждом из 39 независимых испытаний, если наивероятнейшее число наступлений события в этих испытаниях равно 25?
Решение
По условию n = 39,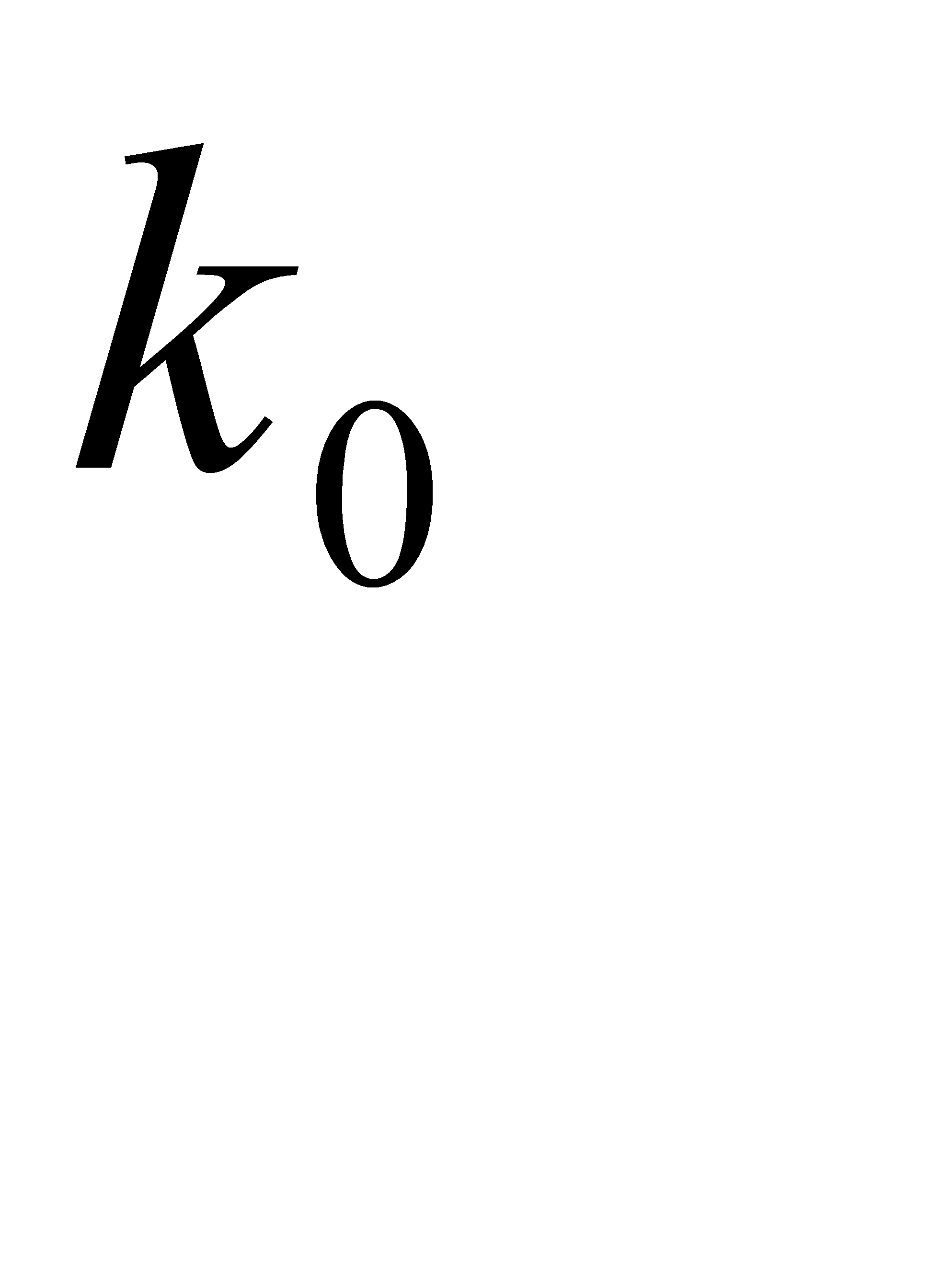 
=25. Воспользуемся двойным неравенством 
. Подставляя данные задачи, получим систему неравенств для определения неизвестной вероятности р:
, 
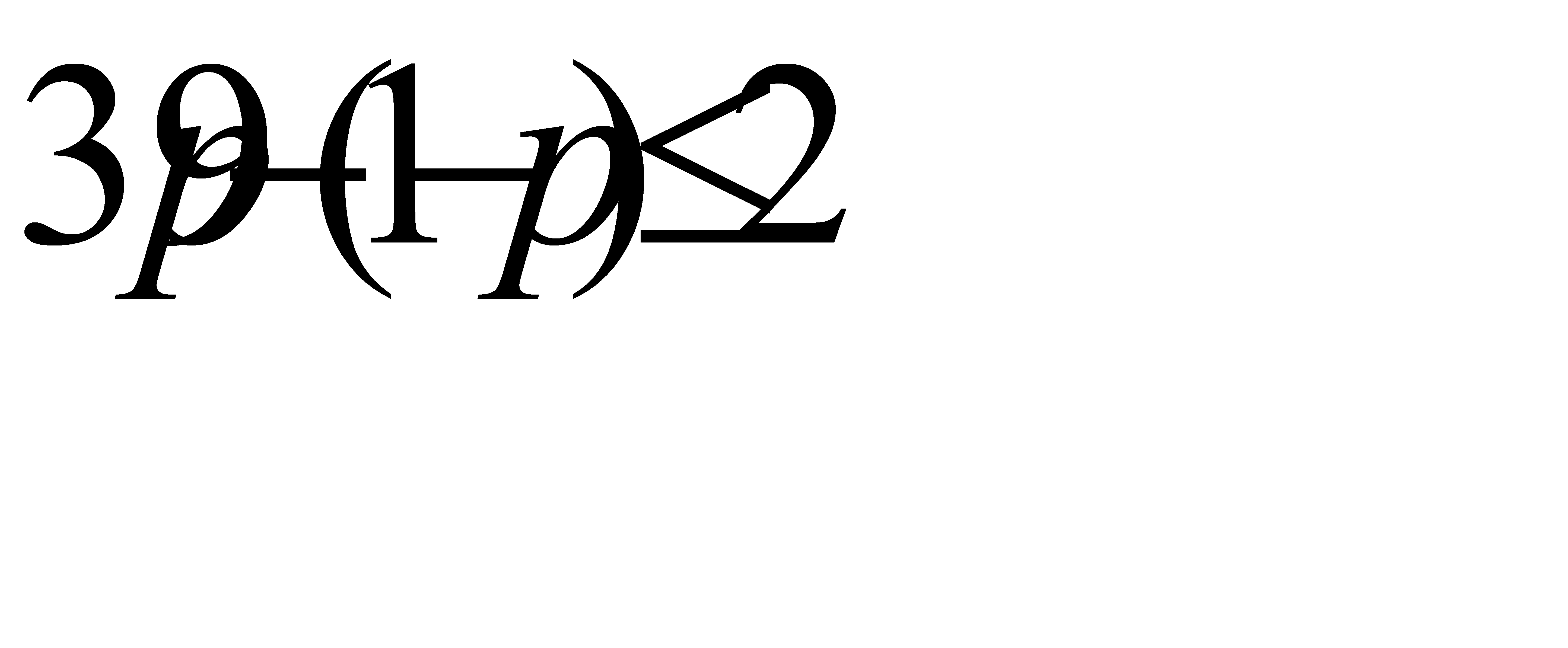
Из первого неравенства системы найдём p>0,625, из второго неравенства системы найдём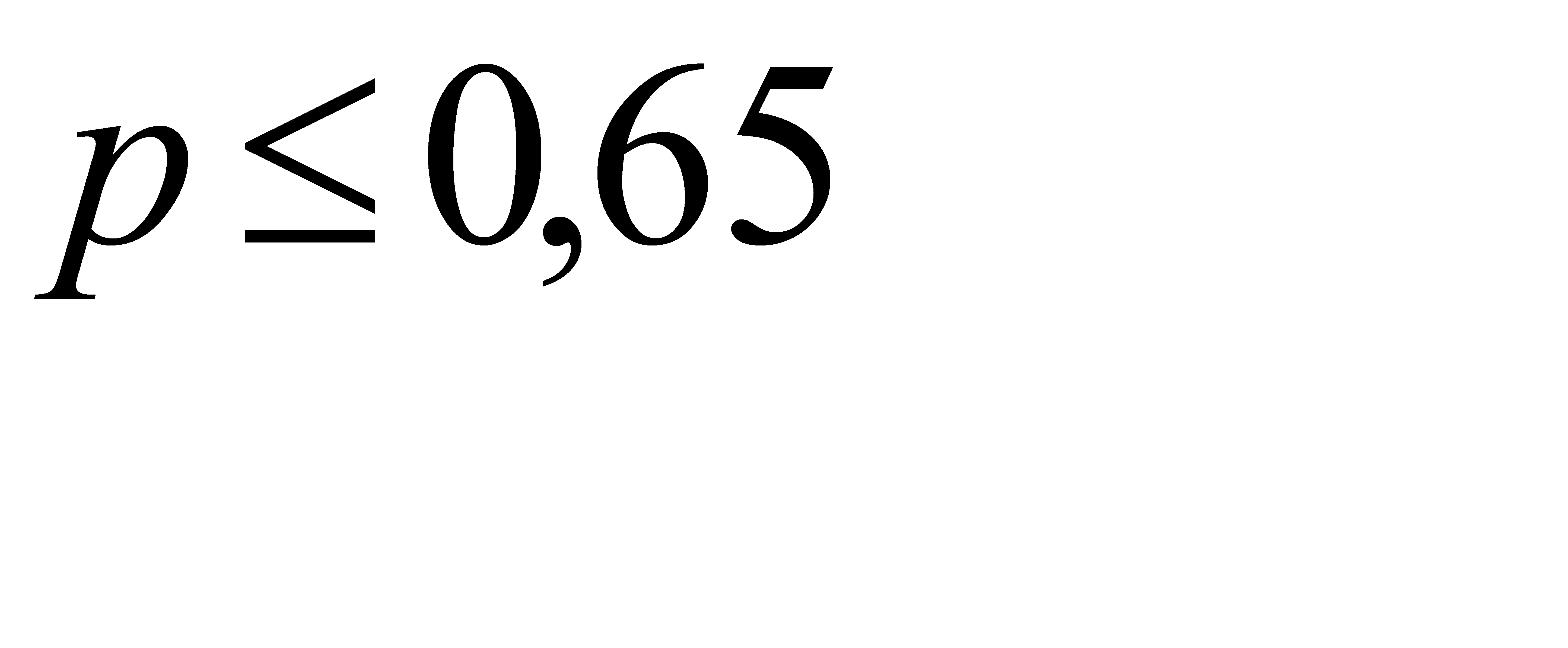 
.
Итак, искомая вероятность должна удовлетворять двойному неравенству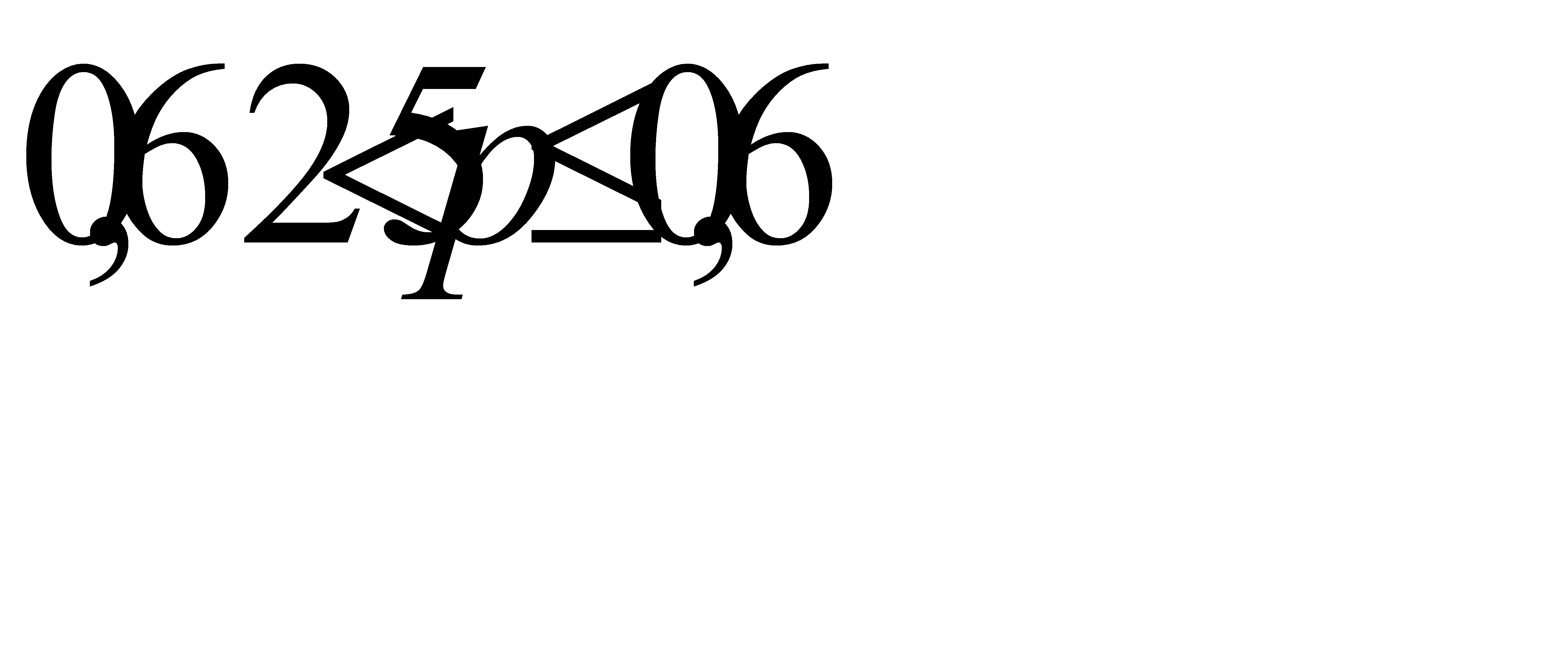 
.
Ответ: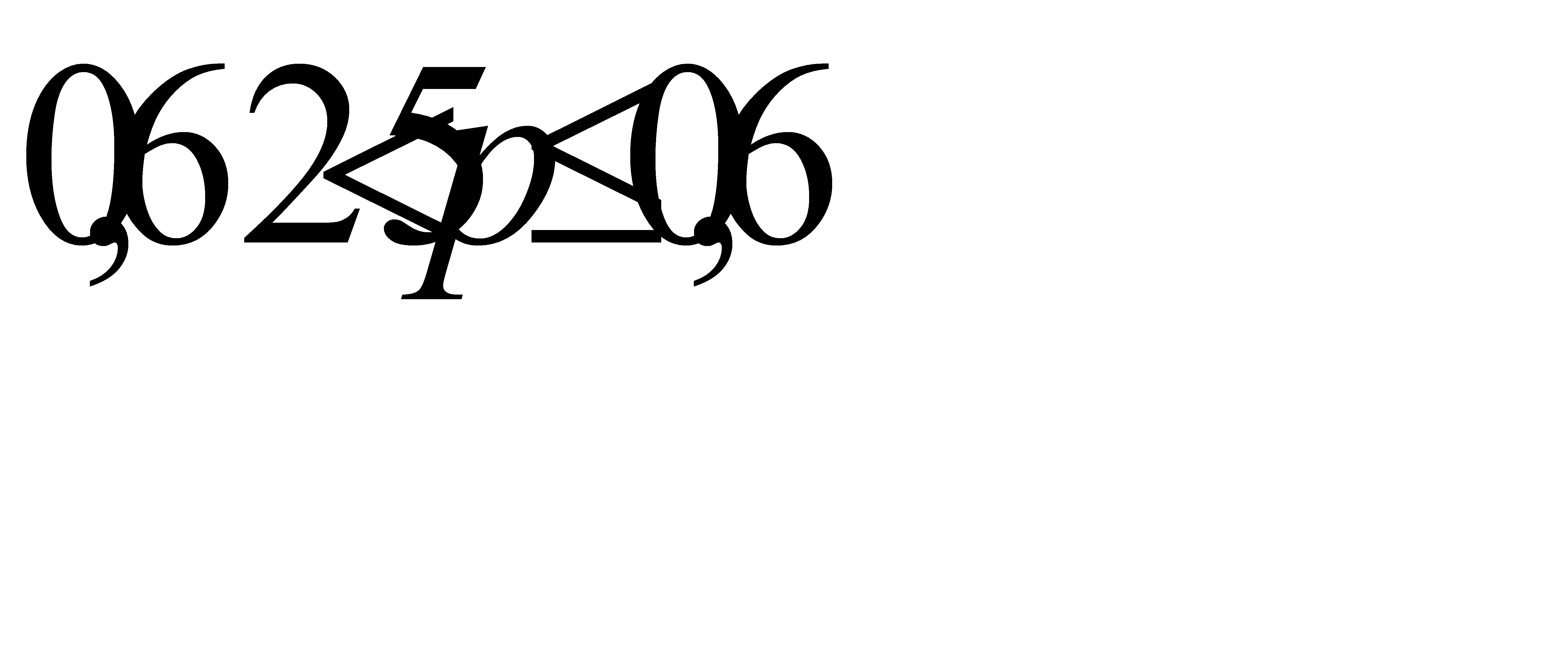
№157 Батарея произвела шесть выстрелов по объекту. Вероятность попадания в объект при одном выстреле равна 0,3. Найти: а) наивероятнейшее число попаданий;
б) вероятность наивероятнеишего числа попаданий; в)вероятность того, что объект будет разрушен, если для этого достаточно хотя бы двух попаданий.
Решение:
По условию, n=6; р=0,3; q=0,7.
а) Найдем наивероятнейшее число попаданий по формуле
np—q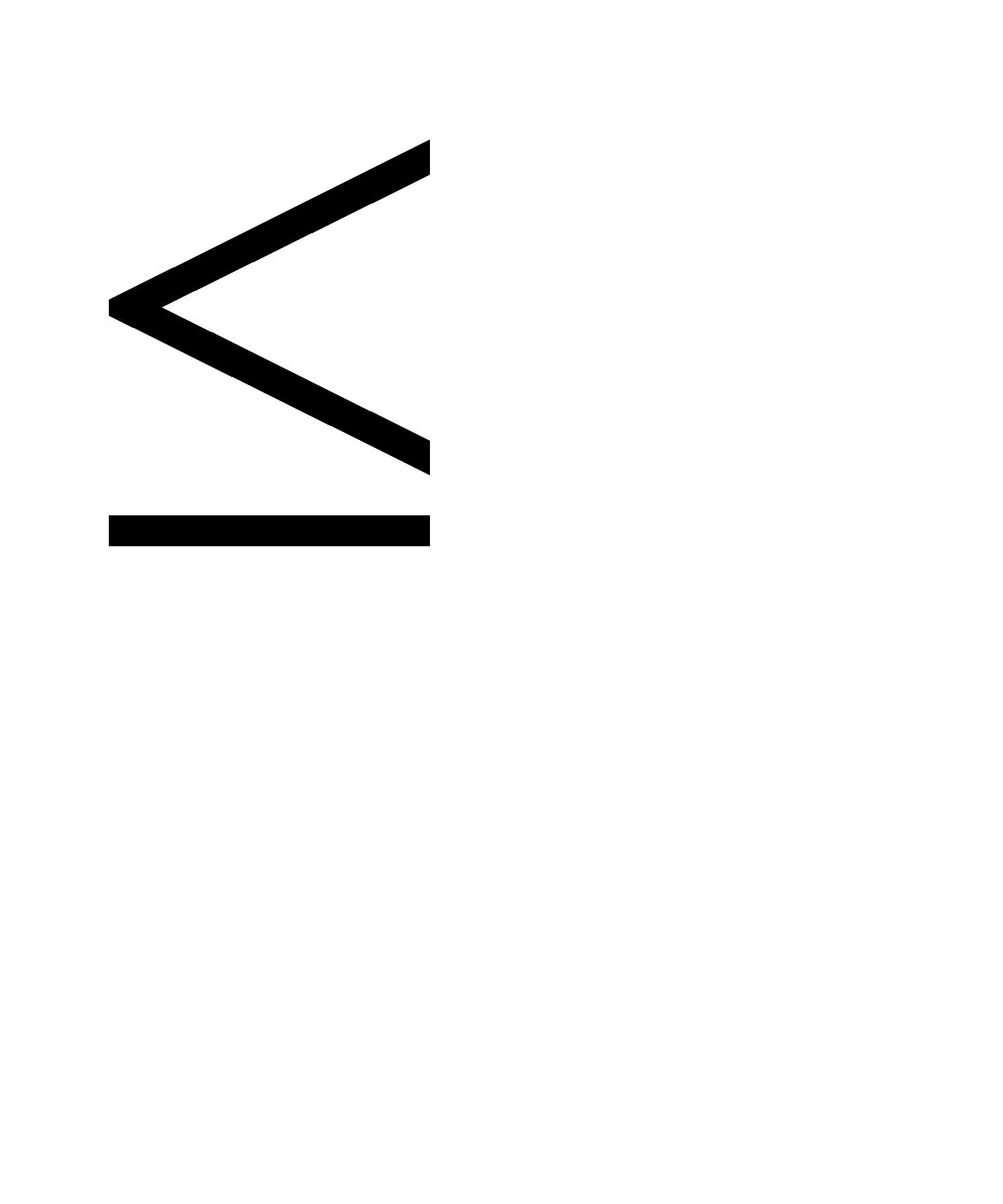 
k 
< nр + р.
Подставив данные задачи, получим
6*0,3—0,7 k < 6*0,3 + 0,3 или 1,1<k <2,1. Отсюда k =2.
б) Найдем вероятность наивероятнеишего числа попаданий по формуле Бернулли
в) Найдем вероятность того, что объект будет разрушен. По условию, для этого достаточно, чтобы было или 2, или 3, или 4, или 5, или 6 попаданий. Эти события несовместны, поэтому вероятность разрушения объекта равна сумме вероятностей этих событий:
Однако проще сначала найти вероятность Q противоположного события (ни одного попадания или одно попадание):
Искомая вероятность того, что объект будет разрушен,
P=l—Q=l—0,42=0,58.
Ответ:а)2, б)0,324, в)0,58
№158 Прибор состоит из пяти независимо работающих элементов. Вероятность отказа элемента в момент включения прибора равна 0,2. Найти а) наивероятнейшее число отказавших элементов; б) вероятность наивероятнейшего числа отказавших элементов; в) вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы четыре элемента.
Решение:
По условию, n= 5; p= 0,2; q= 0,8;
а) Найдем наивероятнейшее число отказов по формуле 
. Подставив данные задачи, получим: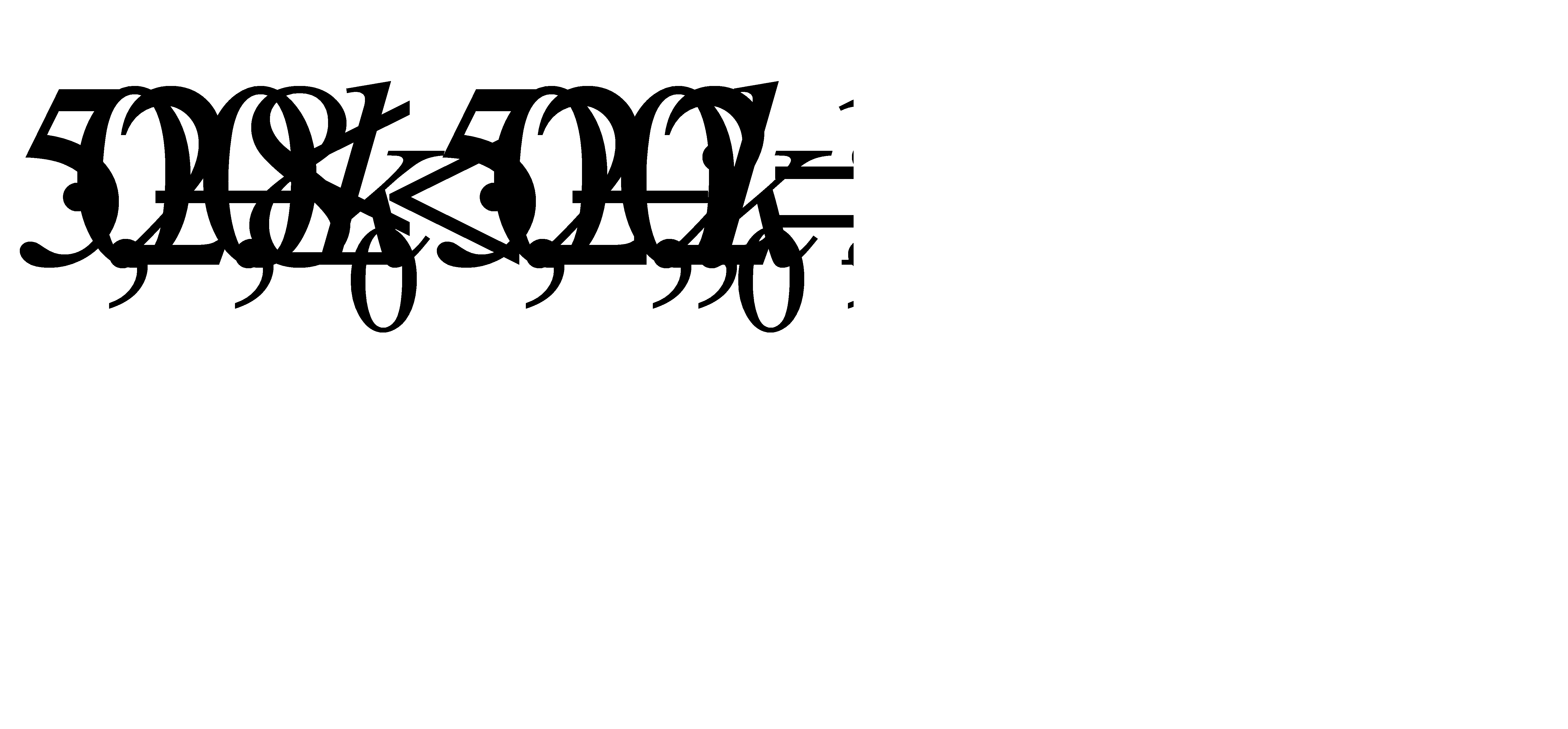 
.
б) Найдем вероятность наивероятнейшего числа отказов по формуле Бернулли
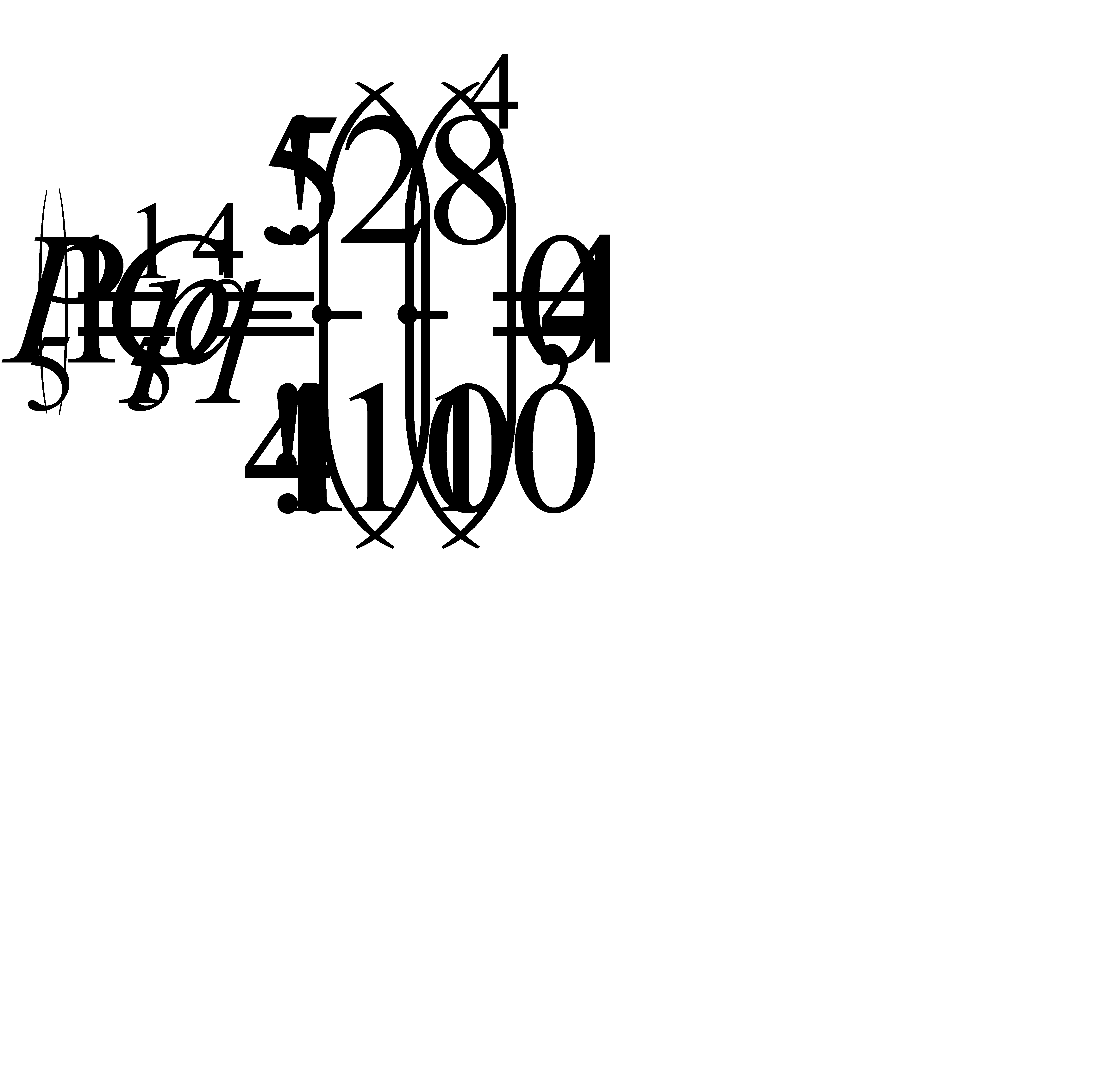
в) Найдем вероятность отказа прибора. Для того чтобы прибор был разрушен по условию задачи достаточно чтобы отказали 4 или 5 элементов.
№159 Устройство состоит из трех независимо работающих элементов. Вероятности безотказной работы элементов (за время t) соответственно равны: 0,7; 0,8 и 0,9. Найти вероятности того, что за время t будут работать безотказно:
а) все элементы; б) два элемента; в) один элемент; г) ни один из элементов.
Решение.
Вероятности безотказной работы элементов соответственно равны:
р1 = 0,7, р2 = 0,8, р3 = 0,9, поэтому вероятности того, что элементы откажут, q1 = 0,3; q2 = 0,2; q3=0,1.
Составим производящую функцию:
φ3(z) = (p1∙z + q1) (p2∙z + q2) (p3∙z + q3) = (0,7z + 0,3)(0,8z + 0,2)(0,9z + 0,1) = 0,504z3 + 0,398z2 + 0,092z + 0,006.
а) Вероятность того, что три элемента будут работать безотказно, равна коэффициенту при z3: Р3(3) = 0,504.
б) Вероятность того, что два элемента будут работать безотказно, равна коэффициенту при z2: Р3(2) = 0,398.
в) Вероятность того, что один элемент будет работать безотказно, равна коэффициенту при z1: Р3(1) = 0,092.
г) Вероятность того, что ни один из элементов не будет работать безотказно, равна свободному члену: Р3(0) = 0,006.
Контроль: 0,504 + 0,398 + 0,092 + 0,006 = 1.
Олейников Илья
№161 Из трех орудий произведен залп по цели. Вероятность попадания в цель для первого орудия равна 0,8, для второго — 0,85, для третьего — 0,9. Найти вероятности следующих событий: а) три попадания в цель; б) два попадания в цель; в) одно попадание; г) ни одного попадания в цель; д) хотя бы одно попадание в цель
Решение.
Вероятности попаданий соответственно равны ;
;
, поэтому вероятности того, орудия промахнутся,
;
.
Составим производящую функцию:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту
при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту
при :
.
в) Вероятность того, только одно орудие попадет в цель равна коэффициенту
при :
.
г) Вероятность того, что ни одно орудие не попадет в цель равна свободному
члену: .
д) Вероятность того, что хотя бы одно орудие попадет в цель равна: .
№162 Четыре элемента вычислительного устройства работают независимо. Вероятность отказа первого элемента за время t равна 0,2, второго — 0,25, третьего — 0,3, четвертого — 0,4. Найти вероятность того, что за время t откажут: а) 4 элемента; б) 3 элемента; б) 2 элемента; г) 1 элемент; д) ни один элемент; е) не более двух элементов.
Решение.
Вероятности того, что элементы откажут равны
, поэтому вероятности безотказной работы,
.
