Составим производящую функцию:
а) Вероятность того, что все четыре элемента откажут равна коэффициенту
при :
.
б) Вероятность того, что три элемента откажут равна коэффициенту
при :
.
в) Вероятность того, два элемента откажут равна коэффициенту
при :
.
г) Вероятность того, только один элемент откажет равна коэффициенту
при :
г) Вероятность того, что ни один элемент не откажет равна свободному члену: .
д) Вероятность того, что не более двух элементов откажет равна: .
№163 Две батареи по 3 орудия каждая производят залп по цели. Цель будет поражена, если каждая из батарей даст не менее двух попаданий. Вероятности по падания в цель орудиями первой батареи равны 0,4; 0,5; 0,6, второй—0,5; 0,6; 0,7. Найти вероятность поражения цели при одном залпе из двух батарей.
Решение.
Из условия задачи следует, что необходимо попадание хотя бы четырех орудий. То есть либо трех из одной + одно из другой..
Составим производящую функцию для первой батареи:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту
при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту
при :
.
Вероятность того, что в цель попадет как минимум 2 снаряда равна:
Составим производящую функцию для второй батареи:
а) Вероятность того, что все три орудия попадут в цель равна коэффициенту
при :
.
б) Вероятность того, что два орудия попадут в цель равна коэффициенту
при :
.
Вероятность того, что в цель попадет как минимум 2 снаряда равна:
Таким образом вероятность уничтожения цели равна
№164 Дискретная случайная величина Х задана законом распределения:
Х 1 3 6 8
Р 0,2 0,1 0,4 0,3
Построить многоугольник распределения.
Решение:
Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат- соответствующие вероятность pi. Построим точки
Полученный многоугольник и есть искомый многоугольник распределения.
№165 Дискретная случайная величина X задана законом распределения:
а) X 2 4 5 6 б) X 10 15 20
р 0,3 0,1 0,2 0,4 р 0,1 0,7 0,2
Построить многоугольник распределения.
Решение.
Построим прямоугольную систему координат, при-
причем по оси абсцисс будем откладывать возможные значения х; а по
оси ординат — соответствующие вероятности р.
Построим точки:
а)А(2; 0,3), В(4;0,l), С(5;0,2) и D(6; 0,4). Соединив эти точки
отрезками прямых, получим искомый многоугольник распределения.
б)А(10; 0,1), В(15;0,7), С(20;0,2). Соединив эти точки
отрезками прямых, получим искомый многоугольник распределения.
№166 Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение
Дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: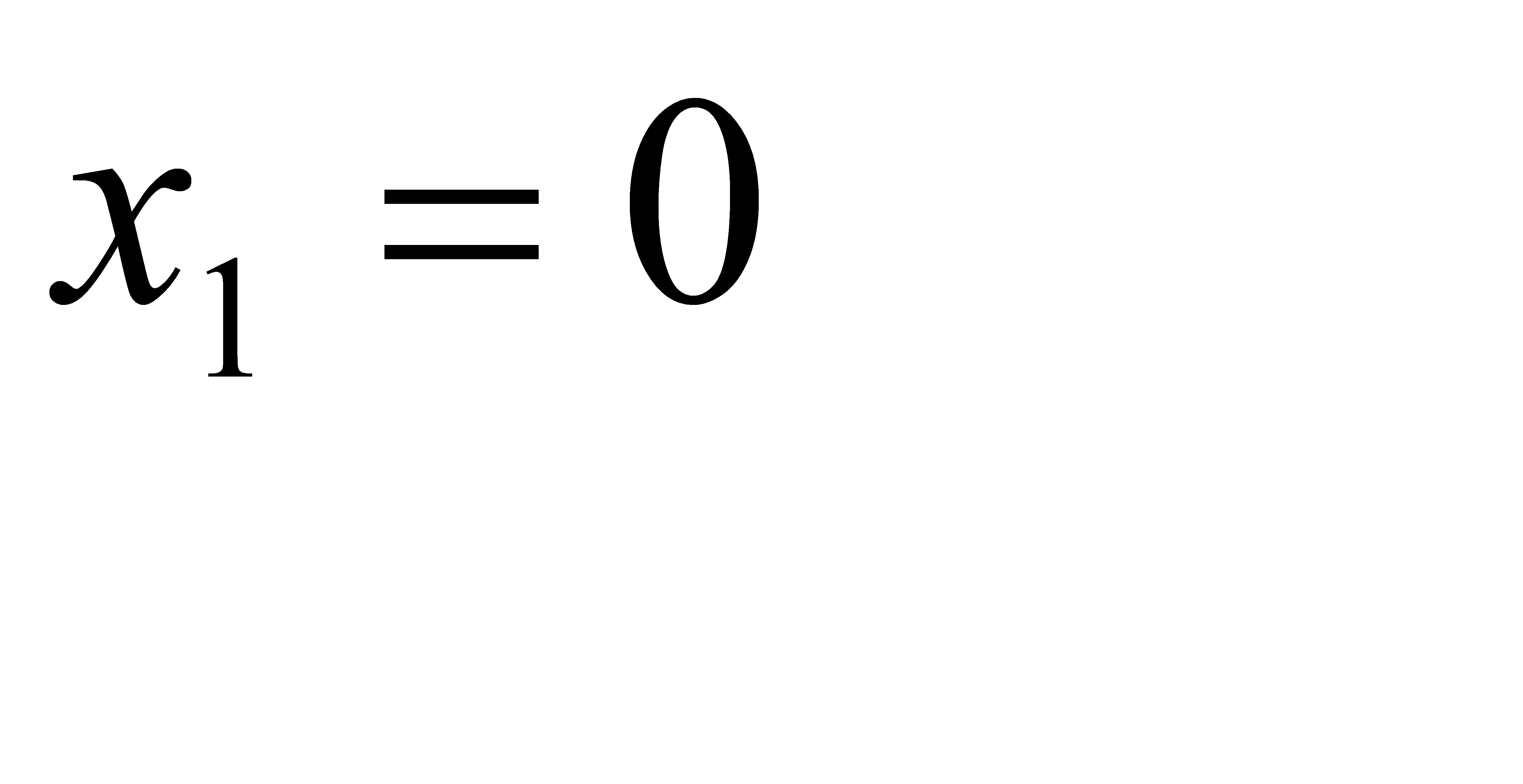 
(ни один из элементов устройства не отказал), 
(отказал один элемент), 
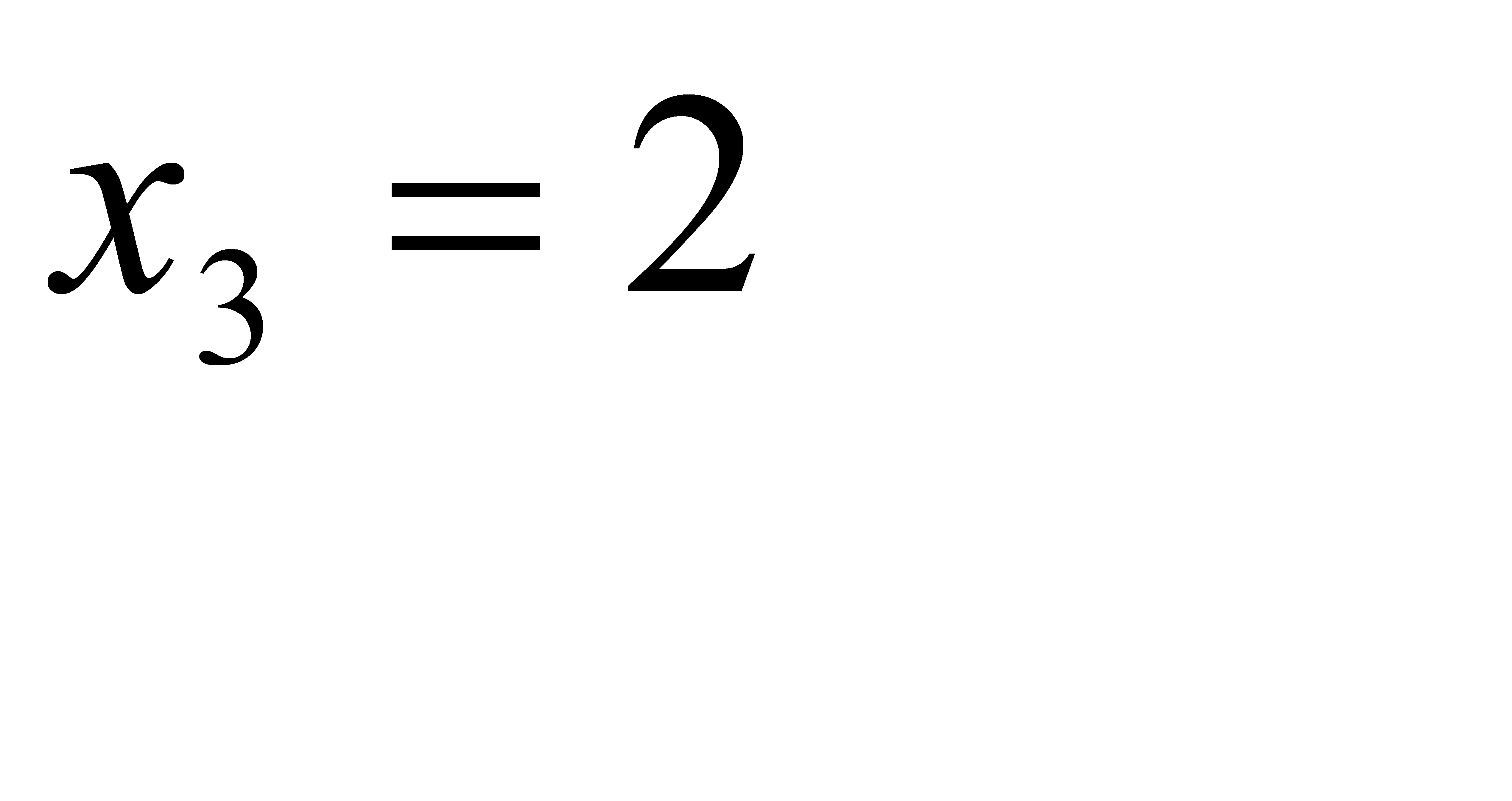(отказали 2 элемента) и 
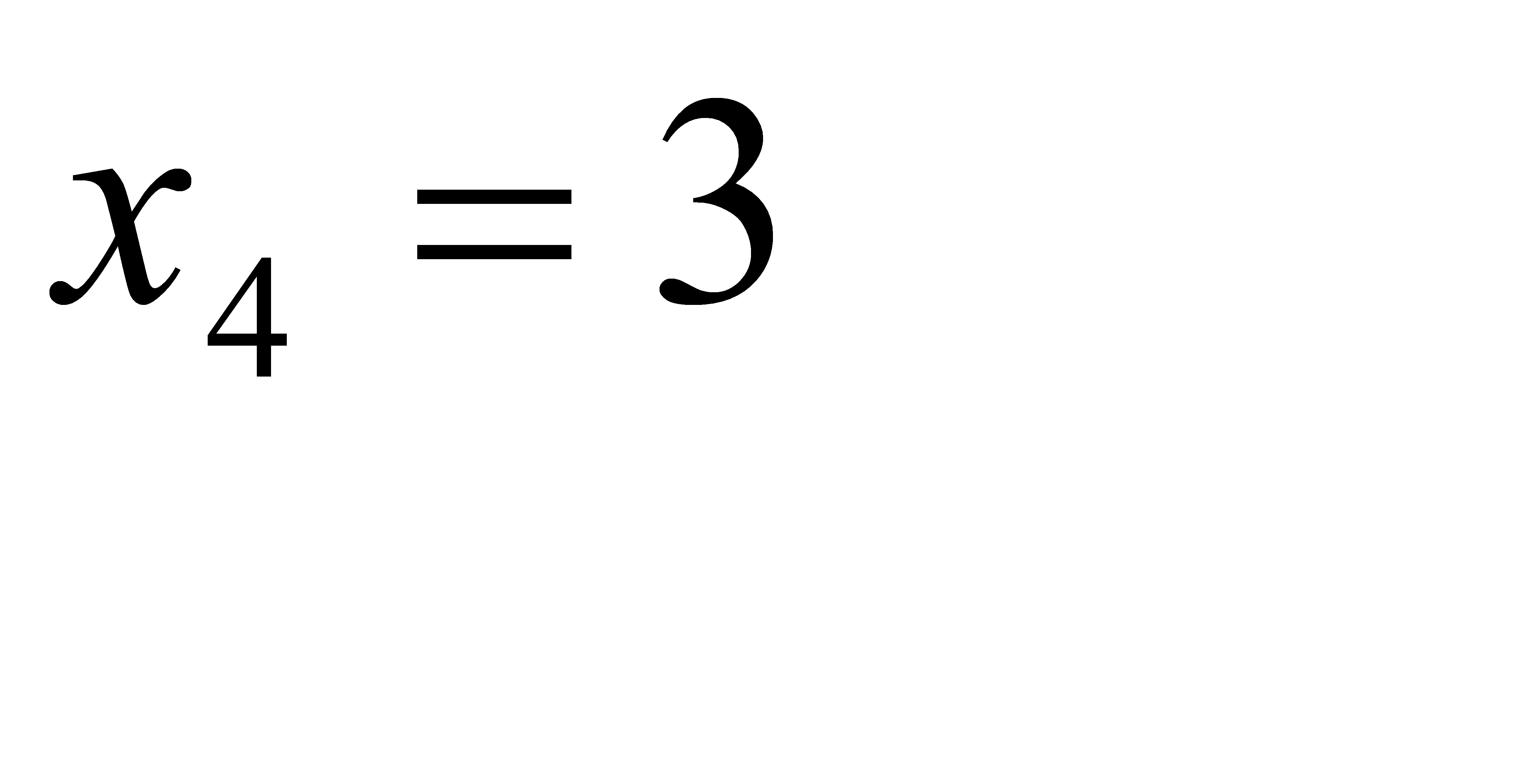(отказали 3 элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что по условию n = 3, p = 0,1 (следовательно q = 0,9), получим:
; 
;
; 
.
Проверим: 
.
Напишем искомый биномиальный закон распределения Х:
X 0 1 2 3
p 0,729 0,243 0,027 0,001
№167 В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины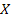 
—числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
Решение
Дискретная случайная величина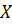 
(число нестандартных деталей среди 4 отобранных) имеет следующие возможные значения: 
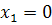(отобрали только стандартные детали), 
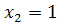(отобрали одну нестандартную и три стандартных), 
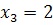(отобрали две нестандартных и две стандартных), 
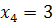(отобрали три нестандартных и одну стандартную), 
(отобрали только нестандартные). Вероятность отобрать из партии нестандартную деталь 
. По условию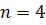 
. Найдём 
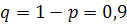. Получим:
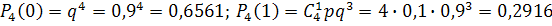
Напишем искомый биномиальный закон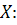 
| Возможные значения | |||||
| Вероятности | 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0.0001 |
Построим многоугольник распределения дискретной случайной величины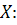
№168 Написать биноминальный закон распределения дискретной случайной величины X –числа появлений «герба» при двух бросаниях монеты.
Решение:
Дискретная случайная величина 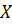(число появлений «герба» при двух бросаниях монеты) имеет следующие возможные значения: («герб» ни разу не выпал), («герб» выпал только при одном броске), («герб» выпадал при каждом броске).
Очевидно что искомый биномиальный закон будет выглядеть следующим образом:
| Возможные значения | |||
| Вероятности | 1/4 | 1/2 | 1/4 |
№169 Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X – числа выпадений четного числа очков на двух игральных костях.
Решение
Всего вариантов выпадений: 6*6=36.
Четных 3 грани на каждом кубике => 3*3=9 – четное число очков на каждой игральной кости.
p=9/36=1/4 – вероятность выпадения четного числа очков на каждой игральной кости.
q=1-p=3/4
Pn(k)=Cnk*pk*qn-k
Pn(0)=9/16 Pn(1)=6/16 Pn(0)=1/16
X 0 1 2
P 9/16 6/16 1/16
№170 В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Обставить закон распределения числа стандартных деталей среди отобранных.
Решение
Случайная величина X—число стандартных деталей среди отобранных деталей—имеет следующие возможные значения: X1=0; X2=1; X3=2; Найдем вероятности возможных значений X по Формуле: PX=k= Cnk*CN-nm-kCNm.
(N—число деталей в партии, n— число стандартных деталей в партии, m— число отобранных деталей, k— число стандартных деталей среди отобранных), находим:
PX=0=C80*C22C102=145;
PX=1=C81*C21C102=1645;
PX=2=C82*C20C102=2845;
Составим искомый закон распределения:
| X | |||
| P | 1/45 | 16/45 | 28/45 |
Контроль: 1/45+16/45+28/45=1.
№171 В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины Х-числа стандартных деталей, среди отобранных.
Решение:
Случайная величина Х имеет следующие возможные значения х1=1, х2=2, х3=3.
Найдем вероятности возможных значений Х.
Р(Х=1)=С41 С22 /С63=1/5
Р(Х=2)=С42 С21 /С63=3/5
Р(Х=3)=С43 С20 /С63=1/5
Составим искомый закон распределения:
Х 0 1 2 3
Р 0 1/5 3/5 1/5
№172 После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные вопросы, как только студент обнаруживает незнание данного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 0,9. Требуется: а)составить закон распределения случайной дискретной величины Х – числа дополнительных вопросов, которые задаст преподаватель студенту; б) найти наивероятнейшее число k0 дополнительных вопросов.
Решение:
а) Дискретная случайная величина Х – число заданных вопросов – имеет следующие возможные значения: x1=1, x2=2, x3=3,…, xk=k,… Найдем вероятности этих возможных значений.
Величина Х примет возможное значение x1=1 (экзаменатор задаст только один вопрос), если студент не ответит на первый вопрос. Вероятность этого возможного значения равна 1-0,9=0,1. Таким образом, P(X=1)=0,1.
Величина Х примет возможное значение x2=2 (экзаменатор задаст только два вопроса), если студент ответит на первый вопрос и не ответит на второй. Таким образом, P(X=2)=0,9*0,1=0,09.
Аналогично найдем P(X=3)=0,9*0,9*0,1=0,081, …,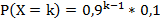 
Выпишем искомый закон распределения:
| X | … | k | … | |||
| p | 0,1 | 0,09 | 0,081 | … |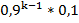 
| … |
б) Наивероятнейшее число k0 заданных вопросов (наивероятнейшее возможное значение Х), т.е. число заданных преподавателем вопросов, которое имеет наибольшую вероятность, как следует из закона распределения, равно 1.
№173 Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины X—числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.
Решение:
а) Дискретная случайная величина Х – число выданных патронов – имеет следующие возможные значения: x1=1, x2=2, x3=3,…, xk=k,… Найдем вероятности этих возможных значений.
Величина Х примет возможное значение x1=1 (выдадут только один патрон), если не попадет при первом выстреле. Вероятность этого возможного значения равна 1-0,8=0,2. Таким образом, P(X=1)=0,2.
Величина Х примет возможное значение x2=2 (выдадут два патрона), если попадет первый раз, но промахнется во второй. Таким образом, P(X=2)=0,8*0,1=0,08.
Аналогично найдем P(X=3)=0,8*0,8*0,2=0,128, …, 
Выпишем искомый закон распределения:
| X | … | k | … | |||
| p | 0,2 | 0,08 | 0,128 | … |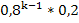 
| … |
б) Наивероятнейшее число k0 выданных патронов (наивероятнейшее возможное значение Х), т.е. число выданных патронов, которое имеет наибольшую вероятность, как следует из закона распределения, равно 1.
Ответ: а) 0,2, 0,08, …, 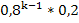б) 1.
№174 Из двух орудий поочередно ведется стрельба по цели до первого попадания одним из орудий. Вероятность попадания в цель первым орудием равна 0,3, вторым — 0,7.
Начинает стрельбу первое орудие. Составить законы распределения дискретных случайных величин X и Y—числа израсходованных снарядов соответственно первым и вторым орудием.
Решение.
Пусть события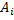 
и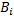 
— попадание в цель соответственно первым и вторым орудием при i-м выстреле; 
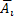и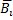 
- промахи.
Найдем закон распределения случайной величины X—числа израсходованных первым орудием снарядов. Первое орудие израсходует один снаряд (Х=1), если оно попадет в цель при первом
выстреле, или оно промахнется, а второе орудие при первом выстреле попадет в цель:
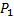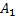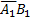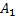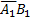=P(X=1)=P(
+ 
)=P(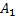)+P()= P(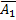)+ P(
)* P(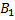
)=0,3+0,7*0,7=0,79.
Первое орудие израсходует два снаряда, если оба орудия при первом выстреле промахнутся, а при втором выстреле первое орудие попадет в цель, или если оно промахнется, а второе орудие при втором выстреле попадет в цель:
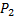=P(X = 2)=Р(
+ 
)=
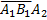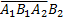= 0,7*0,3*0,3 + 0,7*0,3*0,7*0,7 = 0,21 (0,3 + 0,49) = 0,79*0,21.
Аналогично получим
Р(Х=k)=0,79*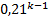 
.
Искомый закон распределения дискретной случайной величины X— числа снарядов, израсходованных первым орудием:
| X | … | k | … | |||
| p | 0,79 | 0,79*0,21 | 0,79*0,212 | … | 0,79*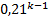
| … |
Контроль: 
= 0,79/(1-0,21) =0,79/0,79=1.
Найдем закон распределения дискретной случайной величины Y—числа снарядов, израсходованных вторым орудием. Если первое орудие при первом выстреле попадет в цель, то
стрельба из второго орудия не будет произведена:
p1=P(Y=0) = P (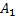) =0,3.
Второе орудие израсходует лишь один снаряд, если при первом выстреле оно попадет в цель, или если оно промахнется, а первое орудие попадет в цель при втором выстреле:
p2 = P(Y=l) = P(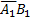 + 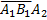) = 0,7*0,7 + 0,7*0,3*0,3 = 0,553.
Вероятность того, что второе орудие израсходует два снаряда,
Рз=Р(Y=2) = Р(
+ 
).
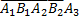Выполнив выкладки, найдем р3 = 0,553*0,21.
Аналогично получим
P(Y=k)=0,553* .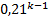
Искомый закон распределения дискретной случайной величины
Y — числа снарядов, израсходованных вторым орудием:
| Y | … | k | … | |||
| p | 0,3 | 0,553 | 0,553*0,21 | … | 0,553*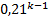
| … |
Контроль: = 0,3+ (0,553/1 —0,21)=0,3+(0,553/0,79) =
= 0,3+0,7=1.
№175 Два бомбардировщика поочередно сбрасывают бомбы на цель до первого попадания. Вероятность попадания в цель первым бомбардировщиком равна 0,7, вторым — 0,8. Вначале сбрасывает бомбы первый бомбардировщик. Составить первые четыре члена закона распределения дискретной случайной величины X—числа сброшенных бомб обоими бомбардировщиками (т. е. ограничиться возможными значениями X, равными 1, 2, 3 и 4).
Решение:
Пусть события Ai и Вi — попадание в цель соответственно первой и второй бомбой при i-ом сбрасывании Ai и Bi— промахи.
Найдем закон распределения случайной величины X—числа израсходованных первым и вторым бомбардировщиком бомб.
Бомбардировщики израсходуют одну бомбу (X=1), если первый бомбардировщик попадет в цель: p1=PX=1=PA1=0,7. Бомбардировщики израсходуют 2 снаряда (X=2), если первый промахнется, а второй попадет в цель: p2=PX=2=PA1B2=0,3*0,8=0,24. Если было израсходовано 3 бомбы (X=3), то только в том случае, если при первом выбросе бомб промазали оба бомбардировщика, а при втором попал первый: p3=PX=3=PA1B1A2=0,3*0,2*0,7=0,042. Четыре бомбы (X=4) понадобятся 2 бомбардировщикам, если попадет в цель лишь второй бомбардировщик при втором выбросе: p4=PX=4=PA1B1A2B2=0,3*0,2*0,3*0,8=0,0144.
Искомый закон распределения дискретной случайной величины X — числа снарядов, израсходованных двумя бомбардировщиками:
| X | ||||
| P | 0,7 | 0,24 | 0,042 | 0,0144 |
№176 Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение.
По условию n=100 000; p=0.0001; k=5. События, состоявшие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность p мала, поэтому воспользуемся распределением Пуассона:
Pn(k)=λke-λ/k
Найдем λ:
λ=np=100 000 * 0,0001=10
Искомая вероятность:
P100 000(5)=105*e-10/5=105*0,000045/120=0,0375
№177 Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента. УКАЗАНИЕ: принять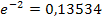 
.
Решение.
По условию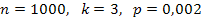 
. Отказ любого элемента в течение времени не зависит от событий в предшествующие моменты времени. Так как число n велико, а вероятность p мала, следует воспользоваться распределением Пуассона (
– это среднее число появлений события в n испытаниях; оно обозначается буквой «лямбда», но MS Word такой буквы не знает):
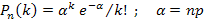
Подставим значения: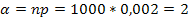 
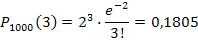
№178 Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна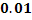 
. Найти вероятность того, что среди 
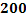деталей окажется ровно 
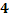бракованных.
Решение:
По условию,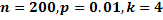 
. События, состоящие в том, что детали окажутся бракованными, независимы, число 
велико, а вероятность 
мала, поэтому воспользуемся распределение Пуассона:
Найдем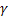 
:
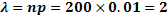
Искомая вероятность:
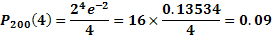
Пискунов Игорь.
№179 Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно.
Решение:
Число n=500 велико, вероятность q= 0,002 мала и рассматриваемые события (повреждения изделий) независимы, поэтому имеет место формула Пуассона.
.
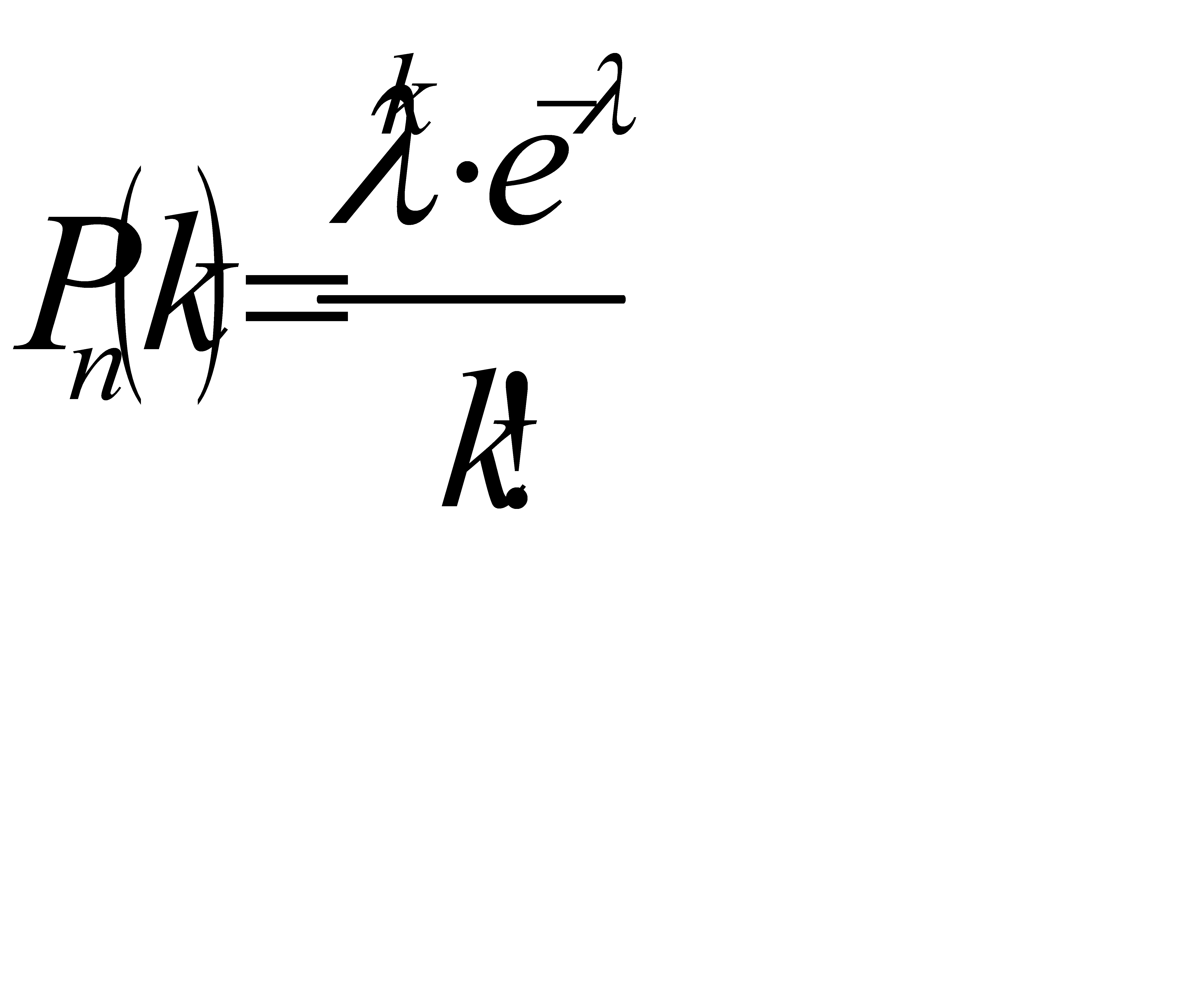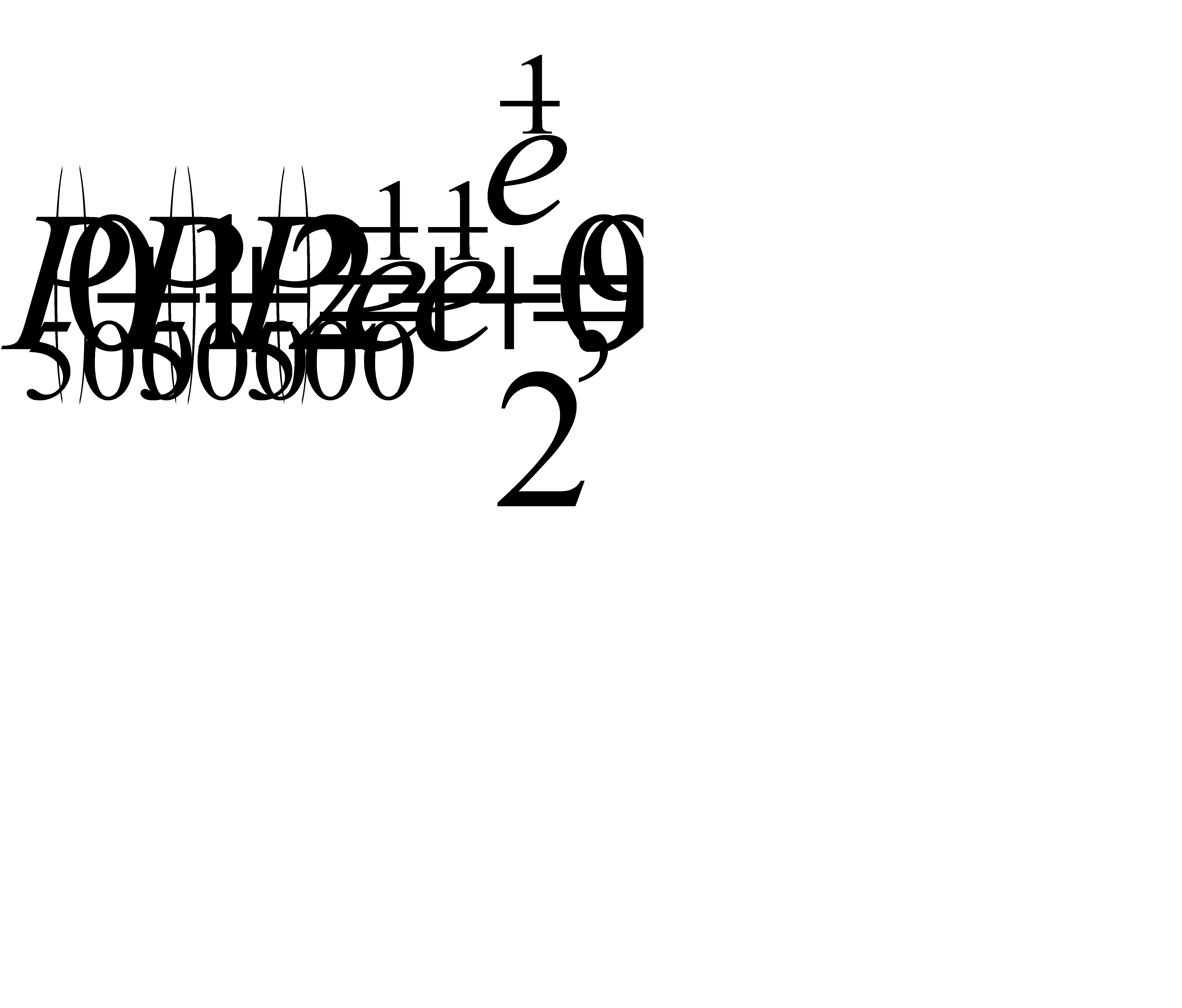
а) Найдем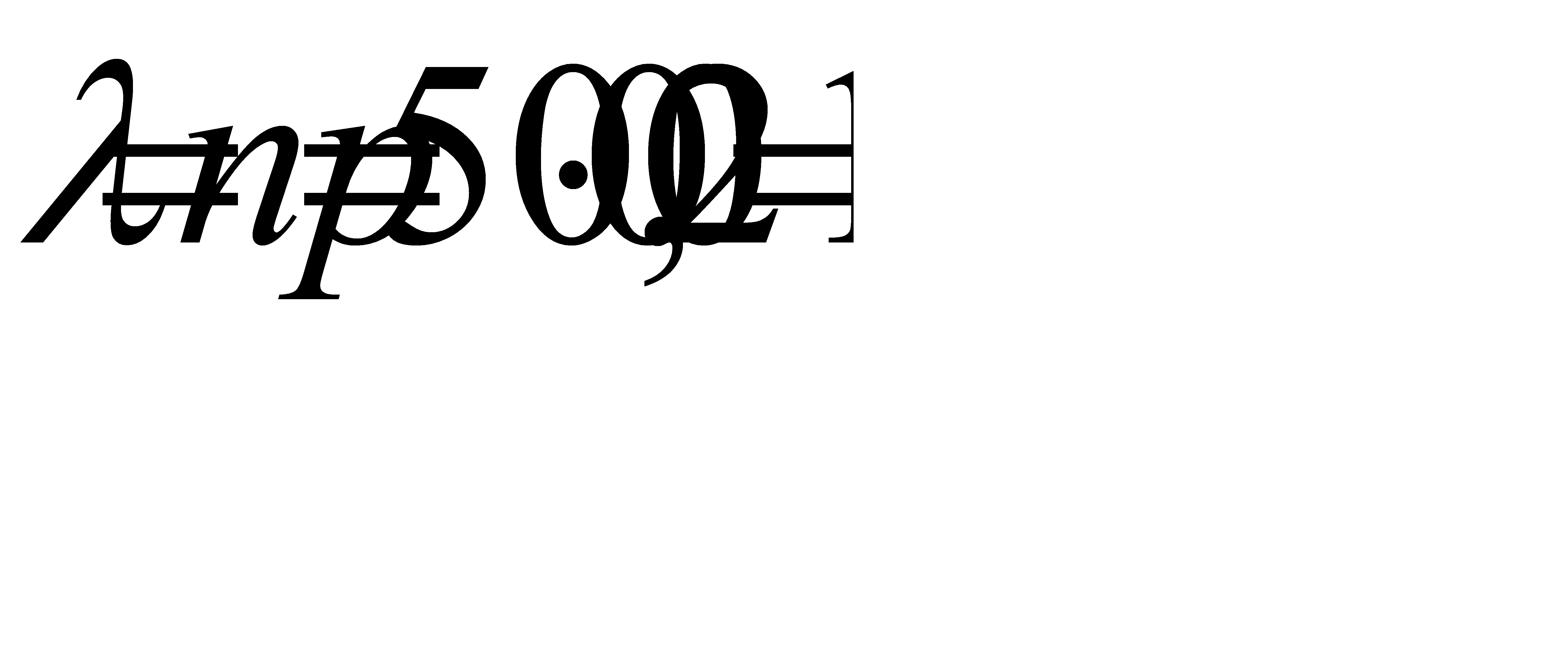 
Найдем вероятность того, что будет повреждено ровно 3 изделия:
б) Найдем вероятность того, что будет повреждено менее трех изделий:
в) Найдем вероятность Р того, что будет повреждено более трех изделий. События «повреждено более трех изделий» и «повреждено не более трех изделий»(обозначим вероятность этого события через Q) – противоположны, поэтому P=1-Q. Отсюда
Используя результаты, полученные выше, имеем
.
г)Найдем вероятность того, что будет повреждено хотя бы одно изделие. События «повреждено хотя бы одно изделие» и «ни одно изделие не повреждено» (обозначим вероятность этого события через Q)- противоположные, следовательно P=1-Q. Отсюда искомая вероятность того, что будет повреждено хотя бы одно изделие, равна
№180 Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятности того,
что магазин получит разбитых бутылок: а) ровно две; б) менее двух;
в) более двух;г) хотя бы одну. Указание. Принять е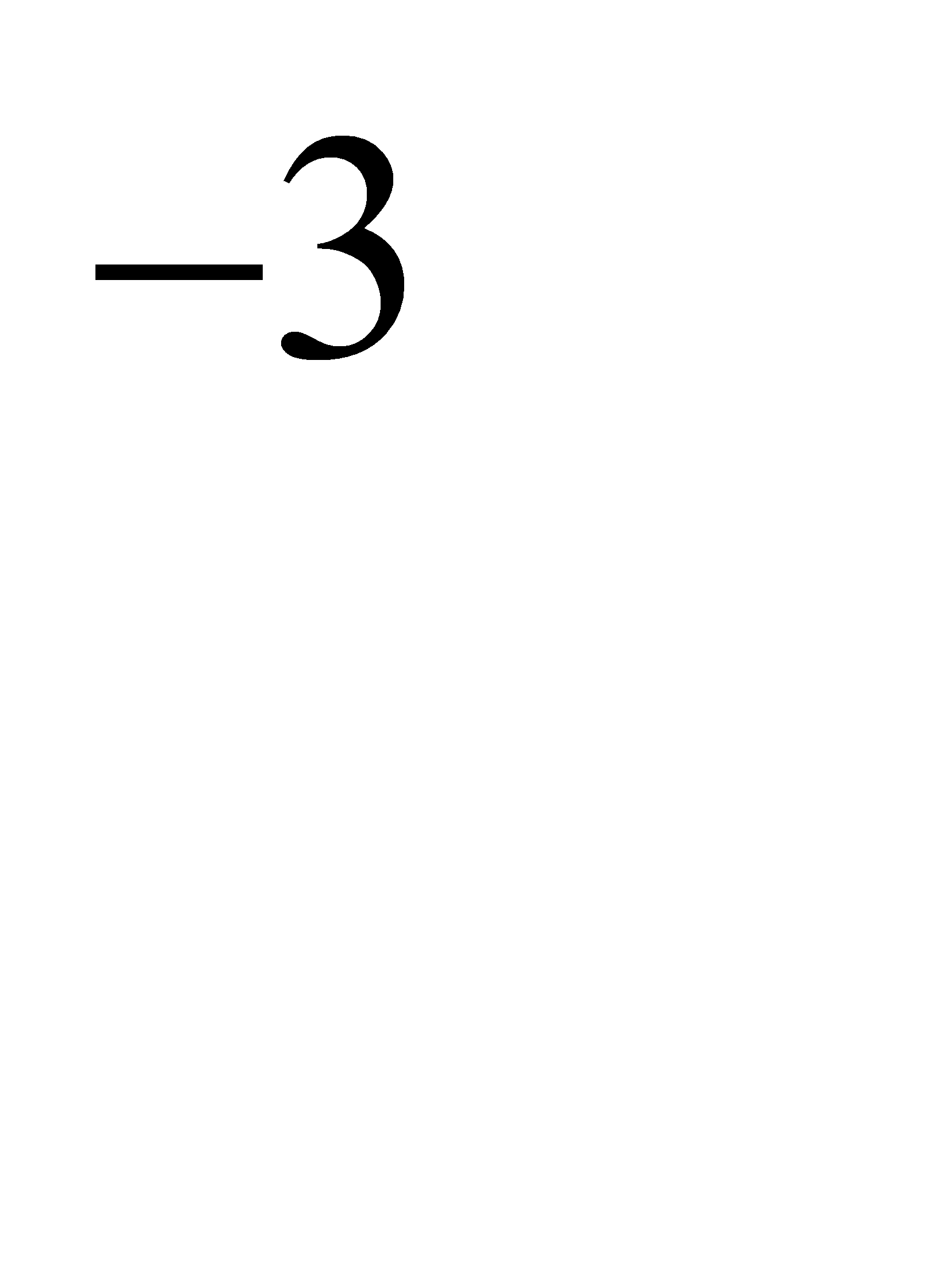 
=0,04979.
Решение:
Число n=1000 слишком велико,а вероятность мала,а рассматриваемые события независимы, поэтому имеет место теорема Пуассона:
где 
, a е 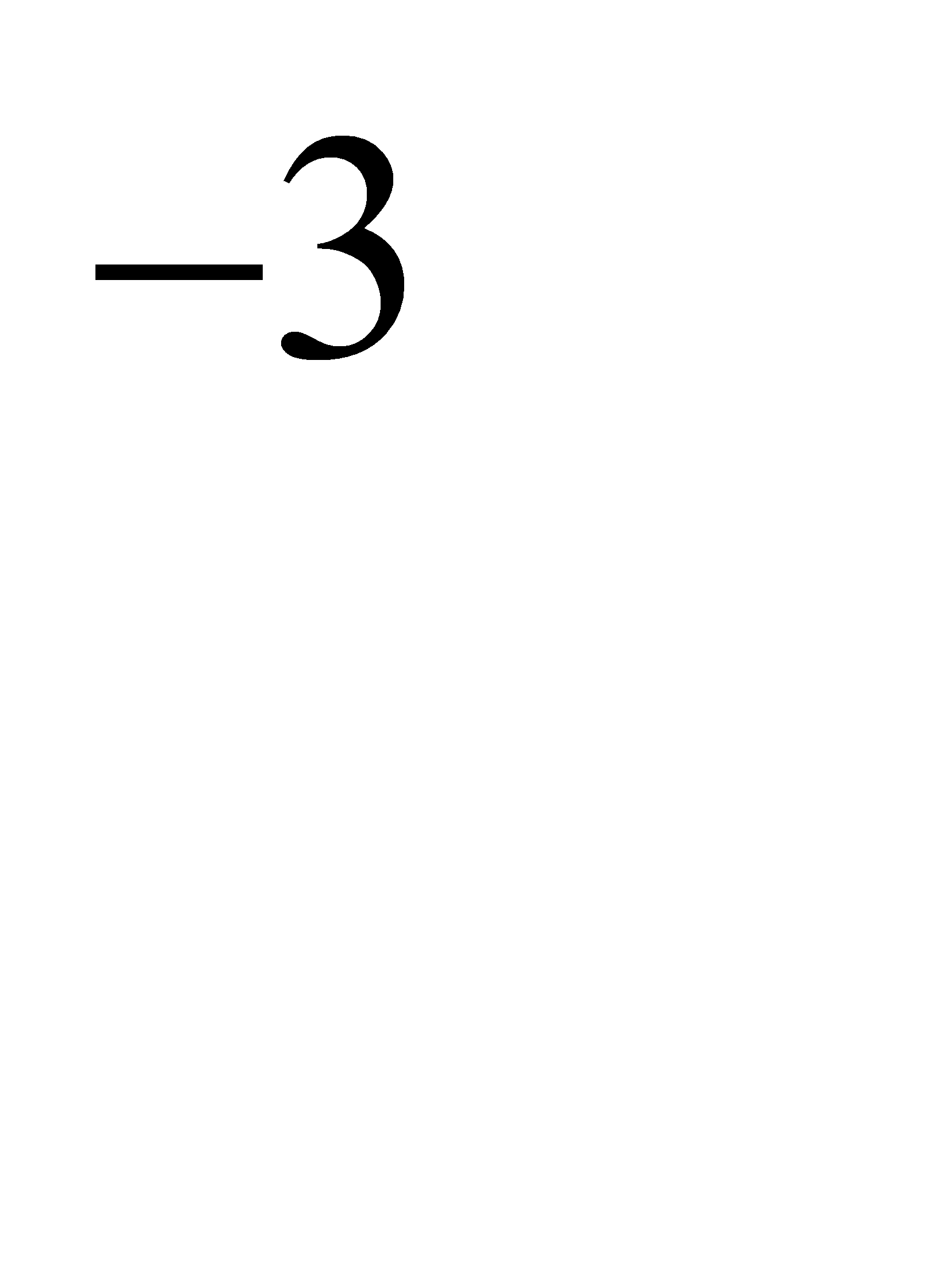=0,04979
Воспользовавшись этой теоремой получим:
а)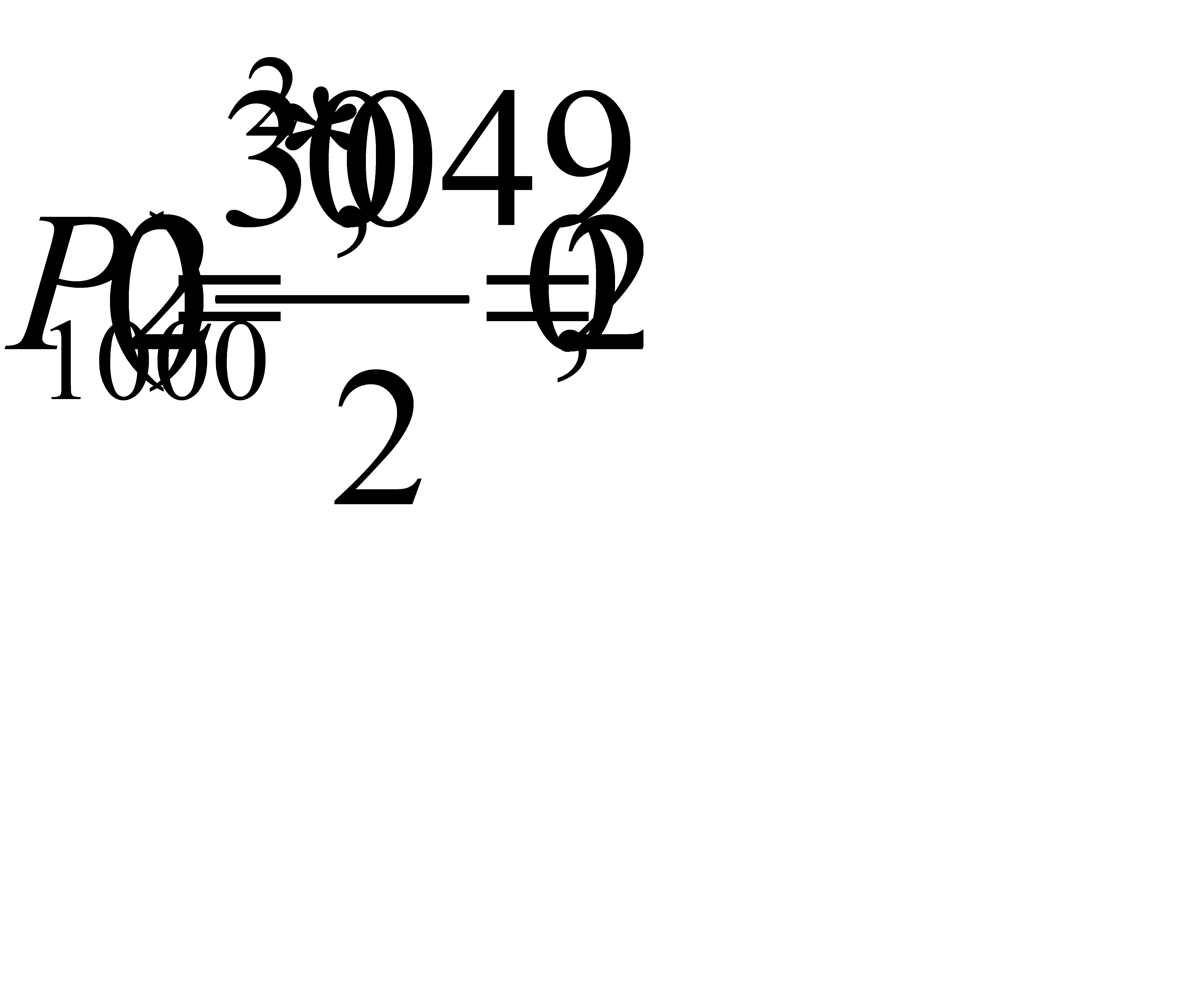 
б) 
в)Эта задача равносильна следующей задаче:
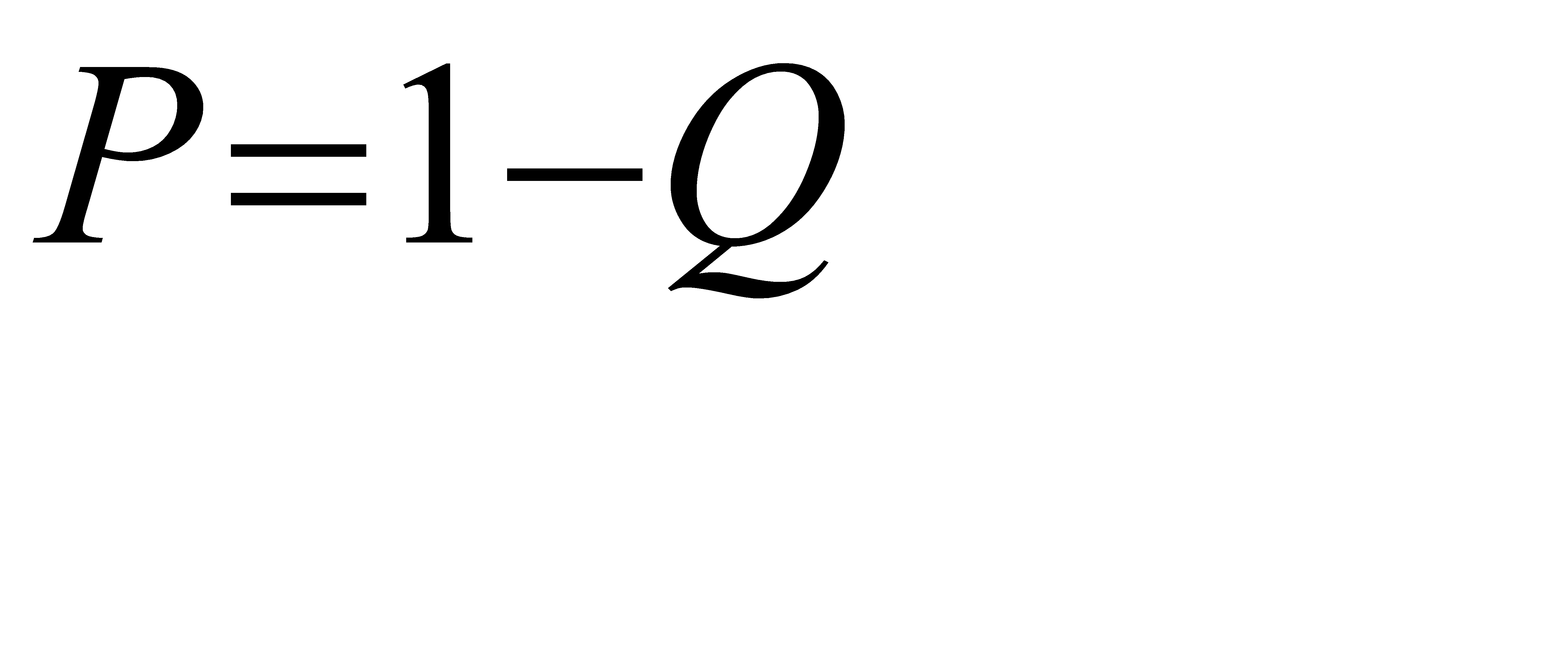где Q= 
=0,224+0,1992=0,423;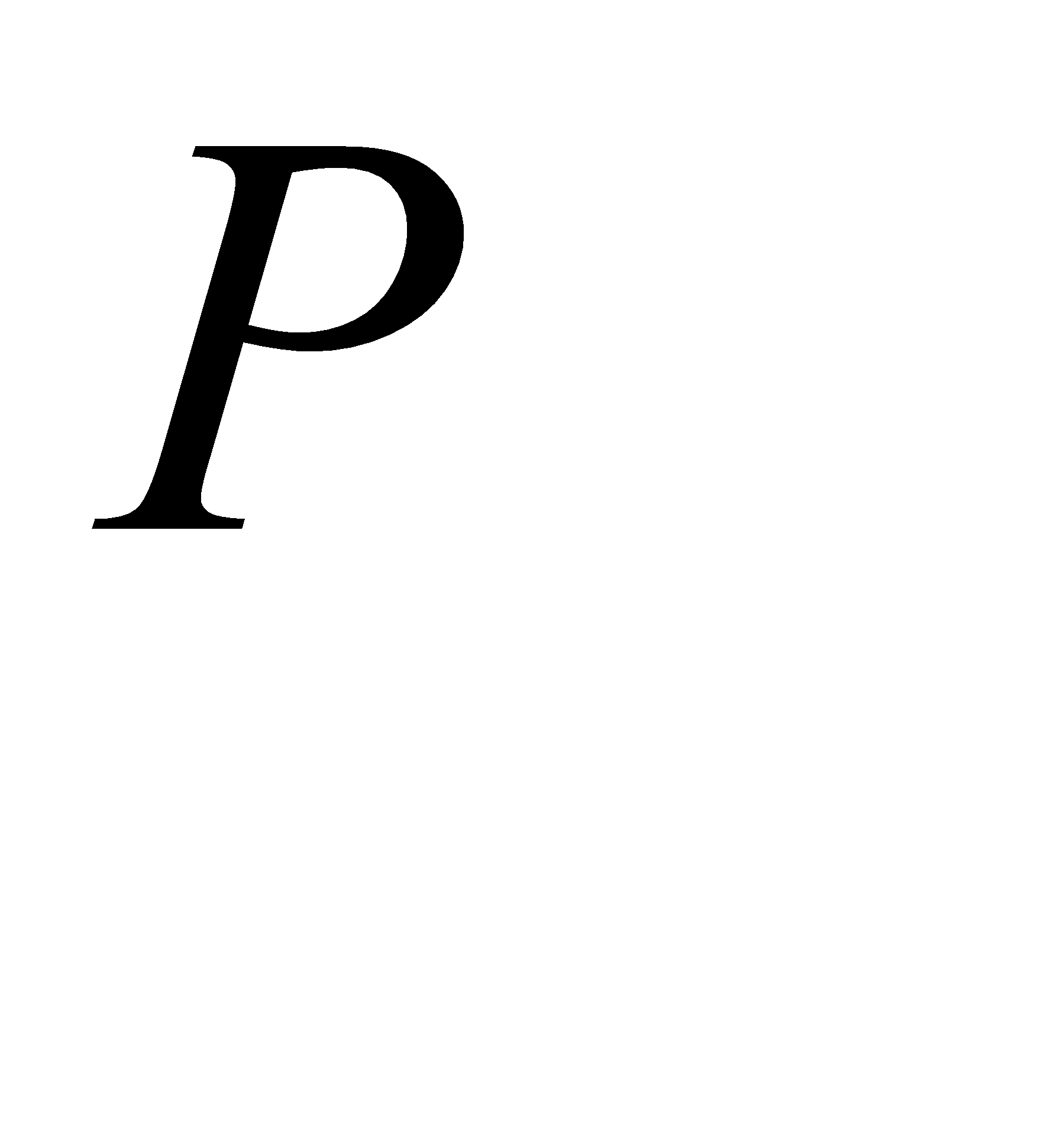 
=1-0,423=0,576
г)Это равносильно задаче Р=1-Q, где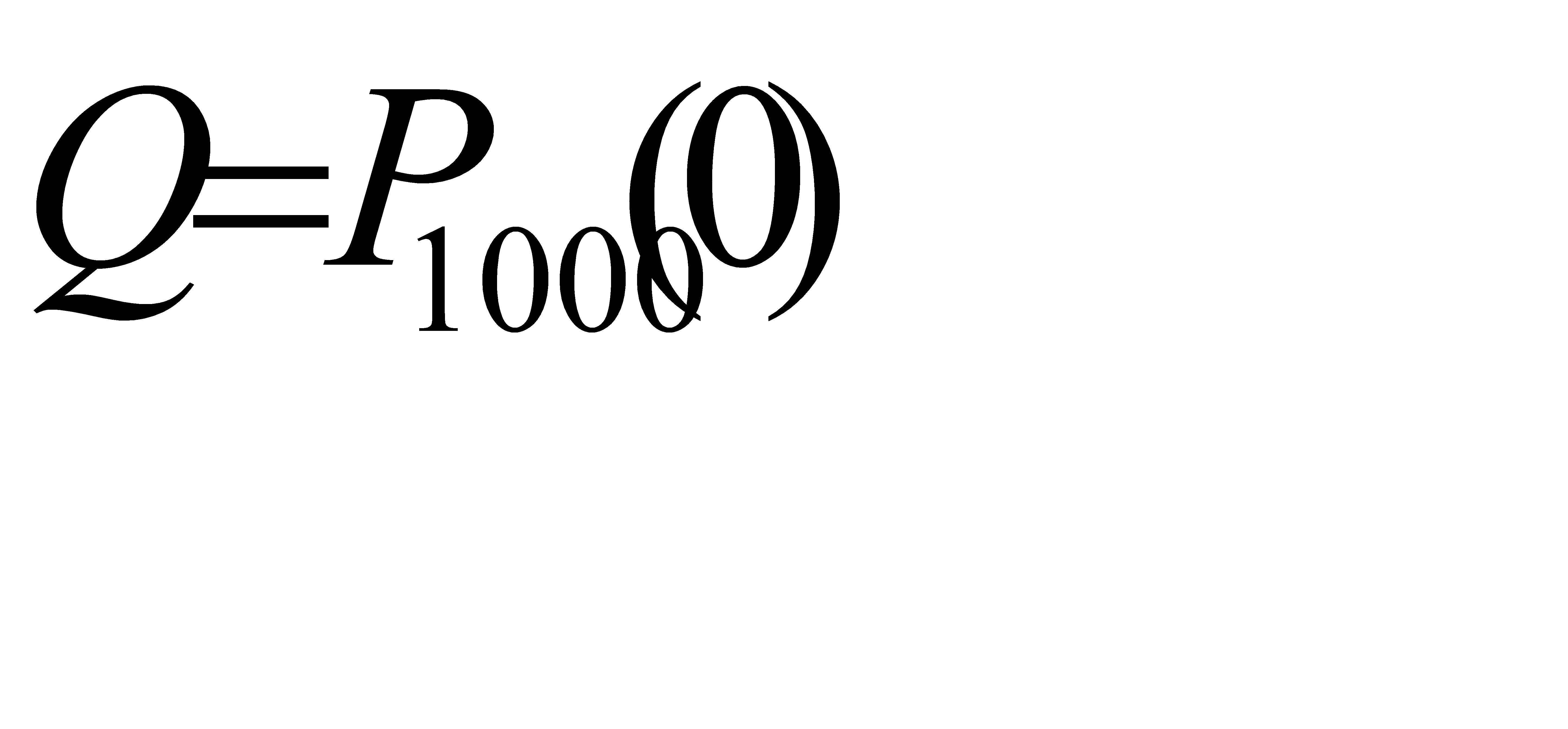 
Ответ: а)0,224; б)0,1992; в)0,576; г)0,95
№181 а) Устройство состоит из большого числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время T. Найти среднее число отказавших за время T элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,98.
