Из уравнения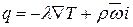 
следует, что плотность теплового потока в любой точке жидкости, для каждого момента времени однозначно определяется, если известны поля температур, удельной энтальпии и скорости.
Для многих задач можно предположить, что жидкость несжимаема, то есть справедливо соотношение для термодинамически идеального газа:
di = cpdT и i = 
cpdT -
Т
уравнение, которое позволяет установить связь между полем температур и полем энтальпии. Чтобы аналитически найти поля температур (энтальпии) и скоростей и определить q, необходимо располагать соответствующими уравнениями.
Уравнение энергии
Это уравнение описывает температурное поле в движущейся жидкости. При его выводе предполагали, что жидкости однородна и изотропна, её физические параметры постоянны, энергия деформации мала по сравнению с изменением внутренней энергии. В итоге получили:
¶Т/¶t + wх¶Т/¶х + wу¶Т/¶у + wz¶Т/¶z = а (¶2Т/¶х2 + ¶2Т/¶у2 + ¶2Т/¶z2) + qv/rср -
- уравнение энергии dT/dt - полная производная от температуры по времени
dT/dt - характеризует изменение температуры во времени в какой-либо точке жидкости, то есть является локальным изменением температуры Т; второй член – характеризует изменение температуры при переходе от точки к точке, то есть является конвективным изменением температуры Т.
Уравнение энергии можно переписать в форме
dT/dt = а Ñ2Т + qv/rср (2)
Если wх = wу = wz = 0, то уравнение энергии переходит в уравнение теплопроводности.
Уравнения движения
Как следует из уравнения (2), температурное поле в движущейся жидкости зависит от составляющих скорости wх, wу, wz. Чтобы сделать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали изменения скорости во времени и пространстве. Такими уравнениями является уравнения движения. Вывод уравнения движения основана на 2-м законе Ньютона: сила равна массе, умноженной на ускорение.
На элемент жидкости действуют 3 силы: 1) сила тяжести, 2) равнодействующая сил давления и 3) равнодействующая сил трения. В общем случае трехмерного движения несжимаемой жидкости с постоянными физическими параметрами скоростное поле описывается тремя уравнениями движения, которые называется уравнениями Навье – Стокса. В векторной форме записи они имеют
набла
rdv/dt = rg - Ñp + mÑ2v,
масса и сила давление сила
ускорение тяжести трения
где m - динамический коэффициент вязкости (Н с/ м2) – численно равен касательной силе, которая действует в любой точке потока в плоскости, ориентированной по течению, если изменение скорости в направлении нормали к этой плоскости dv/dn = 1.
Это уравнение не учитывает зависимость плотности от температуры. В то же время свободное движения жидкости определяется разностью плотностей холодных и нагретых частиц жидкости
С учетом зависимости плотности жидкости от температуры уравнения движущейся жидкости примет вид
|
dv/dt = - gbV - 1/rÑр + uÑ2v,
подъемная сила
где b = r0 - r/r0V – коэффициент объемного расширения (r = r0(1 - bV))
V = T – T0
u = m/r - кинематический коэффициент вязкости, м2/с.
Так как в уравнении движения помимо wх, wу, wz,V входит ещё неизвестная величина р (давление), то система уравнений не является замкнутой.
Необходимо добавить ещё одно уравнение – дифференциальное уравнение сплошности (неразрывности).
Уравнение сплошности
Величина rwх представляет собой кол-во массы, протекающей в единицу времени через единицу поперечного сечения. Избыток массы, вытекающей из рассматриваемого объема, может быть обусловлен изменением плотности в объеме dV и равен изменению массы данного объема во времени ¶r/¶t dudt.
В итоге получено уравнение сплошности для сжимаемых жидкостей:
¶r/¶t + ¶(rwх)/¶х + ¶(rwу)/¶у + ¶(rwz)/¶z = 0
Для несжимаемых жидкостей r = const Þ
¶w x /¶ x +¶w y /¶ y +¶wz/¶z = 0 или div v = 0.
Это уравнение является уравнением сохранения массы. Таким образом, процесс конвективного теплообмена описывается 4-мя уравнениями: 1) уравнением энергии; 2) уравнением движения; 3) уравнением сплошности и уравнением q = qтпр + qконв.
Для решения этих уравнений необходимо задать условие однозначности.
Особенность состоит в следующем. Задание температуры поверхности стенки затруднительно, так как она зависит от процессов теплообмена в стенке и по другую её сторону. Поэтому необходимо к системе дифференциальное уравнений рассматриваемого конвективного теплообмена присоединить дифференциальное уравнения теплопроводности, описывающие передачу тепла в стенке. Затем задать условия сопряжения.
Математическая формулировка задачи может быть упрощена при использовании понятия пограничного слоя. Сложность процессов конвективного теплообмена заставляет при его изучении особенно широко использовать методы экспериментальных исследований. В этом помогает теория подобия. Широко применяются также численные методы расчета.
Лекция 7
