Метод аналогий относится к числу экспериментальных методов исследования процессов теплопроводности. При этом исследование тепловых явлений заменяется изучением аналогичных явлений, так как число их экспериментальное изучение проще осуществить, чем непосредственное исследование тепловых процессов.
Сходство аналогичных явлений состоит в одинаковом характере протекания всех процессов. Математически аналогичные явления описываются формально одинаковыми дифференциальными уравнениями и условиями однозначности. Однако физическое содержание и размерность входящих в них величин различны. Аналогичные явления наталкивают на философские размышления о единстве многих физических явлений, о наличии непознанных пока всеобщих законов физических процессов.
Электротепловая аналогия
Явления теплопроводности и электропроводности описываются следующими уравнениями:
,
где dQ и dI – элементарные потоки теплоты и электричества; прошедшие в единицу времени через площадки dF т, dF э в направлении нормалей n т и n э; U и Т – электрический потенциал и температура; l и s - коэффициенты теплопроводности и электропроводности.
В случае двумерных стационарных задач тепло- и электропроводности и независимых от температуры параметрах l и s соответствующие дифференциальное уравнения имеют вид:
;
.
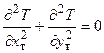Эти уравнения имеют одинаковую структуру. Аналогичные явления должны протекать в геометрически подобных системах. Граничные условия также описываются аналогичными соотношениями.
- l Gr adT = aDT Þ
Þ - Gr ad T = DT/l/a = DT/lт – для тепловой задачи
- Gr ad U = DU/lэ – для электрической задачи.
Записав уравнения и граничные условия в безразмерной форме, получим тождественные уравнения.
Вывод: таким образом, видим, что распределение температуры и электрического потенциала являются подобными, то есть имеет место аналогия.
При исследовании нестационарных процессов для одномерных областей исходные дифференциальное уравнения тепло- и электропроводности имеют вид
¶Т¶t = а ¶Т2/¶хт2; (1) Скорость протекания
процессов зависит
¶U¶t = 1/RэCэ ¶2U/¶xэ2, (2) от а и 1/RэCэ
где Rэ - электрическое сопротивление на единицу длины;
Cэ - электрическая емкость на единицу длины.
Эти коэффициенты, как и коэффициент температуропроводности, не должны зависеть от температуры.
Из уравнений (1) и (2) следует, что аналогия устанавливается, если выполняется условие:
Изменение теплового потока пропорционально изменению теплоемкости системы и изменению температуры:
dQ = cт¶T/¶tт dtт.
Изменение электрическое тока пропорционально емкости и изменению напряжения
dI = cэ ¶U/¶tэ dtэ
Следовательно, в модели теплоемкости могут быть воспроизведены соответствующими электрическими емкостями. Таким образом, можно моделировать процессы теплопроводности на электрических моделях.
При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа:
1) электрические модели повторяют геометрию оригинальной тепловой системы и изготовляются из материала с непрерывной проводимостью (электропроводящее тело или жидкий электролит) – модели с непрерывными параметрами процесса;
2) электрические модели с сосредоточенными параметрами процесса. В них тепловые системы заменяются моделирующими электрическими цепями. Также модели применяются для наиболее сложных явлений.
Для изготовления моделей с непрерывными параметрами используются тонкие листовые электропроводящие материалы. Геометрия модели в точности воспроизводит геометрию исследуемой области. Получить распределение температуры экспериментально весьма затруднительно. Поэтому исследование проводят на модели. Для измерения напряжения используется контактный зонд с нулевым прибором.
Рассмотрим электрическую модель с сосредоточенными параметрами. В этом случае исследуемая тепловая область делится на ряд элементарных объемов. Тем самым исходные дифференциальные уравнения и уравнения, описывающие условия однозначности, заменяются уравнениями в конечных разностях. Моделирующая электрическая цепь представляется в виде отдельных электрических сопротивлений, имитирующих свойства элементов тепловой области. Используются проволочные модели (из реостатного провода).
Для моделирования нестационарного теплового состояния используются RC цепи.
d1/2 d 
2/2 Ra Rэ1 Rэ1 Rэ2 Rэ2
+
Тв, Т1
a; с1 с 2
-
 |
d1 d2
Ra = 1/a;
Rэ1 = d1/2/l1; Rэ2 = d2/2/ l2.
Теплоемкости отдельных слоев воспроизводиться электрическими емкостями с1 и с2. Термические сопротивления поверхности моделируются сопротивлением Ra.
Электрическое моделирование получило широкое развитие. Применяя специальные нелинейные элементы (сопротивления) можно имитировать нелинейные граничные условия (теплообмен излучением).
Тепловая схема замещения. Тепловой закон Ома. Распределенные в пространстве теплофизические параметры заменяются сосредоточенными.
Конвективный теплообмен
Основные понятия и определения
Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью. Под конвекцией теплоты понимают перенос теплоты при перемещении макрочастиц жидкости или газа в пространстве из области с одной температурой в область с другой. Конвекция возможна только в текучей среде, здесь перенос теплоты неразрывно связан с переносом самой среды.
Если в единицу времени через единицу контрольной поверхности нормально к ней проходит масса жидкости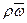 
, кг/(м2с), где 
- скорость, r - плотность жидкости, то вместе с ней переносится энтальпия i, Дж/кг
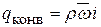
(di – есть элементарное количество теплоты).
Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры. В результате конвективный теплообмен описывается уравнением:
(1)
Здесь 
– локальное (местное) значение плотности теплового потока за счет конвективного теплообмена.
Конвективный теплообмен между потоками жидкости или газа и поверхностью соприкасающегося с ним тела называется конвективной теплоотдачей или теплоотдачей.
При расчетах теплоотдачи используют закон Ньютона – Рихмана:
Поток теплоты dQc от жидкости к элементу поверхности соприкасающегося тела dF прямо пропорционален dF и разности температур DТ = Тс – Тж, где Тс – температура поверхности тела, Тж – температура окружающей жидкости или газа; a - коэффициент теплоотдачи (учитывает конкретные условия процесса теплоотдачи).
a º qс/ Тс – Тж, Вт/(м2К).
В общем случае a зависит от 1) формы размеров тела; 2) режима движения; 3) скорости и температуры жидкости; 4) физических параметров жидкости и т.д. Задача состоит в определении a. Конвективный теплообмен связан с движением жидкости.
Чтобы привести жидкость в движение, к ней необходимо приложить силу. Силы, действующие на какой-либо элемент жидкости, можно разделить на массовые (или объемные) и поверхностные.
Массовыми силами могут быть гравитационные и электрические. Поверхностные силы возникают вследствие действия окружающей жидкости или твердых тел (внешнее давление, силы трения).
Различают свободную и вынужденную конвекцию. В первом случае движение жидкости в рассматриваемом объеме жидкости возникает за счет неоднородности в нем массовых сил. Если жидкость с неоднородным распределением температуры, и, как следствие, с неоднородным распределением плотности, находиться в поле земного тяготения, может возникнуть свободное гравитационное движение. В дальнейшем именно такой вид свободной конвекции мы и будем рассматривать. (В невесомости конвекция затруднена, так как нет гравитационных сил). Где человеку будет теплее – в комнате с Тв = 20° или в космическом корабле в состоянии невесомости при Тв = 20°? – в космосе, так как конвективная теплоотдача затруднена.
Вынужденное движение рассматриваемого объема жидкости происходит под действием внешних поверхностных сил, приложенных на его границах, за счет предварительно сообщенной кинетической энергии (например, за счет насоса, вентиляции, ветра).
Вынужденное движение в общем случае сопровождается свободным движением. При больших скоростях вынужденного движения влияние свободной конвекции пренебрежимо мало.
Стационарным считается процесс, когда скорости и температуры в любой точке жидкости не изменяются во времени.
