Для полного математического описания процесса кроме уравнения теплопроводности необходимы условия однозначности:
- геометрические условия;
- физические условия (l, с, r, qv,…);
- временные (начальные) условия Т = f(x, y, z) при t = 0;
- граничные условия – характеризуют условия взаимодействия с окружающей средой.
Граничные условия:
1-го рода - задается распределение температур на поверхности
Tc = f (x, y, z, t).
2-го рода - задается значения теплового потока на поверхности. Пример - пленка резистора.
qп = f (x, y, z, t) или qп = const.
3-го рода – задается температура жидкой среды и закон теплообмена между поверхностью и окружающей средой (закон Ньютона – Рихмана).
q = a(Тс – Тж),
где a - коэффициент теплоотдачи (в общем случае зависит от температуры)
a(Тс – Тж) = -l(¶Т/¶n)с
или - (¶Т/¶n)с = a/l(Тс – Тж) – частный случай закона сохранения энергии
4-го рода – условия сопряженности – условия равенства температур и тепловых потоков по обе стороны от границы раздела.
l1(¶T1/¶n)г = l2(¶T2/¶n)г + qs(xг, yг, zг, t),
t1 (xг, yг, zг, t) = t2 (xг, yг, zг, t),
где qs – источник теплоты на поверхности границы
Поставленная таким образом задача решается аналитически, численно или экспериментально.
Теплопроводность в стационарном режиме
При установившемся (стационарном) тепловом режиме температура тела во времени остается постоянной. Если внутренние источники теплоты отсутствует, то:
.
Рассмотрим теплопроводность в телах простейшей формы.
Плоская стенка (qv = 0). Граничные условия 1-го рода
Так как dx << dy (dz), то теплоотводом по у и z пренебрегаем.
Дифференциальное уравнение:
.
Граничные условия:
при х = 0 Т = Тс1
при х = d Т = Тс2
Нужно определить: поле температур и q.
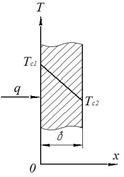
Рис. 3 Однородная плоская стенка
Закон распределения температуры по толщине стенки (рис. 3) находится после двойного интегрирования:
.
Температура в данном случае изменяется по линейному закону.
Постоянные интегрирования с1 и с2 определяются из граничных условий:
с2 = Тс1, с1 = Тс2/d.
.
Плотность теплового потока выразится:
.
Термическое сопротивление стенки:
Rт =l/d.
Многослойная стенка
Складываем левую и правую части уравнений.
Таким образом, для любой многослойной стенки, температурный напор можно определить:
.
Тепловой поток, проходящий через многослойную стенку:
,
где 
– полное термическое сопротивление многослойной стенки.
Переменный коэффициент теплопроводности
Пусть для плоской стенки l = l0(1 + bТ),
где l0 – значение коэффициента теплопроводности при 0°С.
На основании закона Фурье
. (а)
Разделяя переменные и интегрируя в пределах от х = 0 до х = d в интервале температур от Тс1 до Тс2, получаем:
.
Среднеинтегральное значение коэффициента теплопроводности:
.
Тогда, плотность теплового потока выразится:
.
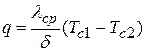Интегрируя (а) в пределах от х = 0 до любой координаты х и в интервале температур от Тс1 до Т, получаем:
Температура изменяется по кривой:
.
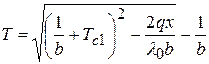Плоская стенка (qv = 0). Граничные условия третьего рода (теплопередача)
Передача тепла из одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей.
Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.
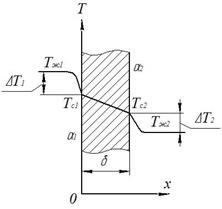
Рис. 4 Теплопередача через плоскую стенку
На рис. 4 показана - плоская стенка толщиной d; Тж1 и Тж2 - температуры окружающей среды; a1 и a2 - коэффициенты теплоотдачи (постоянные). Температура изменения только в направлении, перпендикулярном плоскости стенки.
Необходимо найти: тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки.
Плотность теплового потока от горячей жидкости к стенке определяется уравнением:
. (1)
При стационарном режиме тот же тепловой поток пройдет путем теплопроводности через твердую стенку:
. (2)
Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи:
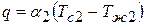. (3)
Эти уравнения можно написать в виде:
.
Отсюда плотность теплового потока, Вт/м2:
.
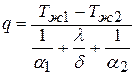Коэффициент теплопередачи, Вт/(м2 К):
.
Он характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку.
Термическое сопротивление теплопередачи:
.
Плотность теплового потока выразится:
.
Тепловой поток:
.
Температуры поверхностей однородной стенки можно найти из уравнений (1), (2), (3):
;
или
.
(аналогично с электрическим током и напряжением)
Цилиндрическая стенка (qv = 0)
Уравнение теплопроводности в цилиндрических координатах:
Рис. 5 Теплопроводность цилиндрической стенки
Найти: 1) распределение температур; 2) тепловой поток
Уравнение теплопроводности:
.
Граничные условия 1-го рода:
при r = r1 Т = Тс1;
при r = r2 Т = Тс2.
Введем новую переменную 
Þ
Þ 
Интегрируем: 
Þ 
.
Потенцируя и переходя к первоначальной переменной
Þ 
.
После интегрирования получаем:
.
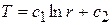Из граничных условий находим постоянные интегрирования:
; 
.
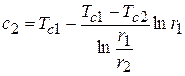Уравнение температурного поля:
.
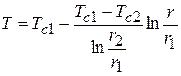Плотность теплового потока зависит от радиуса (гиперболическая кривая) (рис. 5):
.
Тепловой поток не зависит от радиуса, так как:
,
где 
- площадь боковой поверхности цилиндра.
Линейная плотность теплового потока:
.
Термическое сопротивление цилиндрической стенки:
При 
линейна плотность теплового потока выразится, как:
,
где 
.
Температурное поле находим из уравнения закона Фурье.
(разделяем переменные и интегрируем от r = r1 до r и от Т = Тс1 до Т).
.
Цилиндрическая стенка (qv = 0). Граничные условия третьего рода (теплопередача).
Рассмотрим однородную цилиндрическую стенку (трубку) с постоянным коэффициентом теплопроводности l (рис. 6).
Необходимо найти: ql и Тс1
Предполагаем, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь. При установившемся тепловом режиме количество теплоты, которое будет передаваться от горячей среды к поверхности стенки, проходить через стенку и отдаваться от стенки к холодной жидкости, будет одно и то же.
Рис. 6 Теплопередача через однородную цилиндрическую стенку
Тепловой поток при теплопередаче через цилиндрическую стенку можно выразить:
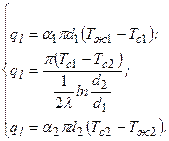
Выразим температурные напоры:
Складывая уравнения, получаем температурный напор:
.
Откуда линейная плотность теплового потока находится:
.
Линейный коэффициент теплопередачи:
, Вт/(м∙К)
Линейная плотность теплового потока:
.
Линейное термическое сопротивление:
.
Отметим, что линейное термическое сопротивление зависит не только от коэффициентов теплоотдачи a1, a2, но и от соответствующих диаметров.
Критический диаметр цилиндрической стенки
Рассмотрим влияние изменения наружного диаметра на термическое сопротивление однородной цилиндрической стенки
.
При постоянных значениях a1, d1, a2, l полное термическое сопротивление теплопередачи цилиндрической стенки будет зависеть от внешнего диаметра d2.
Причем термическое сопротивление теплопроводности 
с увеличением d2 будет возрастать, а термическое сопротивление теплоотдачи 
будет уменьшаться (рис. 7).
Для того чтобы выяснить, как будет изменяться Rl при изменении толщины цилиндрической стенки, исследуем Rl как функцию d2.
Возьмем производную от Rl по d2 и приравняем нулю:
.
Откуда:
.
При данном значении диаметра термическое сопротивление теплопередачи будет минимальным.
Рис. 7 Зависимость термического сопротивления цилиндрической стенки от d2
Значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром
.
Эти соображения необходимо учитывать при выборе тепловой изоляции цилиндрических аппаратов и трубопроводов. При d2 < dкр с увеличением d2 полное термическое сопротивление теплопередачи снижается, так как увеличение d2 наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки. То есть в этом случае дополнительная теплоизоляция может увеличить потери тепла.
Передача теплоты через шаровую стенку
Пусть имеется полный шар с радиусами r1 и r2, постоянным коэффициентом теплопроводности l и заданными равномерно распределенными температурами поверхностей Tс1 и Tс2 (рис. 8).
Уравнение Лапласа в сферической системе координат имеет вид:
.
Рис. 8 Теплопроводность однородной шаровой стенки
В данном случае Т не зависит от q и y:
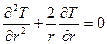. (1)
Пусть заданы граничные условия 1-го рода:
при r = r1 T = T1;
при r = r 2 T = T2.
Необходимо найти: распределение температуры по толщине сферической стенки.
Представим уравнение (1) в форме
. (2)
После 1-го интегрирования (2) получим
или 
.
После 2-го интегрирования:
.
Используя граничные условия, найдем с1 и с2:
; при r = r1;
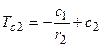; при r = r2.
Решая эти уравнения относительно с1 и c2, получим:
;
.
Температурное поле:
.
Температура Т(r) изменяется по толщине стенки по гиперболе.
