Рассмотрим задачи без внутренних источников тепла. Аналитическое описание процесса теплопроводности включает в себя дифференциальное уравнение и условия однозначности.
Дифференциальное уравнение теплопроводности при отсутствии внутренних источников теплоты имеет вид:
, (1)
где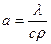 
- коэффициент температуропроводности, м2/с (характеризует скорость изменения температуры).
Условия однозначности задаются в виде:
- физических параметров l, с, r;
- формы и геометрических размеров объекта l0, l1,…, ln; (2)
- температуры тела в начальный момент времени: при t = 0 Т0 = f (x, y, z).
Граничные условия могут быть заданы в виде граничных условий 3-го рода:
.
Дифференциальное уравнение совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение её заключается в отыскании функции
Т = f (x, y, z, t, а, Т0, Тж, l0, l1,… ln),
которая удовлетворяла бы уравнению (1) и условиям (2).
Рассмотрим подробно решение задачи охлаждения плоской однородной стенки. Изучив метод решения задачи, можно понять принцип решения задач и для тел другой геометрической конфигурации.
Охлаждение (нагревание) неограниченной пластины
Дана пластина толщиной 2 d. Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину считают неограниченной. Коэффициент теплоотдачи a одинаков для всех точек пластины (рис. 12). Изменение 
температуры происходит в направлении х. В пространстве задача является одномерной.
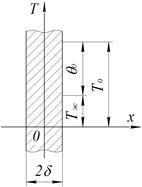
Рис. 12 К охлаждению плоской неограниченной пластины. При τ = 0 задано Т0=const и θ0=const.
Начальное распределение температуры задано некоторой функцией
.
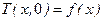Охлаждение происходит в среде с постоянной температурой Тж = const. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды Тж, то есть
.
Дифференциальное уравнение теплопроводности имеет вид:
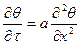. (1)
Начальные условия: при t = 0 θ = θ 0 = f (x) – Тж = F(х).
При заданных условиях охлаждения задача становиться симметричной и начало координат удобно поместить на оси пластины.
При этом граничные условия:
а) на оси пластины при х = 0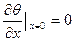 
;
б) на поверхности пластины при х = d 
.
Для решения дифференциального уравнения применяем метод разделения переменных. При этом решение дифференциальное уравнения ищем в виде произведения двух функций, из которых одна является функцией только времени t, а другая – только х:
.
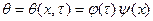После подстановки этого выражения в уравнение (1), получим:
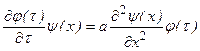или
.
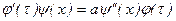В этом уравнение легко разделяются переменные
. (2)
Левая часть – функция только t, правая только х. Если зафиксировать аргумент х и менять только t, то при любом его значении левая часть уравнения (2) равна постоянной величине, стоящей в правой части, то есть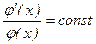 
. Аналогично при фиксации t и изменении х правая часть уравнения для любого значения х должна равняться постоянной левой части, которая зависит только от t, то есть 
.
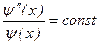Так как равенство (2) должно иметь место при любых значениях х и t, то обе его части должны быть равны одной и той же постоянной величине.
.
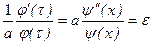Нетривиальное решение для функции y(х) только при e < 0. Положим, что e = - k2 :
.
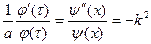Система обыкновенных дифференциальных уравнений:
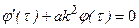; (3)
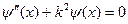. (4)
Постоянная k определяется из граничных условий, а знак «минус» выбирается из физических соображений. Для тепловых процессов, стремящихся к тепловому равновесию, знак может быть только минус.
Уравнению (3) удовлетворяет функция 
.
Уравнение (4) – функция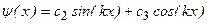 
.
В результате получили общее решение
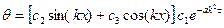. (5)
Для того чтобы уравнение (5) было решением поставленной задачи, его нужно подчинить начальным и граничным условиям.
При х = 0 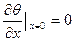, находим
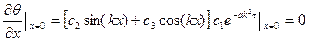Þ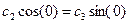 
Þ с2 = 0
Следовательно, частное решение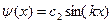 
– должно быть отброшено как не удовлетворяющее граничным условиям.
Если учесть, что с2 = 0 и обозначить с1с3 = А, то уравнение (5) примет вид:
.
При х = d 
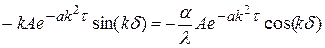Þ 
½ умножив и разделив на d, получим:
,
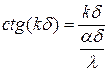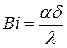- число Био – безразмерный показатель (характеризует соотношения внутреннего и внешнего тепловых сопротивлений).
Если обозначить kd = m, то:
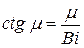(1)
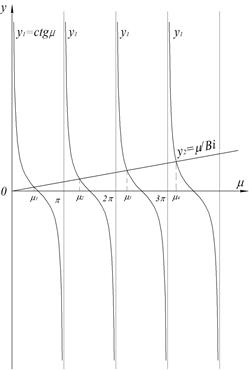
Из анализа этого уравнения следует, что при каждом значении Вi существует бесконечное множество решений. Наиболее просто это равнение решается графическим способом.
Рис. 13 К решению уравнения (1).
Обозначим через y1 = сtg m,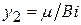 
.
Пересечение котангенсоиды у1 с прямой у2 дает бесконечное множество корней характеристического уравнения m1 < m2 < m3 <…< mn (рис. 13).
Каждому значению Bi отвечает своя совокупность корней уравнения (1). Первые четыре корня такого уравнения приводятся в таблице.
При Вi ® ¥ (внутреннее сопротивление велико по сравнению с внешним) у2 = 0 – совпадает с осью х и корни будут равны:
m1 = p/2; m2 = 3p/2; mn = (2n-1) p/2
При Вi ® 0 (внутреннее сопротивление мало по сравнению с внешним) прямая 
совпадает с осью ординат и тангенс угла наклона стремиться к ¥ ® корни равны:
m1 = 0; m2 = p,…, mn = (n-1) p.
Следовательно, каждому найденному значению корня m будет соответствовать свое частное распределение температур:
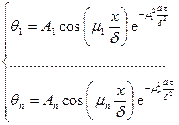, здесь мы учли, что k = μ/δ.
Путем наложения бесконечного числа таких распределений температур можно получить истинное распределение:
. (а)
Постоянная Аn находится из начальных условий:
.
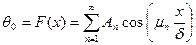Это есть разложение четной функции в ряд Фурье. Есть специальные формулы для определения коэффициентов Аn. .
Если в начальный момент времени t = 0 температура в любой точке пластины распределена равномерно (Т0 – Тж = θ0 = const), то:
.
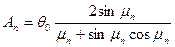Подставляя Аn в выражение (а), получим
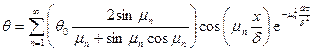. (б)
Уравнение температурного поля (б) целесообразно представить в безразмерной форме. Для этого разделим правую и левую части уравнения на θ0 (начальная разность температур). При этом обозначим: Dn = Аn / θ0. Получим:
, (в)
где Q = θ/θ0 – безразмерная температура; Х = х/d - безразмерная координата; Fo =aτ/δ2 – число Фурье, представляющее собой безразмерное время; Dn = Аn / θ0 – безразмерный коэффициент.
Получим, что температура каждой точки во времени изменяется по экспоненциальному закону. Распределение температуры по координате х (по толщине) – имеет вид косинусоиды с максимумом в центре пластины.
