В рассматриваемых ранее задачах внутренние источники теплоты отсутствовали. Однако в ряде случаев внутри объектов исследования могут протекать процессы, в результате которых будет выделяться или поглощаться теплота. Примерами таких процессов могут служить: выделение джоулевой теплоты при прохождении электрического тока P = I2R; диэлектрические потери в диэлектриках Pg = cwu2 tgd, находящихся в электрическом поле; выделение или поглощение теплоты при протекании химических реакций.
При исследовании переноса теплоты в таких случаях важно знать интенсивность объемного выделения (поглощения) теплоты, которая количественно характеризуется мощностью внутренних источников теплоты qv, Вт/м3. Если величина qv > 0, то говорят, что в теле имеются положительные источники теплоты. При qv < 0 имеются отрицательные источники (стоки) теплоты.
Теплопроводность однородной пластины
Рассмотрим длинную пластину толщиной 2 d. Источники тепла равномерно распределены по объему и равны qv = const. Условия охлаждения с обеих сторон пластины одинаковые (Tж = const, a = const). При указанных условиях температура пластины будет изменяться только вдоль оси х (рис. 9).
Рис. 9 Теплопроводность пластины при наличии внутренних источников тепла
Необходимо найти: распределение температур в пластине и количество теплоты, отданное в окружающую среду.
Дифференциальное уравнение принимает вид:
. (1)
Граничные условия:
при х = ± d 
; (2)
при х = 0 
. (3)
В силу симметрии поля температур относительно плоскости х = 0 рассматриваем только половину пластины.
После интегрирования (1) получим:
; (4)
.(5)
Температурная зависимость по толщине пластины имеет вид параболы.
Постоянные с1 и с2 определяются из граничных условий.
При х = 0 из выражения (2) находим c1 = 0.
При х = d из выражения (4) находим 
и подставляем в (2):
,
откуда:
.
Тогда из (5) можно найти с2:
Þ 
.
Уравнение температурного поля примет вид:
.(6)
В данной задаче (в отличие от аналогичной без тепловыделения) тепловой поток изменяется вдоль оси х (см. уравнение (4)):
.
При х = 0 и q = 0. При х=d:
.
Общее количество теплоты, отдаваемое всей поверхностью в единицу времени (вся поверхность F равна двум боковым поверхностям F1):
.
Из уравнения (5) следует, что температура в плоской стенке в случае симметричной задачи распределяется по параболическому закону.
Теплопроводность однородного цилиндрического стержня
Рассмотрим круглый цилиндр, радиус которого мал по сравнению с длиной цилиндра. При этих условиях температура будет изменяться только вдоль радиуса r (рис. 10). Внутренние источники теплоты равномерно распределены по объему стержня.
Рис. 10 Теплопроводность однородного цилиндрического стержня при наличии внутренних источников тепла
Как и для пластины, задача будет одномерной и симметричной.
Уравнение имеет вид:
. (1)
Граничные условия:
при r = 0 
;
при r = r0 
.
Необходимо найти: уравнение температурного поля и тепловой поток.
Проведем замену переменных 
, тогда уравнение (1) примет вид:
(2)
Умножим выражение (2) на rdr и получим:
. (3)
Первые два слагаемых выражения (3) являются:
.
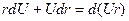Тогда выражение (3) можно представить в виде:
.
После интегрирования получим:
. (4)
Разделим выражение на r, получим:
.
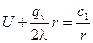Вернувшись к замене, получим:
. (5)
После второго интегрирования получим:
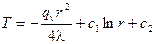. (6)
Определим с1 и с2 из граничных условий.
При r = 0 находим из (5), что с1 = 0.
При r = r0 находим из (5), что 
и подставляем в граничные условия:
.
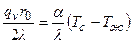Откуда:
.
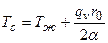Из (6) находим с2:
;
.
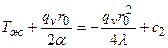Уравнение температурного поля:
.
Распределение температуры в круглом стержне подчиняется параболическому закону.
Плотность теплового потока на поверхности цилиндра:
.
Полный тепловой поток:
.
Лекция № 4
