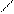Теплоотдача при ламинарном пограничном слое

Для расчета теплоотдачи при ламинарном слое используем интегральное уравнение теплового потока для теплового пограничного слоя:

Чтобы рассчитать теплоотдачу, необходимо знать распределение скорости в слое. В случае ламинарного пограничного слоя распределение скорости в нем близко к параболе (кубическая парабола):

w_х = а + bу + су² + dу³ (a)

Уравнение распределения скорости должно удовлетворять граничным условиям.

При у = 0 w_х = 0 (условие «прилипания»), полагаем также, что (¶²w_х/¶у²) = 0.

При у = d (на внешней границе слоя) w₀ = w_х и (¶w_х/¶у) = 0.

Уравнение (а) будет удовлетворять этим требованиям, если

а = 0; с = 0;b = 3/2w₀/d; d = - 1/2w₀/d³.

Распределение скорости при этом примет вид:

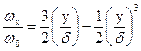(б)

При распределении скорости согласно (б) из интегрального уравнения импульсов

 

-

можно получить, что толщина гидродинамического пограничного слоя определяется выражением:

или в безразмерной форме

Таким образом, толщина d изменяется пропорционально корню квадратному из расстояния от переднего края пластины до данной точки. Чем больше вязкость, тем толще d. Чем выше скорость – тем меньше (тоньше) слой d.

Пограничные условия для температур:

При у = 0 u (здесь и ниже принято u = Т – Тс) и (¶u/¶у)_у=0 = const и Þ (¶²u/¶у²) = 0, если учесть, что в жидкости, непосредственно прилегающей к плоской стенке, теплота передается по у только теплопроводностью.

При у = k (на внешней границе теплового слоя) u = u₀ = const и (¶u/¶у)_у=k = 0.

То есть граничные условия получились аналогичны принятым ранее условиям для гидродинамического пограничного слоя.

В результате получаем, что распределение температуры описывается уравнением, аналогичным по форме записи уравнению распределения скорости

u/u₀ = 1,5 (у/k) – 0,5 (у/k)³ (А)

После подстановки в интегральное уравнение теплового потока и упрощений получили:

,

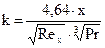где Re_х = w₀х/n; Рr = n/а.

Тогда – то есть отношение k/d не зависит от х, а зависит только от числа Рr.

Для капельных жидкостей Рr ³ 1, Þ d³ k.

Для газов Рr = 0,6 – 1 (для воздуха Рr» 0,7). При этом k>d.

Определим коэффициент теплоотдачи из уравнения , Þ _у=0 зная, что (это следует из производной), опуская знак ²-² получим:

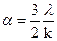(а)

Коэффициент теплоотдачи обратно пропорционален толщине пограничного слоя (чем меньше толщина k, тем больше a Þ лучше теплоотдачи).

Уравнение (а) можно привести к безразмерному виду (умножив левую и правую части на х/l и подставляя значение ):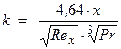

(б)

Здесь Nu_x = ax/l = a /l x/ = Nu_еX; Re_x = w₀x/n = w₀ /n x/ = Re_еX; Pr = n/a; – длина пластины вдоль потока.

Формула (б) справедлива только при условии, что температура поверхности пластины постоянна, физические параметры жидкости, не зависят от температуры и в начале пластины нет необогреваемого участка.

Коэффициент теплоотдачи капельной жидкости зависит от рода жидкости, ее температуры, направления теплового потока. Особенно существенное влияние оказывает зависимость вязкости от температуры. При охлаждении жидкости, вязкость увеличивается, течение замедляется. Поэтому для жидкостей вводится поправка (Pr_ж/ Pr_с)^0,25, которая учитывает влияние на теплообмен изменения вязкости. Для (Pr_ж/ Pr_с)^0,25 Þ 1.

Индекс «с» - означает, что Pr_с вычислен при температуре стенки; «ж» - при температуре жидкости вдали от стенки.

 

Переход ламинарного течения в турбулентное

 

 

1 – ламинарный пограничный слой; 2 – переходная область; 3 – турбулентный пограничный слой; 4 – вязкий (ламинарный) подслой.

 

Переход ламинарного течения в турбулентное происходит на некотором участке. Течение на этом участке имеет нестабильный характер и называется переходным.

Законы теплообмена при ламинарном и турбулентном режимах различны, поэтому определение их границ имеет большое значение.

О режиме течения судят по критическим значениям числа Re:

Re _кр1 = w₀х_кр1/n и Re _кр2 = w₀х_кр2/n,

где х – продольная координата, отсчитываемая от передней кромки поверхности. Зная Re _кр1 и Re _кр2 можно определить х_кр1 и х_кр2, которые определяют соответственно начало разрушения ламинарного слоя и появления устойчивого турбулентного течения. Из опытных данных получено, что

Re _кр = 10⁴ - 4×10⁶

На переход влияют такие характеристики внешнего источника, как степень турбулентности, масштаб турбулентности. При ускорении потока переход затягивается, при замедлении - наступает при меньших значениях х (или Re _х).

Кроме параметров внешнего потока на переход из ламинарного течения в турбулентное влияют параметры, связанные с омываемым теплом. Значения Re _кр1 и Re _кр2 зависят:

1) от интенсивности теплообмена;

2) от волнистости, шероховатости поверхности;

3) обтекаемости передней кромки пластины;

4) вибрации тела.

На рис. представлена зависимость критических чисел Рейнольдса от степени турбулентности набегающего потока

,

где v¢²_x, v¢²_y, v¢²_z – средние во времени квадраты трех составляющих пульсации скорости; w₀ – скорость внешнего потока.

При сравнительно малых значениях Tu переход не зависит от степени турбулентности внешнего потока, а определяется характеристиками самого ламинарного слоя (его устойчивостью).

Увеличение Tu приводит к уменьшению Re _кр.

На практике сечение перехода можно определить по изменению осредненной во времени v_х (у). При турбулентном течении v_х резко увеличивается вблизи стенки, на удалении от нее v_х (у) становится более выровненной. Выравнивание объясняется турбулентным переносом кол-ва движения.

Теплоотдача при турбулентном пограничном слое

 

Перенос теплоты и количества движения поперек турбулентного пограничного слоя можно описать уравнениями:

q = - (l + l_т)× = - (l + rс_рe_q)× ,

S = (m + m_т)× = (m + re_s)× ,

где S – касательная сила трения; l_т, m_т – коэффициенты турбулентного переноса теплоты и кол-во движения; e_q = l_т/rс_р,e_s = m_т/r - кинематические коэффициенты турбулентного переноса теплоты и кол-ва движения.

Эти уравнения можно переписать в виде:

q = - l(1 + )× (1)

S = rn(1 + e_s/n)× (2)

Здесь Pr _т = e_s/e_q; Pr = n/а = n/l/сr

Величину Pr _т – называется турбулентным числом Прандтля. С учетом (1) и (2) дифференциальное уравнение энергии и движения для турбулентного пограничного слоя примут вид

= а [(1 + ) ], (3)

= n [(1 + e_s/n) ]. (4)

Если Pr = 1 (а = n) и Pr _т = 1, то уравнения (3) и (4) идентичны. В этом случае при идентичных граничных условиях поля температуры u и скорости v_х будут подобны.

Для того, чтобы проинтегрировать уравнение (3) и (4), необходимо иметь сведения о коэффициентах турбулентного переноса теплоты e_s и e_q.

Опыты показывают сложность движения в турбулентном слое:

А d Б II dп I

Рис. Турбулентный пограничный слой А – внешняя область; Б – пристенная область (I – вязкий подслой (ламинарный); II – промежуточный слой). Пульсации, особенно крупномасштабные (низкочастотные), проникают в вязкий подслой, где их течение регламентируется

вязкими силами. Поэтому граница подслоя четко не определена. Наиболее высокая интенсивность турбулентности наблюдается в пристенной области Б. Внешняя граница турбулентного пограничного слоя непрерывно пульсирует. В зависимости от области характер переноса теплоты различен.

Аналогично вязкому подслою непосредственно у стенки наблюдается тепловой подслой.

Он характеризуется преобладанием теплоты теплопроводностью над турбулентным переносом.

При Pr = 1 толщина вязкого подслоя d_п и теплового k_п совпадают.

Поскольку в тепловом подслое перенос теплоты определяется теплопроводностью, то изменение температуры по его толщине описывается уравнением прямой (как для плоской стенки). В остальной части турбулентного слоя температура распределяется по логарифмическому закону.

Зная распределение скоростей и температуры, можно рассчитать теплоотдачу с помощью интегральных уравнений теплового потока и импульса.

На основе эмпирических данных и вычислений был получен безразмерный комплекс – число Стантона

St º

При Pr = 1 и Pr_т = 1 – получаем аналогию переноса теплоты и кол-ва движения. На основе опытных данных получена формула

Nu_жх = 0,0296 Re _жх^0,8× Pr _ж^0,43(Pr _ж/ Pr _с)^0,25

За определяющую принята температура жидкости вдали от тела Т₀ (за исключением Pr_с, выбираемого по температуре Т_с – стенки). Определяющим размером является координата х, отсчитываемая от начала участка теплообмена.

Рис. а – ламинарное течение; б – смешанное (переходное); в - турбулентное течение

Посмотрим как изменяется коэффициент теплоотдачи вдоль пластины.

Если вся пластина занята турбулентным слоем (в случае высокой стенки турбулентности набегающего потока, плохой обтекаемости пластины и т.п.), то коэффициент a изменяется в соответствии с кривой 1. при наличии на передней части пластины ламинарного пограничного слоя коэффициент a изменяется по более сложному закону. В этом случае теплоотдачу необходимо рассчитывать отдельно для участков с различными режимами течения.