Интегральная теорема Лапласа

 

Теорема 12.3 (Лаплас). Если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна p, а ненаступление события А – равна q=1-p, то вероятность того, что событие А в серии из n независимых испытаний появится от k₁ до k₂ раз приближенно равна значению определенного интеграла:

 

 

где ; , а – есть первообразная функции , т.е. которую называют интегральной функцией Лапласа.

 

Можно показать:

 

1) Эта функция нечетная, как первообразная от четной функции, т.е. Ф(-x)=-Ф(x), т.е. график Ф(x) симметричен относительно начала координат (0;0). Для функции Ф(x) также составлены таблицы значений. Данный интеграл не выражается через элементарные функции.

 

2) При возрастании x от 0 до Ф(x) быстро растет от 0 до 0,5, поэтому уже при x=5 считают, что Ф(5) 0,5 и для x>5 считают Ф(x)=0,5.

 

3) График интегральной функции Лапласа имеет вид (рис. 12.2).

 

Ф(х)

0,5

-0,5

Рис. 12.2

Замечание. Эта формула применяется при относительно больших n и значениях p, не очень близких к 0 или 1.

 

Пример 12.7. Вероятность поражения мишени при каждом выстреле равна 0,9. Какова вероятность того, что при 100 выстрелах будет не менее 95 поражений мишени?

 

 

 

Ответ. Вероятность поразить от 95 до 100 мишеней мала – 4,8%.

 

Пример 12.8. Найдем из условия предыдущей задачи №2 вероятность того, что будут вступать в силу от 40 до 45 решений суда.

 

Р₅₀(40;45)=Ф(0)+Ф(2,36)=0+0,49086 0,491;

 

n=50; k₁=40; k₂=45; p=0,9; q=0,1;

 

x₁= ;

 

x₂=

 

Ответ. Вероятность того, что вступят в силу от (40; 45) решений суда равна 49,1%.

 

Формула Пуассона. Когда p близко к 0 или 1, а значение n велико, формула Лапласа дает результаты, которые значительно отклоняются от результатов, полученных по формуле Бернулли. В случае, когда при возрастании n вероятность p появления интересующего нас события убывает, а n·p – постоянное число 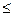10, то возникает ситуация, когда имеем дело с редко происходящими событиями. В таких ситуациях более точное значение, чем формула Лапласа, дает приближенная формула Пуассона.

 

Теорема 12.4 (Пуассон).Вероятность того, что при очень большом числе испытаний n, в каждом из которых вероятность p появления события А наступит ровно k раз вычисляется по формуле

 

где a=n·p; n – число произведенных испытаний; p – вероятность появления события А в каждом отдельном испытании, k – число испытаний, в котором событие А появилось; Р_n(k) – вероятность сложного события, состоящего в том, что при n испытаниях событие А появилось ровно k раз.

 

Эта формула является асимптотической формулой, т.е. это означает, что точность вычислений по формуле Пуассона тем выше, чем больше число испытаний n, как и формула Лапласа.

 

Теорема 12.5. Вероятность того, что при очень большом числе испытаний n, в каждом из которых вероятность p появления события А очень мала, что событие А наступит от k₁ до k₂ раз вычисляется по формуле

 

 

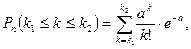
где Р_n(k₁;k₂) – вероятность сложного события, состоящего в том, что событие А произошло не менее k₁ раз и не более k₂ раз.

 

При вычислении Р_n(k) и Р_n(k₁;k₂) пользуются также таблицами, т.е. формулы Пуассона тоже затабулированы. В обеих формулах будем считать, что произведение n×p сохраняет постоянное значение, т.е. а=n×p, которое означает, что среднее число появлений события А при различных значениях n остается неизменным в различных сериях испытаний.

 

Пример 12.9. Среди 1000 человек приблизительно 8 левшей. Какова вероятность того, что среди сотни наугад выбранных людей не окажется ни одного левши?

 

n=100; k=0; p=0.008; a=n·p=0,8.

 

Р₁₀₀(0) .

Ответ: Вероятность того, что из группы 100 чел. не будет левшей равна 45%.

 

Пример 12.10. Вероятность того, что зерно пшеницы не прорастет принимается равным 0,005. Какова вероятность того, что из 800 посеянных семян не дадут всходов:

1) не более 10 семян? 2) более 10 семян?

 

1) k 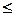10; n=800; a=800·0,005=4.

 

 

2) k>10 Р₈₀₀(k>10)=1-Р₈₀₀(k 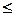10)=1-0,9972=0,0028.

 

Ответ: 1) Вероятность того, что из 800 семян не дадут всходов не более 10 семян равна 99,72% – практически достоверное событие; 2) прорастут более 10 семян с вероятностью 0,28% – практически невозможное событие.

 

Пример 12.11. Вероятность заболевания ящуром для каждой коровы равна 0,01. Какова вероятность того, что в стаде из 100 коров заболеют две?

 

p=0,01; n=100; a=n·p=100·0,01=1; k=2.

 

 

Ответ. Вероятность того, что в стаде из 100 коров заболеют 2 равна 18%.

 

Случайные величины

Понятие случайной величины. Для начала рассмотрим следующие примеры, приводящие к понятию случайной величины.

Пример 13.1. При наблюдении движения городского транспорта заметили, что число машин, проезжающих за 1 час через некоторый перекресток, под влиянием случайных обстоятельств принимает случайные значения.

 

Пример 13.2. Наблюдая стрельбу из одного и того же орудия при одном и том же прицеле, заметили, что расстояние места разрыва снаряда от орудия по неизвестным причинам принимает различные значения.

 

Пример 13.3. Учет числа писем, поступающих в некоторое почтовое отделение, показывает, что ежедневное количество писем принимает случайный характер.

 

Примеры 13.1 – 13.3 имеют общие черты:

 

· в них идет речь о величине, которая характеризует случайные события;

· каждая из этих величин может принимать соответствующие значения в зависимости от случайного исхода испытания.

 

При многократных повторениях опыта значения этих величин могут быть несколько отличны от предыдущих, так как на результаты измерений действуют различные причины, которые делятся на два вида:

· основные, которые определяют главное значение результата опыта;

· второстепенные, которые обуславливают расхождение значений.

 

При измерении каждой из этих величин можно утверждать, что значения их будут принадлежать некоторым ограниченным множествам, и могут принять любое значение из этого множества, а вот какое именно значение – это случайность (рис. 13.1).

 

Рис. 13.1

 

Определение 13.1. Случайной величиной называют переменную величину, значение которой зависит от случайного исхода некоторого испытания.

Другими словами, случайной величиной называется переменная величина, которая в результате испытания может принять то или иное числовое значение из множества возможных значений, причем заранее неизвестно, какое именно.

 

Случайные величины обозначают заглавным буквами латинского алфавита, а их возможные значения – малыми соответствующими буквам:

 

X: x₁; x₂;….; x_n; Y: y₁; y₂;…; y_n.

 

Пусть случайная величина X зависит от последовательности элементарных событий A ₁; A ₂;….; A_n, которые заданы на пространстве элементарных событий Е.

Это пространство можно рассматривать как область тех элементарных событий, которые обуславливают появление некоторого значения случайной величины Х.

 

Определение 13.2. Случайная величина Х есть функция на пространстве элементарных событий.

 

Значит, случайная величина связана со случайным событием, причем случайное событие – это качественная характеристика испытания. Независимым случайным событиям соответствуют независимые случайные величины.

 

Рассматривается два типа случайных величин: дискретные и непрерывные.

 

Определение 13.3. Случайная величина называется дискретной, если все ее возможные значения изолированы друг от друга и их можно занумеровать, т.е. величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности.

Определение 13.4. Случайная величина называется непрерывной, если все ее возможные значения заполняют некоторый конечной или бесконечный интервал, т.е. которая может принимать значения всех действительных чисел некоторого промежутка.

Вероятность того, что случайная величина Х примет значения х₁; х₂;….; x_n обозначают p₁; p₂;….; p_n, т.е.

 

P (X=x_i) = p_i;

P (X=x₁) = p₁; P (X=x ₂) = p ₂;… P (X=x _n) = p _n;

P (X=x) = p.

 

Определение 13.5. Законом распределения случайной величины называется соответствие, устанавливающее связь между возможными значениями случайной величины и их соответствующими вероятностями.