Определение 9.1. Генеральная совокупность без повторений – это набор некоторого конечного числа различных элементов а1; а2; …; аn-1; аn.
Примером генеральной совокупности может служить студенческая группа из n человек.
Определение 9.2. Выборкой объема m, где m £ n, называется произвольная группа из m элементов данной генеральной совокупности объема n.
Примером такой выборки является группа из m человек данной генеральной совокупности, изучающая английский или немецкий язык.
Каким минимальным признаком может отличаться одна выборка объема m от другой выборки такого же объема? Это их различие по крайней мере одним элементом или порядком расположения этих элементов.
Определение 9.3. Произведение натурального ряда чисел от 1 до n включительно называется факториалом числа n, т.е.
1·2·3·…·(n-1)·n=n!, причем принято считать 0!=1.
Определение 9.4. Размещениями без повторений из n элементов по m называются такие выборки, которые, имея по m элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, отличаются одна от другой либо составом элементов, либо порядком их расположения и обозначаются А  .
.
Выведем формулу вычисления числа размещений 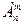 . Пусть имеем n элементов. Первый элемент можно выбрать n способами. Второй элемент будем выбирать из оставшихся (n-1) элементов, поэтому второй элемент можно выбрать (n-1)способами. Тогда пары двух элементов можно образовать n·(n-1) способами. Третий элемент придется отбирать из оставшихся (n-2) элементов. Это можно сделать (n-2) способами. Тогда тройки элементов можно образовать n·(n-1)·(n-2) способами и так далее. Размещения по m элементов можно образовать
. Пусть имеем n элементов. Первый элемент можно выбрать n способами. Второй элемент будем выбирать из оставшихся (n-1) элементов, поэтому второй элемент можно выбрать (n-1)способами. Тогда пары двух элементов можно образовать n·(n-1) способами. Третий элемент придется отбирать из оставшихся (n-2) элементов. Это можно сделать (n-2) способами. Тогда тройки элементов можно образовать n·(n-1)·(n-2) способами и так далее. Размещения по m элементов можно образовать
n·(n-1)·(n-2)·…·(n-(m-1))=n·(n-1)·(n-2)·…·(n-m+1) способами.
Значит
А  =n·(n-1)·(n-2)·…·(n-m+1) (1)
=n·(n-1)·(n-2)·…·(n-m+1) (1)
Если правую часть этого равенства умножим и разделим на произведение 1·2·3·(n-m-1)·(n-m), то получим равенство:
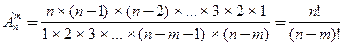 (2)
(2)
Это две формулы для вычисления числа размещений из n по m элементов в каждом, но вторая формула более удобна для запоминания.
В случае, когда m=n, одно размещение от другого отличается только порядком расположения элементов.
Определение 9.5. Перестановками без повторений из n элементов называются такие выборки из n элементов по n в каждой, которые содержат все n элементов и отличаются друг от друга только порядком расположения элементов и обозначаются 
Формула для вычисления числа перестановок из n элементов имеет вид
Рn=1·2·3·…·(n-2)·(n-1)·n=n!.
Определение 9.6. Сочетаниями без повторений из n элементов по m называются такие выборки, которые, имея по m элементов, выбранных из числа данных n элементов генеральной совокупности без повторений, отличающихся друг от друга хотя бы одним элементом, т.е. составом элементов, и обозначаются С  .
.
При m=n C  =1.
=1.
В каждом из С  сочетаний имеется m различных элементов, поэтому для каждого сочетания можно получить Рm перестановок. Совокупность всех выборок, полученных путем построения всех перестановок на базе каждого из С
сочетаний имеется m различных элементов, поэтому для каждого сочетания можно получить Рm перестановок. Совокупность всех выборок, полученных путем построения всех перестановок на базе каждого из С  сочетаний, представляет собой число размещений А
сочетаний, представляет собой число размещений А  , т.е.
, т.е.
С  ·Рm=А
·Рm=А  ,
,
откуда
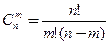
– это формула для вычисления числа сочетаний из n элементов по m элементов в каждом.
Одним из примеров размещений без повторений является совокупность трехзначных номеров, в каждом из которых нет повторения цифр.
Примером перестановок без повторений является совокупность всех десятизначных номеров, в каждом из которых нет повторения цифр.
Примером сочетаний без повторений являются всевозможные варианты состава делегации в количестве, например, трех человек от коллектива, в котором 10 человек.
Таким образом имеем (рис. 9.1):
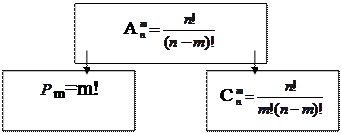 |
Рис. 9.1
Пример 9.1. Сколько разных стартовых шестерок можно образовать из числа 10 волейболистов?
Эти шестерки должны отличаться хотя бы одним игроком.
С  =
=  .
.
Можно составить 210 стартовых шестерок из команды в 10 человек.
Пример 9.2. Сколько разных пятизначных чисел можно составить из цифр 1;2;3;4;5 при условии, что ни одна цифра не повторяется?
Эти пятизначные числа должны отличаться только порядком расположения цифр.
Р5=5! = 1·2·3·4·5=120.
Из цифр 1;2;3;4;5 можно составить 120 пятизначных чисел.
Пример 9.3. В группе 30 человек. Необходимо направить трех человек на конференцию. Сколькими способами можно образовать такую тройку?
 .
.
Эти тройки делегатов должны отличаться хотя бы одним человеком. Тройку делегатов на конференцию можно образовать 4060 способами.
Алгебра событий
Вероятность объединения или сложения несовместных событий. Пусть n – общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий; m – число равновозможных элементарных событий благоприятствующих событию А; k – число равновозможных элементарных событий, благоприятствующих событию В.
|
|
|

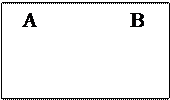


|
|
|
|
 ; Р(В)=
; Р(В)= 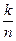 (рис. 10.1).
(рис. 10.1).
Рис. 10.1
По определению объединения (суммы) несовместных событий АUВ означает, что имеет место или А, или В. Но число благоприятствующих такому событию равно (m+k), поэтому (рис. 10.2):
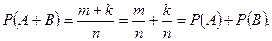
|
|
|





 Р(А+В) =
Р(А+В) =
Рис. 10.2
Эта теорема может быть распространена на любое конечное числособытий.
Следствие 10.1. Если события А;В;С образуют полную группу событий, то сумма их вероятностей равна единице.
(А+В+С) – достоверное событие 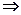
Р(А+В+С)=1 Þ Р(А)+Р(В)+Р(С)=1.
Следствие 10.2. Сумма вероятностей двух противоположных событий равна единице (рис. 10.3).
(А+  ) – полная группа событий Þ
) – полная группа событий Þ
Р(А+  )=Р(А)+Р(
)=Р(А)+Р( )=1 Þ Р(А)=1-Р(
)=1 Þ Р(А)=1-Р( );
);
|

|
 )=1-Р(А).
)=1-Р(А).
|
Рис. 10.3
Пример 10.1. В лотерее выпущено 10000 билетов и установлено: 10 выигрышей по 200р.; 100 – 100р.; 500 – 25р. и 1000 – по 5 рублей, остальные без выигрыша. Гражданин купил один билет. Какова вероятность того, что он выиграет не меньше 25р.? Обозначим события:
Событие А – выигрыш не менее 25руб.
Событие В – выигрыш равен 25руб.
Событие С – выигрыш равен 100руб.
Событие D – выигрыш равен 200руб.
Так как куплен только один билет, то А=В U С U D, где В;С;D события попарно несовместимые, поэтому
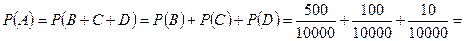
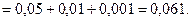
Ответ. Вероятность события А в данном случае невелика – 6,1%.
Пример 10.2. Бросают две монеты. Чему равна вероятность появления хотя бы одного герба? Обозначим события:
Событие А – появление герба при подбрасывании первой монеты.
Событие В – появление герба при подбрасывании второй монеты.
Событие С – появление хотя бы одного герба.
С=АUВ, но Р(С) 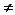 Р(А)+Р(В), т.к. события А и В совместимы. Но, если рассмотреть событие
Р(А)+Р(В), т.к. события А и В совместимы. Но, если рассмотреть событие  – выпадение герба не состоялось, то (
– выпадение герба не состоялось, то ( +С) – достоверное событие и Р(
+С) – достоверное событие и Р( )=
)=  , так как при подбрасывании двух монет могут произойти только события: ГГ (герб; герб); ЦЦ (цифра; цифра); ЦГ (цифра; герб); ГЦ (герб; цифра), поэтому Р(
, так как при подбрасывании двух монет могут произойти только события: ГГ (герб; герб); ЦЦ (цифра; цифра); ЦГ (цифра; герб); ГЦ (герб; цифра), поэтому Р( )+Р(С)=1 Þ Р(С)=1-Р(
)+Р(С)=1 Þ Р(С)=1-Р( )=1-
)=1-  =
= 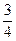 .
.
Вероятность суммы совместных событий. Пусть m – число равновозможных элементарных событий, благоприятствующих событию А; k – число равновозможных элементарных событий, благоприятствующих событию В. Пусть среди (m+k) элементарных событий содержится ℓ элементарных событий, благоприятствующих и событию А, и событию В, т.е. (А ∩ В).
Если n – общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий (рис. 10.4), то
 |
|
|
|



 Р(А)=
Р(А)=  ; Р(В)=
; Р(В)= 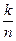 ;
;
|
|
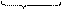
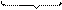
|
|
 .
.
Рис. 10.4
Теорема 10.2. Вероятность объединения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(A U B)=Р(A)+Р(B)-Р(A ∩ B).
Доказательство: (АUВ) – событие, состоящее в появлении или события А, или события В, или того и другого вместе (рис. 10.5):
Р(А UВ)= 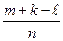 =
= 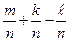 =P(А)+Р(В)-Р(А ∩ В)
=P(А)+Р(В)-Р(А ∩ В)
 |
|
 Р(А U В) =
Р(А U В) =
Рис. 10.5
что и требовалось доказать.
Пример 10.3. Подбрасываем две монеты. Какова вероятность выпадения хотя бы одного герба?
Событие А – выпадение герба при подбрасывании первой монеты.
Событие В – появление герба при подбрасывании второй монеты.
Р(A U B)=Р(A)+Р(B)-Р(A ∩ B)=  .
.
Определение 10.1. Вероятность события В при условии, что событие А произошло, называется условной вероятностью события В и обозначается Р(В/А); РА(В).
Определение 10.2. События А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет, т.е.
Р(В/А)=Р(В); Р(А/В)=Р(А);
РА(В)=Р(В); РВ(А)=Р(А).
Определение 10.3. События А и В называются зависимыми, если выполняются неравенства РВ(А) 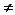 Р(А); РА(В)
Р(А); РА(В) 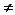 Р(В), т.е. вероятность одного события зависит от появления или не появления другого.
Р(В), т.е. вероятность одного события зависит от появления или не появления другого.
Теорема 10.3. ( Умножение зависимых событий). Вероятность пересечения двух зависимых событий А и В, т.е. вероятность совместного наступления А и В, равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло
Р(А ∩ В)=Р(А)·Р(В/А)=Р(В)·Р(А/В).
Доказательство: Пусть Е – пространство n элементарных событий (рис. 10.6).
Событию А – благоприятствует m элементарных событий.
Событию В – благоприятствует k элементарных событий.
Событию (А∩В) – благоприятствует ℓ элементарных событий.
Р(А ∩ В)=  ; Р(А)=
; Р(А)=  ; Р(В/А)=
; Р(В/А)=  .
.
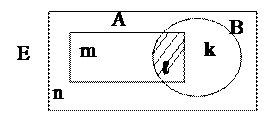
n
Рис. 10.6
Тогда

Р(A∩B)=Р(A)·Р(B/A).
Пример 10.4. В ящике 10 белых и 7 черных шаров. Последовательно вынимаем один за другим два шара. Какова вероятность того, что оба шара белые?
Событие А – первый вынутый шар белый.
Событие В – второй вынутый шар белый.
(А∩В) – оба вынутых шара белые.
Р(А∩В)=Р(А)·Р(В/А)= 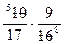 =
= 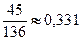 .
.
А и В – зависимые события.
Теорема 10.4 (Умножение независимых событий). Вероятность пересечения двух независимых событий равна произведению вероятностей этих событий:
Р(А ∩ В)=Р(А)·Р(В).
Пример 10.5. Бросают две игральные кости. Какова вероятность того, что на первой кости появится нечетное число очков и на второй пять очков?
Событие А – появление нечетного числа очков на первой кости: (1;3;5).
Событие В – появление 5 очков при бросании второй кости.
А и В – совместные и независимые события.
Р(А ∩ В)=Р(А)·Р(В)=  =
= 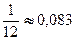 .
.






 (А∩В)
(А∩В)

