Формула Бернулли. В теории вероятностей любое случайное событие рассматривается как результат некоторого опыта. Если один и тот же опыт повторять неоднократно, то можно сказать, что проведено n повторных опытов или испытаний, в каждом из которых случайное событие А может появиться или не появиться.
Определение 12.1. Если вероятность появления случайного события А в каждом отдельном испытании не зависит от исхода других, то испытания называются независимыми.
В теории вероятностей, особенно при практическом ее применении, часто приходится решать задачи, связанные с повторными независимыми испытаниями. В подобных задачах нужно уметь определять вероятность: любого заданного числа k появления события А в результате серии n независимых повторных испытаний.
Определение 12.2. Серия из n независимых испытаний, в каждом из которых некоторое событие А имеет одну и ту же вероятность Р(А)=p, независимо от номера испытания, называется схемой Бернулли, или схемой повторных испытаний.
Якоб Бернулли (1654–1705) – швейцарский ученый, профессор Базельского университета. Дадим математическую формулировку задачи, возникающей в схеме Бернулли.
Пример 12.1. Проводится n независимых испытаний, в каждом из которых событие А может появиться или не появиться. Вероятность появления события А в каждом единичном испытании постоянна и равна p, а вероятность непоявления q=1-p. Найти вероятность того, что в этих n испытаниях событие А появится ровно k раз.
Ситуация, возникающая в схеме Бернулли, является весьма жизненной и потому исследование этой схемы в первую очередь привлекло внимание математиков, т.к. в последнее время повышено внимание к контролю качества выпускаемой продукции.
Теорема 12.1 (Бернулли). Вероятность сложного события, состоящего в том, что при n испытаниях, соответствующих схеме Бернулли, событие А, имеющее одну и ту же вероятность Р(А)=p для каждого отдельного испытания, появится ровно k раз, где 0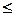 
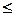k n, безразлично в какой последовательности, её можно вычислить по формуле
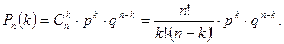
Доказательство. Элементарными исходами испытаний являются: событие Аi – появление события А в i испытании: i=1,2,…,n; событие 
i – непоявление события А в i-м испытании, где i=1,2,…,n. Значит Р(Аi)=p; Р( i)=1-p=q.
Пусть событие А имело место в первых k испытаниях и не произошло в (n-k) последующих, т.е. по определению произведения событий произошло сложное событие В:
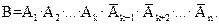
Так как испытания независимые, то применяя теорему умножения вероятностей, получим
.
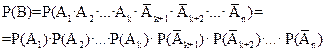Появления события А ровно k раз и события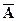 
ровно (n-k) раз с такой же вероятностью возможно и в любой другой последовательности. Число способов появления сложного события, состоящего в появлении событияименно k раз, инепоявлении (n-k) раз, равно числу всевозможных выборок из n элементов по k в каждой, отличающихся только составом элементов, т.е. С 
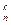. Применяя теорему сложения вероятностей несовместных событий, получим
Рn(k)= pk·qn-k+ pk·qn-k+…+ pk·qn-k = С 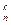pk·qn-k.
|
– это формула Бернулли.
Еще раз перечислим параметры, входящие в эту формулу: p – вероятность появления события А в каждом испытании; q – вероятность противоположного события ; n – число проведенных испытаний; k – число появлений события А, иногда называемое частотой события А, принимающее значения k=0,1,2,…,n.
Пример 12.2. Всхожесть семян некоторого сорта растений равна 80%. Для опыта отбирается 5 семян. Определить вероятность того, что из 5 посеянных семян прорастет 3 семени? не менее 3?
Будем считать высев 5 семян проведением пяти независимых испытаний. Для каждого из 5 посеянных семян вероятность прорасти постоянна Р(А)=0,8. Вероятность противоположного события Р()=1-Р(А)=0,2. Событие А – семя взошло; – семя не взошло. Надо найти Р5(3), т.е. вероятность того, что в 5 испытаниях событие А появится ровно 3 раза. Значит, n=5; p=0,8; q=0,2; k=3. По формуле Бернулли имеем:
Р5(3)=С 
·(0,8)3·(0,2)2=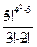 
·0,512·0,04=0,2048 
20,5%.
Р5(4)=С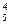 
(0,8)4·(0,2)= 
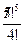·0,4096·0,2=0,4096.
Р5(5)=С 
·(0,8)5·(0,2)0=0,32768.
Р5(k 
3)=Р5(3)+ Р5(4)+ Р5(5)=0,02048+0,4096+0,32768=0,94208.
Ответ: 1) Вероятность того, что из 5 семян взойдет не менее трех семян, равна 94,2%. 2) Вероятность того, что из 5 посеянных семян прорастет ровно 3, равна 20,5%.
