Теорема 13.3. Математическое ожидание биноминальной величины 
равно произведению числа испытаний на вероятность появления события в каждом испытании
.
Доказательство. Случайная величина , распределенная по биноминальному закону, определяется числом появлении события 
при n испытаниях. Вероятность появления такого события в одном испытании равна p, непоявления – 
Пусть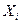 
– число появлений события при 
-ом испытании. Ясно, что 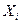может принять только два значения: 1 с вероятностью p(т.е. событие произошло)и0 с вероятностью q (т.е. не произошло)и, следовательно,
.
Однако 
, т.е. число появлений события в одной серии испытаний n можно рассматривать как сумму случайных величин.
Поэтому 
– числа появлений события в каждом испытании.
Теорема 13.4. Дисперсия биноминальной величины равна числу испытаний, умноженному на произведение вероятностей появления и непоявления события в каждом испытании
.
Случайная величина , распределенная по биноминальному закону, представляет число появлений события при n независимых испытаниях, когда вероятность появления события равна p, а непоявления – 
.
Пусть 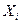- число появлений события при i -ом испытании, причем 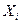может принять только два значения: 1 с вероятностью p, (т.е . произошло) и 0 с вероятностью q (т.е. не произошло). Тогда 
.
Находим 
Так как 
есть сумма независимых случайных величин, то
.
Пример 13.9. Вероятность выигрыша в каждой шахматной партии для некоторого игрока постоянна и равна 0,8. Составить ряд распределения вероятностей числа выигрышей игроком в пяти партиях, построить многоугольник распределения, найти числовые характеристики.
Случайная величина – число побед в пяти партиях является биноминальной величиной. По условию n= 5; p= 0,8; q= 0,2; X=0, 1, 2, 3, 4, 5. Рассчитаем вероятности по формуле Бернулли:
;
1. Составим ряд распределения:
 
| |||||||
| 0,0003 | 0,0064 | 0,0512 | 0,2048 | 0,4096 | 0,3277 |
2. Построим полигон распределения (рис. 13.5):
Рис. 13.5
3. Находим числовые характеристики
.
.
В среднем можно выиграть 4 партии. Вычисления 
и 
можно проверить по определению. Например:
= 0,0064 + 0,1024 + 0,6144 + 1,6389 + 1,6385 = 4,001.
Пример 13.10. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти 
– числа отказавших деталей, если испытанию на надёжность подлежат 10 деталей.
Биномиальная величина – число отказавших деталей. По условию n = 10; p = 0,2; q = 0,8. 
, значит в среднем за время испытаний из 10 деталей отказывают 2; 
.
Эту задачу можно было решить путем составления ряда распределения числа отказавших деталей и затем вычисления 
