Пусть стрелок производит выстрел по мишени. Как оценить вероятность попадания? Если события «попадания» и «промах» равновозможны, то ответ получаем сразу Р («попадание»)= 
. Но они могут быть и неравновозможны.
Пусть 1-й стрелок постоянно посещает тренировки по стрельбе и каждый раз из сотни выстрелов попадает в мишень 80 – 90 раз. Второй стрелок на стрельбище бывает редко, поэтому из сотни выстрелов попадает только 30–40 раз. Как оценить возможности попадания в цель каждым стрелком? Из практики.
| Произведено выстрелов, ℓ | ||||||||||
| Число попаданий 1-м стрелком, k1 | ||||||||||
| Число попаданий 2-м стрелком, k2 | ||||||||||
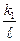
| 0,8 | 0,85 | 0,866 | 0,825 | 0,82 | 0,816 | 0,8 | 0,8125 | 0,8 | 0,81 |
| 0,3 | 0,25 | 0,266 | 0,3 | 0,3 | 0,316 | 0,314 | 0,3125 | 0,31 | 0,31 |
Эти отношения в какой-то мере зависят от числа произведенных выстрелов, т.е. отношение числа попаданий к числу произведенных выстрелов. Но видно, что это отношение для каждого стрелка колеблется около определенного числа: у 1 стрелка около 0,8; а у 2 стрелка около 0,3. Эти числа логично принять за оценку вероятности попадания. Эта оценка более надежна, чем больше проведено опытов с целью установления ее значения.
Определение 6.1. Статистической или относительной частотой события А называется отношение числа испытаний k, при которых событие А произошло, к числу ℓ испытаний, при проведении которых могло произойти или не произойти событие А, т.е. к общему числу испытаний и обозначается 
, т.е. индекс ℓ показывает зависимость статистической частоты от числа испытаний.
Практика показывает, что в случае, когда точно знаешь вероятность 
в классическом понимании, при достаточно большем числе испытаний ℓ, 
.
Определение 6.2. Вероятностью события 
называется то неизвестное число 
, около которого сосредотачиваются значения статистических частот наступления события при возрастании числа испытаний.
Это статистическое определение вероятности случайного события.
Свойства вероятности
1) Вероятность достоверного события равна 1; 
.
2) Вероятность невозможного события равна нулю; 
3) Вероятность любого события подчиняется неравенству; 
, т.к. 
, т.е.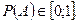 
Вывод. Вероятность – это мера на множестве событий.
Определение 7.1. Вероятностью случайного события А называется численная мера возможности наступления этого события при некотором испытании.
Элементы комбинаторики
Определение 8.1. Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.
Иногда комбинаторику рассматривают как введение в теорию вероятностей, так как методы комбинаторики очень помогают в теории вероятностей осуществить подсчет числа возможных исходов и числа благоприятствующих исходов в разных конкретных случаях. В теории вероятностей принято говорить не о комбинациях, а о “выборках”. Поэтому мы будем говорить о “выборках”. В комбинаторике рассматриваются виды выборок – перестановки, размещения, сочетания.
