Человека окружает мир событий. Он часто замечает такой факт: одни события при реализации данного комплекса условий непременно происходят, другие же могут произойти, а могут и не произойти. Рассмотрим группу таких событий.
| Событие | Реализация комплекса условий | Исход |
| А1 | При нагревании проволоки | Ее длина увеличилась |
| А2 | При бросании игральной кости | Выпали 4 очка |
| А3 | При бросании монеты | Выпал герб |
| А4 | При осмотре почтового ящика | Найдены три письма |
| А5 | При низкой температуре | Вода превратилась в лед |
Про события А1 и А5 мы вынуждены сказать, что они произойдут закономерно, а про А2; А3; А4 – что они могли произойти, но могло быть и иначе, т.е. мы ощущаем случайность событий А2; А3; А4. Значит, событие – это исход наблюдения или эксперимента, когда оно при реализации данного комплекса условий может произойти, а может и не произойти, есть случайное событие.
Определение 2.1. Испытание, эксперимент, наблюдение или опыт – это осуществление определенного комплекса условий, при которых производится испытание.
Определение 2.2. Случайным событием называется такой исход наблюдения или эксперимента, который при реализации данного комплекса условий может произойти, а может и не произойти, т.е. это качественный результат эксперимента или экспериментов, если они повторяются многократно.
Обозначаются события заглавными буквами латинского алфавита: А; В; С; D;….
Представим себе, что некоторый прямоугольник Е мы разрезали на n прямоугольных пронумерованных карточек ℓi (i=1;…;n).
| ℓ5 | ℓ7 | |||||||||
| ℓi | |||||||||
| ℓ1 | ℓn |
Испытание S будет состоять в том, что после хорошей перетасовки одну карточку наугад вытаскиваем из всей стопки.
При такой операции:
1) одно из событий “вытащена одна карточка” непременно произойдет;
2) при одном испытании вытаскивание одной из карточек проявляется в одном и только в одном исходе, т.е. если была вытащена карточка №17, т.е. произошло событие ℓ17, то в это же время не может произойти событие ℓ5, состоящее в вытаскивании карточки №5.
Событие ℓi, состоящее в появлении карточки с номером i = 1,2,…, n, служит примером элементарных событий, а прямоугольник Е – пространством элементарных событий, связанных с реализацией испытания S – вытаскиванием случайной карточки после тщательной перетасовки.
Пусть теперь пространство элементарных событий Е, определенное бросанием игральной кости, представляет событие, где ℓi выпало i очков =1,2;…;6.
 | |||
| |||
 ℓ1 ℓ1
|   ℓ2 ℓ2
|  ℓ3 ℓ3
|  ℓ4 ℓ4
|  ℓ5 ℓ5
|  ℓ6 ℓ6
|
 |  | ||
Рассмотрим события:
1) А – выпало четное число очков;
2) В – выпало не меньше двух очков;
3) С – выпало не больше двух очков.
Событие А произошло, если произошло одно из элементарных событий: ℓ2; ℓ4; ℓ6, которые ему благоприятствуют.
Событие В произошло, если произошли элементарные события: ℓ2; ℓ3; ℓ4; ℓ5;ℓ6, благоприятствующие ему.
Событие С произошло, если произошли ℓ1; ℓ2, благоприятствующие ему.
Определение 2.3. Возможные, исключающие друг друга, результаты одного испытания называются элементарными событиями.
Определение 2.4. Элементарные события, которые благоприятствуют появлению события А, называются благоприятствующими событию А.
Значит, событие А можно рассматривать как подпространство ему благоприятствующих элементарных событий (ℓ2; ℓ4; ℓ6).
Событие В – как подпространство ему благоприятствующих элементарных событий (ℓ2; ℓ3; ℓ4; ℓ5;ℓ6).
Событие С – как подпространство ему благоприятствующих элементарных событий (ℓ1; ℓ2).
Виды событий
Рассмотрим пример. На трех карточках проставлены цифры 1; 2; 3. После перетасовки карточек по очереди выстраиваем их в один ряд. Получается трехзначное число ℒ. Пространство элементарных событий Е представляет собой событие ℓi, где i = 1; 2; …; 6.
|
| ℓ1 ℒ=123 | ℓ2 ℒ=213 | ℓ3 ℒ=312 | ℓ4 ℒ=231 | ℓ5 ℒ=132 | ℓ6 ℒ=321 |
На этом пространстве Е рассмотрим события: А – получилось число ℒ < 123;
В – получилось число ℒ ³123.
Испытание S – после перетасовки карточки выстраиваем в один ряд.
Определение 3.1. Если среди элементарных событий пространства Е, определяемого испытанием S, нет ни одного элементарного события, благоприятствующего событию А, то оно называется невозможным по отношению к испытанию S.
Определение 3.2. Если все элементарные события пространства Е, определяемого испытанием S, благоприятствуют событию В, то событие В называется достоверным по отношению к испытанию S.
Иначе говоря: событие, которое в результате испытания является единственно возможным его исходом, называется достоверным. Если при испытании событие заведомо произойти не может, то оно называется невозможным.
Пример 3.1. Достоверные события: А – выплата рубля шестью монетами;
В – наугад выбранное трехзначное число не больше 1000.
Невозможные события: С – выплата 10 рублей четырьмя купюрами.
В нашем примере:
Событие А – получилось число ℒ<123 – это невозможное событие.
Событие В – получилось число ℒ≥ 123 – это достоверное событие.
Операции над событиями
Между событиями соблюдаются отношения, аналогичные отношениям “больше”, “меньше” или “равно”, как и между числами.
Объединение (U)
A
| ℓ1 | ℓ2 | ℓ3 | |||||||||
| ℓ4 | ℓ6 | ℓ7 | ℓ9 |
| ||||||
| ℓ5 | ℓ8 | ℓ11 | ℓ12 |
B
Пусть событию А благоприятствуют элементарные события ℓ1; ℓ2;…; ℓ7, а событию В – элементарные события ℓ8; ℓ9;…; ℓ12. Пусть событию С = АUВ благоприятствуют элементарные события ℓ1; ℓ2;…; ℓ11; ℓ12.
Событие С называют объединением событий А и В, это означает, что произошло или А, или В.
A
| ℓ1 | ℓ2 | ℓ3 | |||||||
| ℓ5 | ℓ6 | ℓ7 | ||||||
| ℓ8 | ℓ9 | ℓ10 | |||||||
| |||||||||
Событию А→благоприятствуют элементарные события ℓ1; ℓ2;…; ℓ6; ℓ7.
Событию В→ℓ6; ℓ7; ℓ8; ℓ9;ℓ10.
С= АUВ → элементарные события ℓ1; ℓ2; …ℓ10.
События ℓ6; ℓ7  и А и В.
и А и В.
Значит событие С означает, что произошло или А; или В; или и то и другое вместе.
Определение 4.1. Объединением событий А и В называется событие С, состоящее в наступлении по крайней мере одного из событий А и В.
Определение 4.2. Объединением событий А1; А2;…; Аn называется событие А, состоящие в появлении хотя бы одного из событий А1; А2;…; Аn, т.е. или А1; или А2; …; или Аn, или несколько из них, или всех.
Пример 4.1. Куплен лотерейный билет – испытание S.
Событие А – выигрыш 10руб.
Событие В – выигрыш 20руб.
Событие С – выигрыш 30руб.
Событие D – выигрыш 40руб.
Событие К = АUВUСUD – выигрыш не более 40руб.
Пересечение (∩)
Пусть событию А благоприятствуют элементарные события ℓ1; ℓ2; …;ℓ7, а событию В- ℓ6; ℓ7;…; ℓ10. Пусть событию С благоприятствуют элементарные события, заштрихованные дважды, т.е. ℓ6; ℓ7, значили произошло и событие А, и событие В.
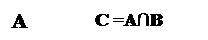 |
| ℓ2 | ℓ3 | ℓ4 | ℓ5 | ℓ6 | ℓ7 | ||||
| ℓ9 | ℓ10 | ||||||||
Определение 4.3. Пересечением двух событий А и В называется событие С, состоящее в одновременном появлении и события А, и события В, и обозначается С=А∩В.
Определение 4.4. Пересечением событий А1; А2; А3; …; Аn называется событие А, состоящее в одновременном появлении всех (и А1; и А2; …; и Аn) событий А1; А2; …; Аn.
А= А1∩А2∩…∩Аn.
Пример 4.2. Испытание – в подъезд входит человек.
Событие А – входящий в подъезд человек – мужчина.
Событие В – входящий в подъезд человек – светловолосый.
Событие С – входящий в подъезд человек – светловолосый мужчина.
Событие С происходит только при одновременном исполнении событий А и В, поэтому С =А∩В.
Пример 4.3. Испытание S – произвольно выбираем два двузначных числа.
Событие А – выбранные числа кратные 2.
Событие В – выбранные числа кратные 3.
Событие С – выбранные числа кратные 6.
С=А ∩ В. Событие С происходит, если одновременно происходят события А и В. Если одно из событий А или В не произойдет, то не произойдет и событие С.
Пусть событию А благоприятствуют элементарные события ℓ1; ℓ2; ℓ3; ℓ4, а событию В – ℓ5; ℓ6; ℓ7 в результате испытания S.
|
| ℓ1 | ℓ2 | |||||
| ℓ3 | ℓ4 | |||||
| ℓ5 | ℓ6 | ||||
| ℓ7 | |||||
|
Ясно видно, что совместное осуществление А и В невозможно: элементарных событий, благоприятствующих и тому, и другому событию, нет. А∩В=Æ – невозможное событие.
Определение 4.5. Два события А и В, пересечение которых – невозможное событие, называются несовместными событиями.
Определение 4.6. Два события в результате одного испытания называются несовместными, если появление одного из них исключает появление другого.
Определение 4.7. Объединением двух несовместных событий А и В называется событие С, осуществляющееся в появлении либо события А1, либо события В.
Определение 4.8. Два события А и В называются совместимыми, когда существует по крайней мере одно элементарное событие, благоприятствующее и событию А, и событию В.
Определение 4.9. Два события называются совместными, если в результате одного испытания появление одного события не исключает появление другого.
Рассмотрим пары событий:
А1 – выпадение герба при подбрасывании монеты;
А2 – не выпадение герба при подбрасывании монеты;
В1 – выздоровление больного;
В2 – не выздоровление больного;
С1 – появление новой кометы в текущем году;
С2 – не появление новой кометы в текущем году.
Естественно, события в каждой из пар считать противоположными.
Любая из пар событий удовлетворяет следующим двум свойствам:
1. Объединение каждой пары событий – есть достоверное событие: А1 UА2; В1UВ2; С1 U С2.
2. Пересечение событий каждой пары – есть невозможное событие: А1 ∩ А2; В1∩ В2; С1 ∩ С2.
Тогда введем определение.
Определение 4.10. Если объединение событий А и В – достоверное событие, а пересечение – невозможное событие, то события А и В называются противоположными, т.е. А=  или B=
или B=  .
.
Значит, что события А и  , т.е. противоположные события образуют полную группу событий.
, т.е. противоположные события образуют полную группу событий.  дополняет событие А в отношении всего пространства элементарных событий Е (рис. 5.1)
дополняет событие А в отношении всего пространства элементарных событий Е (рис. 5.1)
|
| ||||||||
| ||||||||







