Составить уравнение плоскости, которая проходит через точку М1(2; 1; -1) и имеет нормальный вектор n={1; -2; 3}.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор n={5; 0; -3}. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Точка Р(2; -1; -1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Даны точки M1(3; -1; 2), M2(4; -2; -1). Составить уравнение плоскости, проходящей через точку М1 перпендикулярно вектору  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, проходящей через точку М1(3; 4; -5)
параллельно векторам a1={3; 1; -1) и a2={1; -2; 1}.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что уравнение плоскости, проходящей через точку М0(x0, y0, z0) параллельно векторам a1={l1, m1, n1} и a2={l2; m2; n2}, может быть представлено в следующем виде:
 . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, проходящей через точки M1(2; -1; 3), M2(3; 1; 2) параллельно вектору a={3; -1; 4}.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что уравнение плоскости, проходящей через точки M1(x1; y1; z1), M2(x2, y2, z2) параллельно вектору a={l; m; n}, может быть представлено в следующем виде:
 . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, проходящей через точки М1(3; -1; 2), М2(4; -1; -1), М3(2; 0; 2).

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что уравнение плоскости, проходящей через точки M1(x1; y1; z1), M2(x2, y2, z2), M3(x3; y3; z3), может быть представлено в следующем виде:
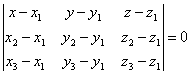 . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.1 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.2 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.3 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.4 | 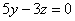 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.5 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 923.6 |  . .

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Установить, какие из следующих пар уравнений определяют параллельные плоскости: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 924.1 | 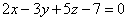 , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 924.2 |  , , 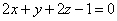 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 924.3 |  , ,  . .

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 925.1 |  , , 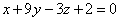 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 925.2 |  , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 925.3 |  , ,  . .

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить, при каких значениях l и m следующие пары уравнений будут определять параллельные плоскости: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 926.1 |  , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 926.2 |  , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 926.3 |  , ,  . .
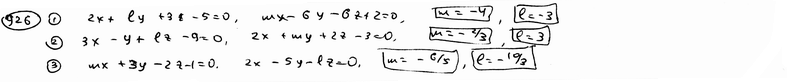
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить, при каких значениях l и m следующие пары уравнений будут определять перпендикулярные плоскости: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 927.1 |  , , 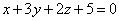 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 927.2 | 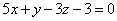 , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 927.3 |  , ,  . .
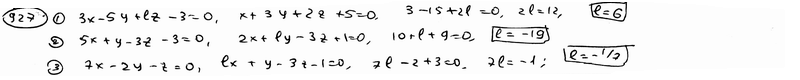
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить двугранные углы, образованные пересечением следующих пар плоскостей: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 928.1 |  , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 928.2 |  , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 928.3 | 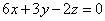 , ,  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 928.4 |  , ,  . .

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, которая проходит через точку М1(3; -2; -7) параллельно плоскости  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям  , ,  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, которая проходит через точку М1(2; -1; 1) перпендикулярно к двум плоскостям  , ,  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что уравнение плоскости, проходящей через точку М0(x0; y0; z0) перпендикулярно к плоскостям  , ,  , может быть представлено в следующем виде: , может быть представлено в следующем виде:
 . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Составить уравнение плоскости, которая проходит через две точки М1(1; -1; -2), M2(3; 1; 1) перпендикулярно к плоскости  . .
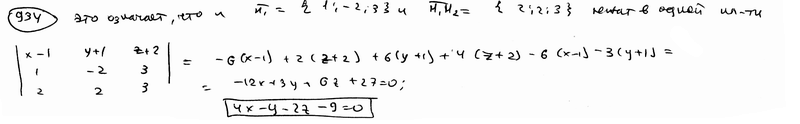
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что уравнение плоскости, проходящей через две точки M1(x1; y1; z1), M2(x2, y2, z2) перпендикулярно к плоскости 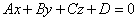 , может быть представлено в следующем виде: , может быть представлено в следующем виде:
 . .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Установить, что три плоскости  , ,  , ,  имеют общую точку, и вычислить ее координаты. имеют общую точку, и вычислить ее координаты.
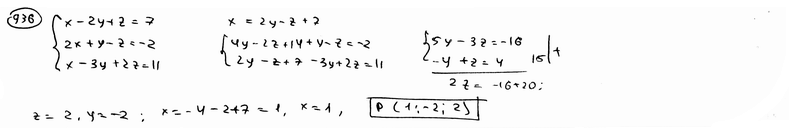
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что три плоскости  , ,  , ,  проходят через одну прямую. проходят через одну прямую.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказать, что три плоскости  , ,  , ,  пересекаются по трем различным параллельным прямым. пересекаются по трем различным параллельным прямым.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определить, при каких значениях a и b плоскости  , ,  , ,  : :
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 939.1 | имеют одну общую точку; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 939.2 | проходят через одну прямую; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 939.3 | пересекаются по трем различным параллельным прямым.
 Глава 39. Неполные уравнения плоскостей.
Уравнения плоскости "в отрезках"
Глава 39. Неполные уравнения плоскостей.
Уравнения плоскости "в отрезках"
|

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 6593 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:



 с координатными осями.
с координатными осями.

 . Написать для нее уравнение в отрезках.
. Написать для нее уравнение в отрезках.

 на координатных осях.
на координатных осях.

 от координатного угла Оху.
от координатного угла Оху.
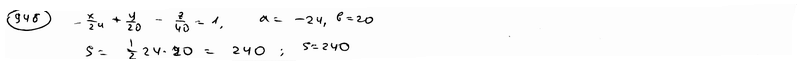
 и координатными плоскостями.
и координатными плоскостями.

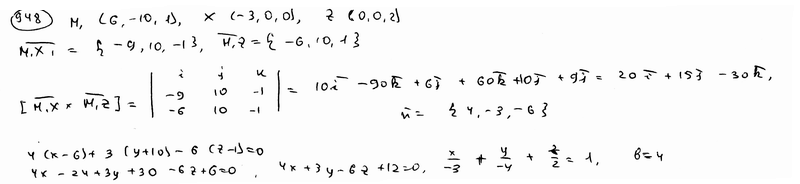


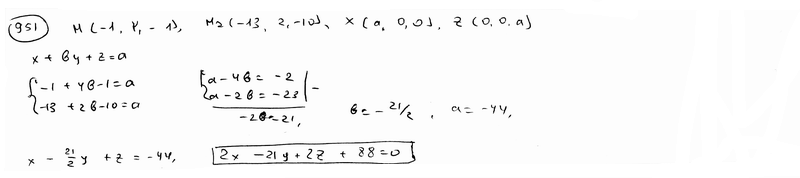



 и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3.
и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3.


