Даны точки М1(2; -3; 6), M2(0; 7; 0), M3(3; 2; -4), M4( ; 4; -5), M5(1; -4; -4), M6(2; 6; ; 4; -5), M5(1; -4; -4), M6(2; 6;  ). Установить, какие из них лежат на поверхности, определенной уравнением ). Установить, какие из них лежат на поверхности, определенной уравнением 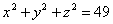 , и какие не лежат на ней? Какая поверхность определена данным уравнением? , и какие не лежат на ней? Какая поверхность определена данным уравнением?

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На поверхности 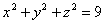 найти точку, для которой: 1). Абсцисса равна, ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4. найти точку, для которой: 1). Абсцисса равна, ордината рана 2; 2). Абсцисса равна 2, ордината равна 5, 3). Абсцисса равна 2, апликата равна 2; 4). Ордината равна 2, апликата равна 4.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Установить, какие геометрические образы определяются следующими уравениями в декартовых прямоугольных координатах пространства: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.1 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.2 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.3 | 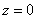 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.4 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.5 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.6 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.7 | 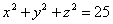 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.8 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.9 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.10 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.11 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.12 | 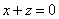 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.13 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.14 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.15 | 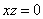 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.16 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.17 | 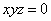 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.18 |  ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.19 | 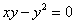 ; ;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 887.20 |  . .

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Даны две точки F1(-c; 0; 0) и F2(c; 0; 0). Вывести уравнение геометрического места точек, сумма расстояний от которых до двух данных точек есть величина постоянная, равная 2а при условии a>0, c>0; a>c.
Задача 0888
Даны две точки F1(—с; 0; 0) и F2(c; 0; 0). Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек есть величина постоянная, равная 2а при условии а>0, с>0; а>с..
Р е ш е н и е. Обозначим буквой М произвольную точку пространства, буквами х, у, z — её координаты. Так как точка М может занимать любое положение, то х, у и z являются переменными величинами; их называют текущими координатами.
Точка М лежит на данной поверхности в том и только в том случае, когда
MF1 + MF2 = 2a (1)
Это есть определение поверхности, выраженное символически. Выразим MF1 и MF2 — через текущие координаты точки М:
MF1 =  , MF2 =. , MF2 =.  Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение
Подставим полученные выражения в равенство (1). Тем самым мы найдём уравнение
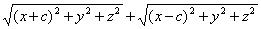 (2)
которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности.
Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде.
Уединим в уравнении (2) первый радикал: (2)
которое связывает текущие координаты х, у, z. Это и есть уравнение данной поверхности.
Действительно, для каждой точки М, лежащей на данной поверхности, выполняется условие (1) и, следовательно, координаты такой точки будут удовлетворять уравнению (2); для каждой точки, не лежащей на поверхности, условие (1) не будет выполняться и, следовательно, её координаты не будут удовлетворять уравнению (2). Таким образом, задача решена; дальнейшие выкладки имеют целью представить уравнение поверхности в более простом виде.
Уединим в уравнении (2) первый радикал: 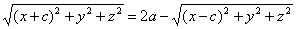 возведём обе части этого равенства в квадрат и раскроем скобки; мы получим:
x2 + 2cx+с2+y2 + z2 =4а2 — 4а возведём обе части этого равенства в квадрат и раскроем скобки; мы получим:
x2 + 2cx+с2+y2 + z2 =4а2 — 4а 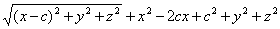 или а
или а  Снова, освобождаясь от радикала, найдём:
a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2,
или
(а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3)
Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид
b2x2 + а2y + a2z2 = a2b2
или
Снова, освобождаясь от радикала, найдём:
a2x2 — 2a2cx + а2с2 + a2 y2 + a2 z2 = a4 — 2а2сх + с2x2,
или
(а2 — с2) х2 + a2y2 + a222 = а2 (а2 — с2). (3)
Так как а > с, то а2 — с2 > 0; положительное число a2 — с2 обозначим через b2. Тогда уравнение (3) примет вид
b2x2 + а2y + a2z2 = a2b2
или  Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида.
Рассматриваемая поверхность называется эллипсоидом вращения. Уравнение (4) называется каноническим уравнением этого эллипсоида.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение сферы, центр которой находится в начале координат и радиус которой равен r.
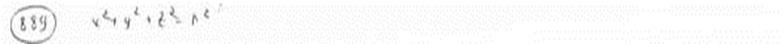
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение сферы, центр которой C( , ,  , ,  ) и радиус которой равен r. ) и радиус которой равен r.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Из точки P(2; 6; -5) проведены всевозможные лучи до пересечения с плоскостью Oxz. Составить уравнение геометрического места их середин.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Из точки А(3; -5; 7) проведены всевозможные лучи до пересечения с плоскостью Oxy. Составить уравнение геометрического места их середин.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Из точки С(-3; -5; 9) проведены всевозможные лучи до пересечения с плоскостью Oyz. Составить уравнение геометрического места их середин.

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение геометрического места точек, разность квадратов расстояний от которых до точек F1(2; 3; -5), F2(2; -7; -5) есть величина постоянная, равная 13.
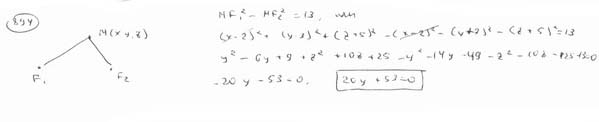
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение геометрического места точек, сумма квадратов расстояний от которых до двух точек F1(-a; 0; 0), F2(a; 0; 0) равна постоянной величине  . .
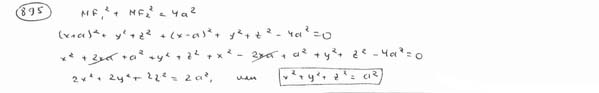
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вершины куба суть точки A(-a; -a; -a), B(a; -a; -a), C(-a; a; -a), D(a; a; a). Составить уравнение геометрического места точек, сумма квадратов расстояний от которых до граней этого куба есть величина постоянная, равная  . .

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение геометрического места точек, равноудаленных от двух точек M1(1; 2; -3), M2(3; 2; 1).

| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение геометрического места точек, сумма расстояний от которых до двух даных точек F1(0; 0; -4), F2(0; 0; 4) есть величина постоянная, равная 10.
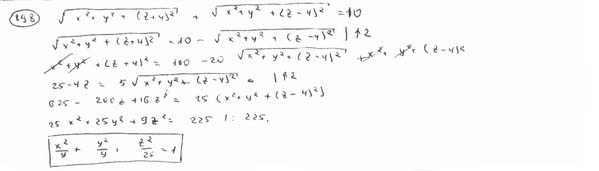
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вывести уравнение геометрического места точек, разность расстояний от которых до двух данных точек F1(0; -5; 0), F2(0; 5; 0) есть величина постоянная, равная 6.
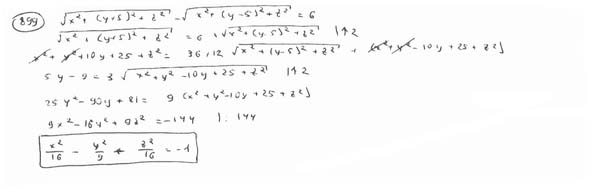 Глава 36. Уравнения линии. Задача о пересечении трех поверхностей
Глава 36. Уравнения линии. Задача о пересечении трех поверхностей
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 35. Уравнение поверхности
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 1191 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:
 ,
,  и какие не лежат на ней.
и какие не лежат на ней.

 ,
,  ,
,  ;
;
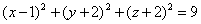 ,
,  .
.

 найти точку:
найти точку:

 ,
,  ;
;
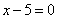 ,
,  ;
;
 ;
;
 ,
,  .
.



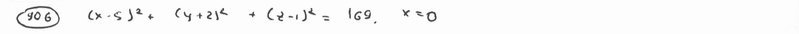

 .
.

 ,
,  .
.


