Рассмотрим движение электрона под действием внешнего электрического поля. В этом случае на электрон действует сила F, пропорциональная напряженности поля ЕЭ
F = – eЕЭ. (4.8)
Для свободного электрона эта сила является единственной, и основное уравнение динамики будет иметь вид
, (4.9)
где Jr – групповая скорость, т.е. скорость электрона.
Энергия электрона, как мы помним, определяется выражением
. (4.10)
Если электрон движется в кристалле, то на него также действуют силы потенциального поля узлов решетки Екр и уравнение (4.9) примет вид
. (4.11)
Несмотря на внешнюю простоту, уравнение (4.11) в общем виде не решается вследствие сложности и неоднозначности Екр. Обычно применяют метод эффективной массы для описания движения электрона в поле кристалла. В этом случае уравнение (4.11) записывают в виде
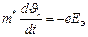, (4.12)
где m * – эффективная масса электрона.
Иными словами, эффективная масса электрона учитывает влияние потенциального поля кристалла на этот электрон. Выражение (4.10) принимает вид
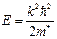, (4.13)
такой же, как и для энергии свободного электрона.
Рассмотрим свойства эффективной массы. Для этого вспомним выражение, определяющее групповую скорость Jr =d E /d k, и подставим его в формулу для ускорения а
. (4.14)
Если учесть, что dk / dt = Е / ħ, то можно записать выражение для эффективной массы
. (4.15)
Последнее выражение, впрочем, можно получить двукратным дифференцированием (4.13) по k. Подставляя (4.10) в (4.15), можно убедиться, что для свободного электрона m *= m.
Для электрона, находящегося в периодическом поле кристалла, энергия уже не является квадратичной функцией k, и поэтому эффективная масса электрона в общем случае является сложной функцией от k. Однако вблизи дна или потолка зоны, где выполняется квадратичная зависимость, эффективная масса перестает зависеть от k и становится постоянной. Если энергию электрона отсчитывать от экстремальной энергии, то можно записать для дна зоны выражение
E (k)= E min+ Ak 2, (4.16)
для потолка зоны, соответственно
E (k)= E max– Bk 2, (4.17)
где A и B – коэффициенты пропорциональности.
Подставив (4.10) в выражение для эффективной массы (4.15), найдем ее значение вблизи дна зоны
m *= ħ 2/2 A. (4.18)
Поскольку ħ и A – величины положительные и постоянные, то и эффективная масса электрона вблизи дна зоны тоже постоянна и положительна, т.е. ускорение электрона происходит в направлении действующей силы. Однако сама величина эффективной массы может быть и больше, и меньше массы покоя электрона (прил. 2). Эффективная масса электрона существенно зависит от ширины энергетической зоны, где он находится. С увеличением энергии растут ширина запрещенной зоны и скорость перемещения электрона. Так, электроны широкой валентной зоны 3s имеют эффективную массу, практически равную массе покоя электрона. Напротив, электроны узкой зоны 1s имеют ничтожную скорость перемещения и эффективную массу, на много порядков превышающую массу покоя электрона.
Еще более необычно поведение эффективной массы вблизи потолка зоны. Подставив выражение (4.17) в (4.15), получим соотношение
m *=– ħ 2/2 B. (4.19)
Из полученного выражения следует, что эффективная масса электрона вблизи потолка зоны является величиной постоянной и отрицательной. Такой электрон ускоряется против направления действующей силы. Абсолютная величина эффективной массы также может сильно отличаться от массы покоя электрона.
Такое поведение эффективной массы объясняется тем, что движение электрона в кристалле происходит под действием не только силы внешнего электрического поля, но и под действием потенциального поля кристалла.
Если под действием ускоряющего поля происходит уменьшение взаимодействия электрона с решеткой, это вызывает увеличение кинетической энергии, т.е. скорости электрона. Внешне такое ускорение выглядит, как уменьшение массы электрона.
Возрастание эффективной массы электрона сверх массы покоя имеет причиной обратимый процесс перехода части энергии внешнего поля в потенциальную энергию взаимодействия электрона с решеткой. В этом случае его кинетическая энергия возрастает незначительно. Внешне это выглядит, как возрастание массы электрона.
Наконец, в кристалле возможна и такая ситуация, когда в потенциальную энергию взаимодействия переходит не только вся работа внешней силы, но и часть кинетической энергии. В этом случае под действием внешней силы скорость электрона будет не возрастать, а убывать. Отрицательному ускорению должна соответствовать и отрицательная масса электрона.
В завершение необходимо подчеркнуть, что эффективная масса не описывает инертных или гравитационных свойств электрона, но является удобным способом учитывать взаимодействие электрона и потенциального поля кристаллической решетки.
