Функция распределения для вырожденного коллектива фермионов впервые была получена итальянским физиком Энрико Ферми и английским физиком Полем Дираком:
 . (3.20)
. (3.20)
Химический потенциал μ для фермионов обычно называют энергией, или уровнем Ферми – ЕФ.
Анализ выражения показывает, что при Е = ЕФ и температуре Т >0, fФ (Е)=½, т.е. вероятность заселения уровня Ферми при Т >0 равна ½.
Для того чтобы понять свойства функции Ферми-Дирака, полезно рассмотреть ее поведение при Т =0. Проводник можно представить в виде потенциальной ямы для электронов, выход из которой требует совершения работы по преодолению сил связи, удерживающих электроны – работы выхода (рис. 3.3, а). На рисунке показаны энергетические уровни, которые могут занимать электроны. Согласно постулату Паули, на каждом уровне может располагаться не более двух электронов (с противоположными спинами).

а) б)
Рис. 3.3. Электроны в проводнике: а – Т =0; б – Т >0
Как видно на рисунке, при Т =0 все уровни ниже уровня Ферми заняты, а все уровни выше этого уровня пусты, т.е. функция fФ (Е) при Т =0 имеет форму ступеньки (рис. 3.4, а).

а) б)
Рис. 3.4. Распределение Ферми-Дирака: а – функция распределения Ф-Д;
б – полная функция распределения
Таким образом можно определить физический смысл уровня Ферми, но только для проводников. В случае полупроводников или изоляторов это определение неприемлемо, поскольку в этих материалах недостаточно свободных электронов и уровень Ферми находится в запрещенной зоне (п. 4.5).
Умножив функцию распределения (3.20) на число состояний (3.13), получим выражение для полной функции распределения при Т =0 (рис. 3.4, б)
 , (3.21)
, (3.21)
поскольку в интервале ЕФ ≥ Е >0, fФ (Е)=1.
Проинтегрировав (3.21) в указанном интервале энергий, будем иметь выражение для энергии Ферми:
 , (3.22)
, (3.22)
где n – концентрация электронного газа в проводнике.
Используя выражение (3.21), можно получить формулы для вычисления средней энергии –  и максимальной скорости электронов при абсолютном нуле
и максимальной скорости электронов при абсолютном нуле
 , (3.23)
, (3.23)
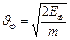 . (3.24)
. (3.24)
Необходимо отметить, что кинетическая энергия электронов ЕФ не является тепловой энергией, а имеет чисто квантовую природу и определяется свойствами электронов как Ферми-частиц.
С повышением температуры электроны подвергаются тепловому возбуждению и переходят на более высокие энергетические уровни (см. рис. 3.3, б). Происходит “размывание” функций распределения (см.
рис. 3.4), и ступенька Е = ЕФ преобразуется в интервал, ширина которого равна 2 kT. Однако более глубокие состояния электронов остаются неизменными.
Проведенные расчеты показывают, что число термически возбужденных частиц составляет для комнатной температуры всего 1...2% от общего числа. Если проинтегрировать полную функцию распределения во всем энергетическом диапазоне, то можно получить выражение для температурной зависимости энергии Ферми
 , (3.25)
, (3.25)
где ЕФ о – энергия Ферми для Т =0К (3.22).
Напомним, что тепловое возбуждение так незначительно влияет на характеристики вырожденного Ферми-газа, что во многих случаях этим влиянием можно пренебречь и считать ЕФ = ЕФ о во всем температурном диапазоне.
Можно также вычислить среднюю энергию электронов  при ненулевой температуре Т >0
при ненулевой температуре Т >0
 , (3.26)
, (3.26)
где Еп – полная энергия электронного газа.
Ранее мы говорили о Ферми-газе, считая его вырожденным коллективом. Однако, в случае выполнения критерия (3.11) G >> N, можно говорить о снятии вырождения. Тогда критерий невырожденности (3.11) примет вид
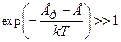 (3.27)
(3.27)
или в случае Е =0
 . (3.28)
. (3.28)
Из последнего соотношения следует, что для невырожденного Ферми-газа должно выполняться условие
- ЕФ > kT (3.29)
При выполнении условия (3.27) единицей в знаменателе выражения (3.20) можно пренебречь, и выражение (3.20) совпадает с формулой для функции Максвелла-Больцмана.
В проводниках, где концентрация электронов высока, электронный газ всегда находится в вырожденном состоянии. С невырожденным электронным газом приходится сталкиваться в собственных (беспримесных) и слаболегированных (1016...1024 м-3) полупроводниках. При таких условиях выполняется критерий (3.11) и электронный газ млжно считать невырожденным. Поэтому уместно, на наш взгляд, привести таблицу, где содержатся основные характеристики электронного газа: его средняя энергия, квадратичная скорость υкв, импульс P (табл. 3.2).
Таблица 3.2
Параметры электронного газа [15]
| Параметры газа | Газ | |
| невырожденный | вырожденный | |
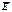 , Т =0
Т >0 , Т =0
Т >0
|

| 

|
| Jкв, Т =0 Т >0 |

|  м/с м/с
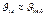
|
| Р, Т =0 Т >0 |

|  ≈1010 Па
Р ≈ Р 0 ≈1010 Па
Р ≈ Р 0
|
Из данных таблицы видно, что параметры вырожденного газа в отличие от газа невырожденного при нулевой температуре не равны нулю и практически не зависят от температуры. Это, в свою очередь, говорит о нетепловом квантовомеханическом характере данных процессов.






