31. Какая часть молекул водорода, находящегося при температуре T, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше чем на 5,0 м/с? Задачу решить для двух значений T: 1) 400 К, 2) 900 К.
Решение. Распределение молекул по скоростям выражается законом Максвелла: число молекул DN, относительные скорости которых лежат в интервале от u до u + Du:
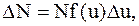
где N – полное число молекул газа;
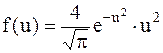– функция распределения Максвелла;
u=v/vв – относительная скорость;
v – данная скорость;
vв – наиболее вероятная скорость.
Закон распределения Максвелла оказывается справедливым при условии Du<u. Поскольку в задаче идет речь о наиболее вероятной скорости, надо считать v=vв. Следовательно, u=v/vв=1 и вышенаписанное уравнение примет более простой вид:
.
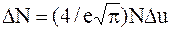Отсюда найдем ту часть молекул, относительные скорости которых лежат в интервале Du:
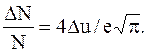
Прежде чем производить расчеты, необходимо убедиться в том, что выполняется условие Du<u. Так как u=v/vв , то Du=Dv/vв.
Чтобы вычислить Du, найдем сначала наиболее вероятную скорость при Т=400 К и Т=900 К по формуле:
:
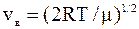vв1=2×8,31×400/0,002=1,82×103 м/с,
vв2=2×8,31×900/0,002=2,73×103м/с.
Подставляя эти значения vв и имея в виду, что Dv=10 м/с, поскольку в задаче идет речь о скоростях, лежащих в интервале от vв=-5,0 м/с до vв=5,0 м/с, получим:
Du1=1/182, Du2=1/273.
Так как u=1, видим, что условие Du<u выполняется для обеих температур.
Теперь найдем
DN1/N=4/((3,14)1/2×2,7×182)=0,0046,
DN2/N=4/((3,14)1/2×2,7×273)=0,0030.
Таким образом, при увеличении температуры наиболее вероятная скорость молекул увеличивается, а число молекул, скорости которых лежат в одном и том же интервале около наиболее вероятной, уменьшается.
Ответ: DN1/N=0,0046, DN2/N=0,0030.
32. Какая часть молекул газа имеет скорости превышающие наиболее вероятную?
Решение. В условии задачи речь идет о молекулах, скорости которых заключены в интервале от наиболее вероятной скорости v до v+Dv, т.е. в бесконечно большом интервале скоростей. Таким образом, условие применимости закона распределения скоростей, заключающееся в том, что Du<u, или Dv<v, здесь не выполняется. Поэтому от уравнения в форме:
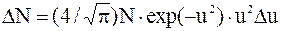
надо перейти к дифференциальной форме этого закона
Полное число DN молекул, относительные скорости которых лежат в заданном интервале от u1 до u2, найдем, интегрируя правую часть в этих пределах:
Данное уравнение является общей формой записи закона распределения скоростей молекул, справедливой для любых интервалов скоростей.
Учитывая, что относительная скорость u=v/vв и что в нашей задаче v1=vв и v2=4, получим: u1=1, и u2=¥. Следовательно, искомая часть молекул:
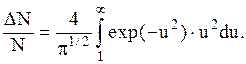
Чтобы избежать математических трудностей, связанных с нахождением неопределенного интеграла, воспользуемся тем очевидным фактом, что скорости всех молекул лежат в интервале от 0 до ¥. Поэтому, если обозначить через DN' число молекул, скорости которых меньше наиболее вероятной, т. е. лежат в интервале от 0 до 1, то можно записать:
.
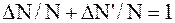Таким образом, вместо того, чтобы искать DN/N можно найти
,
а затем вычислить DN/N.
Так как зтот интеграл аналитически не вычисляется, то воспользуемся методом приближенного интегрирования. Для этого разложим подынтегральную функцию f(u)=exp(-u2)×u2 в ряд Маклорена:
exp(-u2)=1-u2/1+u4/2-u6/6+u8/24-...
exp(-u2) u2=u2-u4/1+u6/2-u8/6+u10/24-...
Теперь, произведя интегрирование, имеем:
DN'/N=4(1/3-1/5+1/14-1/54+1/264...)/p1/2.
Ограничиваясь первыми четырьмя членами разложения, найдем (с погрешностью, не превышающей 0,01):
DN'/N=0,43.
Тогда
DN/N=1-0,45=0,57.
Ответ: DN/N=0,57.
33. Найти число столкновений <z>, которые происходят в течение секунды между всеми молекулами, находящимися в объеме V=1,0 мм3 водорода при нормальных условиях. Принять для водорода d=2,3×10-10 м.
Решение. Число столкновений <z>, испытываемых одной молекулой за одну секунду, определяется по формуле
<z>= 2 1/2pd2×n2×<v>×V/2,
где d – эффективный диаметр молекулы;
n – концентрация молекул;
<v>= 
– средняя арифметическая скорость молекул газа.
Чтобы установить соотношение между величинами <z> и <z>, учтем, что если умножить число столкновений одной молекулы за одну секунду на число всех молекул N, то получим результат, превышающий в два раза искомое число <z>. Действительно, в одном столкновении участвуют сразу две молекулы, поэтому в число <z>×N каждое столкновение входит дважды: один раз в счет столкновений одной из молекул данной пары, другой раз в счет столкновений второй молекулы. Следовательно, правильным будет выражение
<z>=<z>N/2=<z>nV/2,
где n=p/kT – концентрация молекул.
Подставив вместо <z>, n и <v> их значение, окончательно получим:
<z>=2 1/2pd2p2V(8R/pmT)1/2/2k2T.
Выразим входящие в формулу величины в единицах СИ, подставив их в формулу и выполнив вычисление, будем иметь
<z>=1,6×1026 с-1.
Ответ: <z>=1,6×1026 с-1.
34. Пылинки массой m=10-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура T воздуха во всем объеме одинакова и равна 300 К.
Решение. При равновесном распределении пылинок концентрация их зависит только от координаты y по оси, направленной вертикально. В этом случае к распределению пылинок можно применить формулу Больцмана
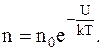
Так как в однородном поле силы тяжести U=mgy, то
По условию задачи, изменение Δn концентрации с высотой мало по сравнению с n (Dn/n=0,01), поэтому без существенной погрешности изменение концентрации n можно заменить дифференциалом dn.
Дифференцируя выражение по z, получим
Так как
,
то
dn=- mgndy/kT.
Отсюда находим интересующее нас изменение координаты:
dy=- kT dn/mgn.
Знак минус показывает, что положительным изменениям координаты (dy>0) соответствует уменьшение относительной концентрации (dn<0).
Знак минус опустим (в данном случае он несущественен) и заменим дифференциалы dy и dn конечными приращениями Dy и Dn:
Dy=kTDn/mgn.
Выразив входящие в формулу величины в системе СИ, подставив их в эту формулу, произведем вычисления
Dy=1,38×10-23×300×0,01/10-21×9,81=4,23×10-3 м=4,23 мм.
Ответ: Dy=4,23×10-3 м.
35. Барометр в кабине летящего самолета все время показывает одинаковое давление p=79 кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха за бортом самолета изменилась с t=5oC до t=1 oC. Какую ошибку h в определении высоты допустил летчик? Давление p у поверхности Земли считать нормальным.
Решение. Для решения задачи воспользуемся барометрической формулой
.
Барометр может показывать неизменное давление p при различных температурах T1 и T2 за бортом только в том случае, если самолет находится не на высоте h1 (которую летчик считает неизменной), а на некоторой другой высоте h2.
Запишем барометрическую формулу для двух случаев:
;
.
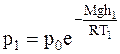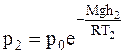Найдем отношение po/p и обе части полученных равенств прологарифмируем:
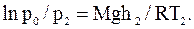
Из полученных соотношений выразим высоты h1 и h1 и найдем их разность
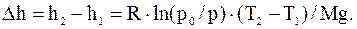
Проверим, дает ли правая часть полученного равенства единицу длины:
Выразив величины в СИ, подставив их в полученную формулу, произведем вычисления:
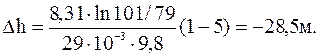
Ответ: Δh=-28,5 м.
36. Средняя длина свободного пробега <l> молекулы углекислого газа при нормальных условиях равна 40 нм. Определить среднюю арифметическую скорость <v> молекул и число <z> соударений, которые испытывает молекула в 1с.
Решение. Средняя арифметическая скорость молекул определяется по формуле
,
где m – молярная масса вещества.
Среднее число <z> соударений молекулы в одну секунду определяется отношением средней скорости <v> молекулы к средней длине ее свободного пробега <l>:
Размерность полученных величин очевидна. Подставив значения входящих в формулы величин в СИ, будем иметь
<v>=362 м/с;
<z>=9,05×109 с-1.
Ответ: <v>=362 м/с; <z>=9,05×109 с-1.
37. Вычислить удельные теплоемкости при постоянном давлении и при постоянном объеме неона и водорода, принимая газы за идеальные.
Решение. Между молярными и удельными теплоемкостями идеального газа при постоянном давлении и при постоянном объеме существует связь:
Cp=mcp и Cv=mcv,
где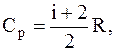 
а 
Таким образом, для удельных теплоемкостей имеем
а 
.
Зная, что неон одноатомный газ, то для него число степеней свободы i=3, m=20×10-3 кг/моль, а водород двухатомный газ для него число степеней свободы i=5, m=27×10-3 кг/моль. Подставляя в каждую из выше записанных формул значения числп степеней свободы и значение универсальной газовой постоянной, вычисляем удельные теплоемкости для:
1) неона
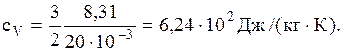
2) водорода
;
.
Ответ: 1) 
2) 
; 
.
38. Найти отношение удельных теплоемкостей при постоянном давлении и постоянном объеме для кислорода.
Решение. Отношение удельных теплоемкостей при постоянном давлении и постоянном объеме идеального газа равно отношению его молярных теплоемкостей при постоянном давлении и постоянном объеме:
Зная, что молярные теплоемкости при постоянном давлении и при постоянном объеме связаны с числом степеней свободы и равны:
и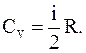 
Для отношения удельных теплоемкостей будем иметь
Кислород двухатомный газ, следовательно, число степеней свободы i=5. Подставляя значение i в вышезаписанную формулу, имеем
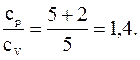
Ответ: сp/cV=1,4.
39. Удельная теплоемкость некоторого двухатомного газа равна 14,7 кДж/(кг×К). Найти молярную массу этого газа.
Решение. Известно, что удельная теплоемкость при постоянном давлении связана с молярной теплоемкостью газа:
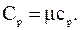
Молярная теплоемкость при постоянном давлении
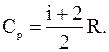
где i – число степеней свободы газа.
Таким образом:
Откуда
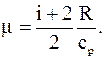
Подставляя в полученную формулу значения величин данных в условии задачи, с учетом того, что для двухатомного газа i=5, будем иметь:
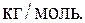
Ответ: μ=0,002 кг/моль.
40. Вычислить удельные теплоемкости при постоянном объеме и постоянном давлении смеси неона и водорода, если массовые доли неона и водорода составляют w1=80% и w2=20% соответственно. Удельные теплоемкости для неона сv=6,24×102 Дж/(кг×К), сp=1,04×103 Дж/(кг×К); для водорода – сv=1,04×104 Дж/(кг×К), сp=1,46×104 Дж/(кг×К).
Решение. В общем случае количество тепла необходимого для нагревания смеси газов, например, при нагревании в условиях постоянного объема от температуры Т1 до температуры Т2 равна:
где сv(см) – удельная теплоемкость смеси;
(m1+m2) – масса смеси;
(T2 -T1) – изменение температуры.
С другой стороны это количество тепла может быть вычислено по формуле:
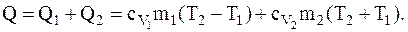
где Q1 и Q1 – соответственно количество тепла, которое необходимо сообщить,чтобы изменить температуру неона и водорода в отдельности;
сv1 и сv2 – удельные теплоемкости неона и водорода при постоянном объеме;
m1 и m2 – массы неона и водорода.
Таким образом, имеем:
или
.
Откуда
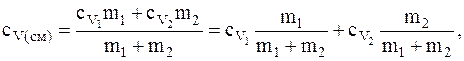
где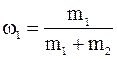 
и 
– массовые доли неона и водорода соответственно.
Подставляя численные значения для удельной теплоемкости смеси неона и водорода при постоянном давлении, будем иметь:
Аналогично можно получить формулу для определения удельной теплоемкости смеси неона и водорода при постоянном давлении:
.
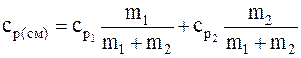Подставляя численные значения для удельной теплоемкости смеси при постоянном давлении, будем иметь:
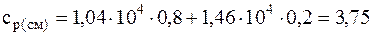
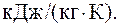
Ответ: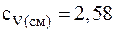 
; 
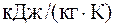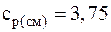
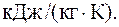
41. Кислород массой 2 кг занимает объем V1=1 м3 и находится под давлением p1=0,2 МПа (рис. 3.9). Газ был нагрет сначала при постоянном давлении до объема V2=3 м3, а затем при постоянном объеме до давления p3=0,5 МПа. Найти изменение внутренней энергии газа.
Решение. Изменение внутренней энергии газа
ΔU=cvmΔT,
где cv=iR/2μ – удельная теплоемкость при постоянном объеме;
μ – молярная масса газа;
ΔТ=(Т3-Т1) – изменение температуры газа в конечном и начальном состояниях;
i=5 – число степеней свободы (кислород двухатомный газ).
Температуру газа в начальном и конечном состояниях можно определить из уравнения Менделеева–Клапейрона:
.
Для начальной температуры
.
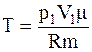Для конечной температуры
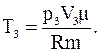
Тогда изменение внутренней энергии газа
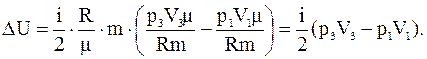
Подставляя численные значения, будем иметь
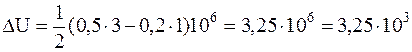Дж.
Ответ: ΔU=3,25 кДж.
42. Кислород массой 2 кг занимает объем V1=1 м3 и находится под давлением p1=0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2=3 м3, а затем при постоянном объеме до давления p3=0,5 МПа. Найти работу, совершенную газом, и теплоту, переданную газу (рис. 3.9).
Решение. Из уравнения Менделеева-Клапейрона
можно определить температуры, характерные для соответствующих состояний:
.
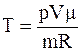Таким образом, температура газа в начальном состоянии
T1=p1V1m/mR;
в промежуточном
T2=p2V2m/mR;
в конечном
T3=p3V3 m/mR.
В процессе перехода газ совершал работу
A=A1+A2,
где A1 – работа газа, совершенная при переходе в условиях постоянного давления;
A2 – работа газа, совершенная при переходе в условиях постоянного объема.
Работа газа, совершенная при переходе в условиях постоянного давления определяется соотношением:
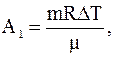
а работа газа, совершенная при переходе в условиях постоянного объема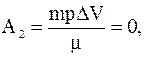 
т.к. DV=0.
Таким образом, в данном случае
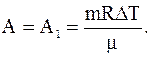
Количество тепла, переданного газу равно сумме изменения его внутренней энергии и работы, совершенной им:
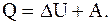
Известно, что изменение внутренней энергии газа пропорционально изменению его температуры, при этом
.
Следовательно, для изменения внутренней энергии газа при его переходе из начального в конечное состояние, имеем:
где DТ=T3–T1.
Таким образом, для количества тепла переданного газу имеем:
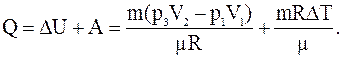
Подставив численные значения величин, будем иметь:
Т1=0,2×106×1×32×10–3/(8,31×103×2)=385 К;
Т2=0,2×106×3×32×10–3/(8,31×103×2)=1155 К;
Т3=0,5×106×3×32×10–3/(8,31×103×2)=2888 К;
DU=5×2×8,31×(2888–385)/(2×32×10–3)=3,25×103 Дж;
A=2×8,31×(1155–385)/32×10–3=0,4×103 Дж;
Q=3,25×103+0,4×103=3,65×103 Дж.
Ответ: A=Дж; Q=3,65×103 Дж.
43. Масса 10 г кислорода находится под давлением 0,3 МПа и при температуре 10 oС. После нагревания при постоянном давлении газ занял объем V2=10 л. Найти количество теплоты Q, полученное газом, и энергию теплового движения молекул газа W до и после нагревания.
Решение. Количество теплоты Q, полученное газом в процессе нагревания
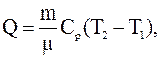
где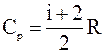 
– молярная теплоемкость газа при постоянном давлении;
i=5 – число степеней свободы (кислород двухатомный газ);
R=8,31 Дж/(моль×К) – универсальная газовая постоянная;
m=0,032 кг/моль – молекулярная масса кислорода;
T1 и T2 – температуры газа в начальном и конечном состояниях. Для определения температуры газа в конечном состоянии воспользуемся соотношением между температурой и объемом газа, нагреваемого в условиях постоянного давления:
.
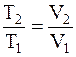Откуда
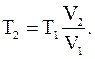
Воспользовавшись уравнением Менделеева–Клапейрона, записанным в виде
находим объем газа в начальном состоянии:
Для конечной температуры будем иметь соотношение:
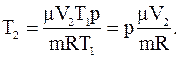
Подставляя численные значения, определяем конечную температуру газа:
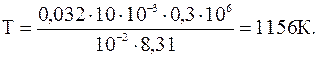
Подставляя численные значения, находим количество теплоты, полученное газом в процессе нагревания:
Энергию теплового движения молекул газа можно определить по формуле
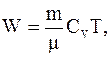
где CV=iR/2 – молярная теплоемкость газа при постоянном объеме.
Таким образом, для энергии теплового движения молекул газа в начальном состоянии имеем:
в конечном состоянии
.
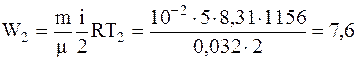
Ответ:Q=7,9 кДж; W1=1,8 кДж; W2=7,6 кДж.
44. Масса 12 г азота находится в закрытом сосуде объемом V=2 л при температуре t=10 oС. После нагревания давление в сосуде стало равным p2=1,33 МПа. Какое количество теплоты Q сообщено газу при нагревании?
Решение. Так как объем газа не изменился, то сообщенное ему количество теплоты пошло на изменение его внутренней энергии Q=DU, которое в свою очередь можно определить так:
DU=mCV(T2–T1)/m=mCVΔT/m,
где Cv=iR/2 – молярная теплоемкость азота при постоянном объеме.
Следовательно,
DU=miR(T2–T1)/2m.
Для определения конечной температуры T воспользуемся тем, что при нагревании газа в условиях постоянного объема отношение давлений пропорционально отношению его температур в начальном и конечном состояниях
p1/p2=T1/T2.
Имеем
T2=T1p2/p1.
Начальное давление определяем из уравнения Менделеева–Клапейрона, записанного для первоначального состояния:
p1V1=mRT1/m.
p1=mRT1/mV1.
Так как по условию задачи V1=V, то для конечной температуры имеем:
T2=mp2V/mR.
Подставляя значение T2 в формулу изменения внутренней энергии, которое равно количеству тепла, сообщенному газу, окончательно получим:
Q=imR(mp2V/mR-T1)/2m.
Размерность полученного результата очевидна. Численное значение Q равно
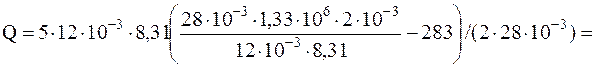=4,13 кДж.
Ответ: Q=4,13 кДж.
45. Баллон с кислородом емкостью V=20 л при давлении p=100 ат и температуре t=7 oС нагревается до t=27 oС. Какое количество теплоты при этом поглощает газ?
Решение. Поскольку коэффициенты теплового расширения для твердых тел значительно меньше (приблизительно в сто раз), чем для газов, в условиях данной задачи можно пренебречь расширением баллона и считать процесс нагревания газа изохорным.
При изохорных процессах, подводимое к системе количество тепла идет на изменение ее внутренней энергии.
Из определения молярной теплоемкости следует, что элементарное количество теплоты, сообщенное телу при повышении его температуры на dT, равно:
