Энергия, работа, мощность. Законы сохранения в механике.
Поле тяготения. Движение в поле центральных сил.
Элементы специальной теории относительности.
Примеры решения задач
1. Санки, движущиеся по горизонтальному льду со скоростью v=2 м/с, въезжают на асфальт (рис. 2.1). Считая, что длина полозьев санок равна ℓ=0,8 м, а коэффициент трения их об асфальт равен μ=0,2, определить путь S, пройденный санками по асфальту, если известно, что S>ℓ. Массу санок считать равномерно распределенной по длине полозьев. Трением санок о лед пренебречь.
Решение. Когда санки въезжают на асфальт, происходит постепенное увеличение силы давления N полозьев на асфальт от нуля до максимального значения, равного силе тяжести mg санок. В связи с этим возрастает и сила трения 
, действующая на санки со стороны асфальта.
Поскольку санки движутся под действием переменной силы, воспользуемся для решения задачи понятиями работы и энергии. Работа силы трения, действующей на санки, определяется изменением их кинетической энергии от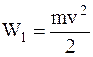 
до W2=0. Тогда на основании соотношения
можно записать
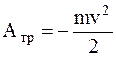. (1)
С другой стороны, работу Атр можно вычислить по формуле
,
где Fтр – сила трения;
α – угол между направлением движения и направлением, действующей силы. В рассматриваемом случае α=1800.
Для этого разобьем весь путь S, пройденный санками, на два участка S=ℓ+S'. На пути ℓ на санки действует переменная сила трения . Найдем совершенную ею работу А1. Пусть санки уже прошли по асфальту путь x (рис. 2.3), тогда сила давления полозьев на асфальт равна
,
сила трения
,
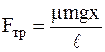а работа этой силы на пути ℓ
. (2)
Интеграл взят со знаком «минус» потому, что величина Fтр и dx имеют противоположные знаки. На пути S' сила трения постоянна и равна μmg, и поэтому совершаемая ею работа
.
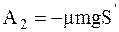Полная работа силы трения
. (3)
Приравнивая правые части равенств (1) и (3) и сокращая на массу, найдем
.
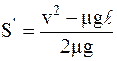Таким образом, весь путь, пройденный санями:
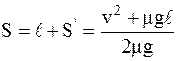. (4)
Теперь можем подставить числовые значения и произвести вычисления
м.
Ответ: S=1,42 м.
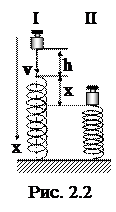
2. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на x0=1,0 мм. На сколько сожмет пружину эта же гиря, брошенная вертикально вниз с высоты h=0,20 м. Скорость гири принять равной v=1,0 м/с?
Решение. Искомая величина x деформации пружины определяется из формулы потенциальной энергии сжатой пружины:
.
Поэтому можно воспользоваться законом сохранения энергии. Так как на гирю действует сила тяжести, рассмотрим систему Земля-гиря-пружина. Поскольку при движении гири и сжатии пружины трения практически не возникает, полная механическая энергия этой изолированной системы будет сохраняться.
Подсчитаем энергию системы в ее начальном (I) и конечном (II) состояниях (рис. 2.2). Выберем за нулевой уровень отсчета высоты самое нижнее положение гири, соответствующее сжатой пружине. В начальном состоянии энергия системы W1 складывается из потенциальной и кинетической энергии гири:
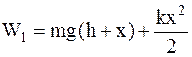. (1)
В конечном состоянии у гири не будет кинетической энергии, зато сжатая пружина будет обладать энергией упругой деформации. Таким образом, полная энергия системы W2 будет равна:
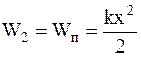, (2)
Где коэффициент упругой деформации k, согласно его определению, равен
. (3)
Приравнивая по закону сохранения энергии правые части выражений (1) и (2) с учетом соотношения (3), получим после простых преобразований квадратное уравнение относительно x:
.
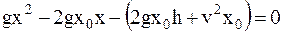Решив уравнение, найдем
.
Отрицательный корень не удовлетворяет условию задачи, так как x<0 означает растяжение пружины, тогда как на самом деле она сжимается.
Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:
м.
Ответ: x=8×10-2 м.
3. Небольшое тело соскальзывает вниз с высоты h=1,0 м по наклонному желобу, переходящему в «мертвую петлю» радиуса R=0,80 м (рис. 2.3). На какой высоте h' выпадает тело из петли? Трением пренебречь.
Решение. Сначала выясним, почему, двигаясь вдоль петли, тело может оторваться от нее. На тело в произвольный момент времени его движения вверх по петле действуют две силы: сила тяжести m g и сила давления N петли, направленная по радиусу к центру окружности. По второму закону Ньютона,
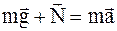. (1)
Направим оси проекций x и y по векторам нормального и тангенциального ускорений a n a τ, т.е. по радиусу и касательной к окружности. Учитывая, что
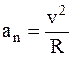и 
,
запишем вместо (1) два скалярных уравнений для осей x и y соответственно:
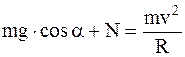, (2)
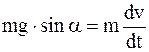. (3)
Так как при движении вверх по петле величина 
возрастает, а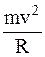 
убывает, то величина 
в уравнении (2) должна и подавно убывать. При обращении N в нуль тело оторвется от петли.
Приняв N=0, перепишем, сокращая величину m, уравнения (2) и (3) для момента отрыва тела от петли:
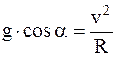, (2')
. (3')
В систему (2') и (3') явно не вошла искомая величина h', однако она весьма просто связана с углом α. Как видно из рис. 2.3,
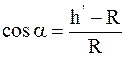. (4)
Поэтому было бы достаточно найти величину α. Однако найти ее из системы (2'), (3') невозможно, так как эта система содержит более двух неизвестных.
Так как трение отсутствует и, следовательно, на тело действуют только потенциальные силы, то полная механическая энергия тела (точнее: замкнутой системы тело-желоб-Земля) во время его движения будет сохраняться.
В начальный момент времени тело обладает только потенциальной энергией
W1=mgh.
В момент отрыва движущегося со скоростью v тела его полная энергия
W2=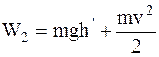 
.
Приравняв по закону сохранения энергии величины W1 и W2, получим
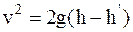. (5)
Теперь из (2'), (4) и (5), будем иметь
.
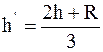Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получи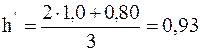м:
м.
Ответ: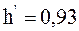 
м.
Замечание. Необходимо отметить, что тело выпадает из петли не при любых значениях h. Действительно, так как h' не может быть больше 2R и меньше R (при h'<R, даже полностью потеряв скорость, тело, не отрываясь от петли, начнет скользить обратно), т.е. h'max=2R и h'min=R, то подставив эти значения h' в (6), получим:
, 
.
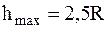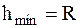Следовательно, при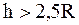 
, 
тело из петли не выпадает.
4. На железнодорожной платформе, движущейся по инерции со скоростью v=10 м/с, укреплено орудие, ствол которого направлен в сторону движения платформы и приподнят над горизонтом на угол α=300 (рис. 2.4). Орудие произвело выстрел, в результате чего скорость платформы с орудием уменьшилась в 3 раза. Найти скорость v' снаряда (относительно орудия) при вылете из ствола. Масса снаряда m=10 кг, платформы с орудием M=1000 кг.
Решение. На систему платформа с орудием–снаряд извне действуют две силы: сила тяжести системы 
и сила нормального давления N рельсов. До выстрела эти силы уравновешивались, так как система двигалась равномерно. Во время выстрела сила взаимодействия между платформой и рельсами возрастает вследствие явления отдачи, поэтому равновесие сил, приложенных к системе, нарушается:
.
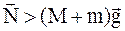Следовательно, во время выстрела система не является замкнутой, ее импульс изменяется. Однако обе рассматриваемые силы действуют по вертикали, в то время как в горизонтальном направлении никакие силы на систему не действуют (трением платформы о рельсы пренебрегаем). Поэтому проекция импульса системы на горизонтальное направление (на ось x) есть величина постоянная:
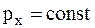. (1)
Пусть состояниям системы до и после выстрела соответствуют значения величины 
, равные 
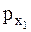и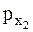 
. Рассматривая все движения относительно Земли, получим:
, (2)
, (3)
где 
– проекция на ось x скорости vс снаряда относительно Земли.
Чтобы связать величину vс с искомой скоростью v', будем рассматривать движение снаряда относительно Земли как сложное, состоящее из двух: со скоростью v ' относительно орудия и со скоростью v /3 вместе с орудием относительно Земли.
Тогда в соответствии с законом сложения скоростей будем иметь:
. (4)
Спроектируем векторы, входящие в (4), на ось x:
. (5)
Заменив в (3) величину ее значением по (5) и приравняв согласно (1) правые части формул (2) и (3), найдем
.
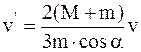Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:
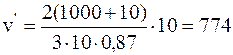м/с.
Ответ: v'=774 м/с.
5. На корме лодки длиной ℓ=200 см и массой M=120 кг сидит человек массой m=80 кг. В результате кратковременного толчка лодка с человеком приобретает скорость v0=2 м/с и начинает двигаться от одного берега канала шириной d=10 м к другому берегу (рис. 2.5), при этом человек переходит с кормы на нос лодки. Пренебрегая сопротивлением воды, найти время движения лодки.
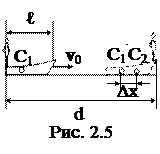Решение. Рассматривая систему лодка–человек как замкнутую и применяя закон сохранения импульса 
, приходим к выводу, что, поскольку закон движения человека относительно лодки нам неизвестен, движение лодки относительно воды (или Земли) нельзя считать равномерным. Однако на основании соотношения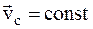 
можно утверждать, что скорость центра масс системы относительно воды есть величина постоянная: 
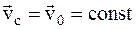. Отсюда следует, что искомое время
, (1)
где С1 и С2 – начальное и конечное положения центра инерции системы;
v0 – скорость центра инерции.
Из формулы (1) следует, что ответ не зависит от характера движения человека. Предположим, что оно было равномерным в течение всего промежутка времени. Тогда будет равномерным и движение лодки. Пусть p 0 и p – импульсы системы соответственно в начальный и некоторый промежуточный моменты времени. Тогда, по закону сохранения импульса,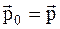 
, т.е.
, (2)
где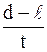 
–скорость лодки;
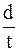–скорость человека (все скорости даны в системе отсчета, связанной с Землей).
Решив уравнение (2) относительно t, получим
.
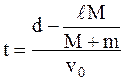Выразив величины, входящие в формулу, в единицах СИ и подставив их числовые значения, получим:
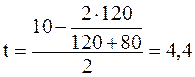с.
Ответ: t=4,4 с.
6. На спокойной воде пруда стоит лодка, длиной L и массой M, перпендикулярно берегу, обращенная к нему носом. На корме стоит человек массой m. На какое расстояние S удалится лодка от берега, если человек перейдет с кормы на нос лодки? Трением о воду и о воздух пренебречь.
Решение. Для простоты решения будем считать, что человек идет по лодке с постоянной скоростью. Лодка в этом случае также будет двигаться равномерно. Поэтому путь s, пройденный лодкой относительно берега, определим по формуле:
,
где v – скорость лодки относительно берега;
t – время движения лодки.
Скорость v лодки найдем, пользуясь законом сохранения импульса (количества движения). Так как по условию задачи система человек-лодка изолированная и в начальный момент относительно берега была в покое, то по закону сохранения импульса, опустив знак минус, получим:
,
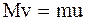где u – скорость человека относительно берега.
Отсюда
.
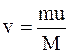Время t движения лодки равно времени перемещения человека по лодке, т.е.
,
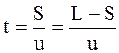где S – путь, пройденный человеком относительно берега.
Подставив полученные выражения v и t, найдем
.
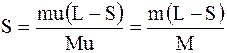Откуда
.
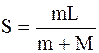Ответ: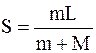 
.
7. При выстреле из пружинного пистолета вертикально вверх пуля массой 20г поднялась на высоту 5 м. Определить жесткость k пружины пистолета, если она была сжата на 10 см. Массой пружины пренебречь.
Решение. Для решения задачи воспользуемся законом сохранения энергии в механике. Но прежде проследим за энергетическими превращениями, с которыми связан выстрел.
При зарядке пистолета сжимается пружина. При этом совершается работа A1, в результате чего пружина приобретает потенциальную энергию Wp1. При выстреле потенциальная энергия пружины переходит в кинетическую энергию WK2 пули, затем при подъеме ее на высоту h превращается в потенциальную энергию Wp2 пули.
Если пренебречь потерями энергии в этой цепочке энергетических превращений, то на основании закона сохранения энергии можно записать
А=Wp2.
Выразим работу А1. Сила F 1, сжимающая пружину, является переменной. В каждый данный момент времени она по направлению противоположна силе упругости F и численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука:
F=-kx,
где x – абсолютная деформация пружины.
Работу переменной силы вычислим как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой
dA1=F1×dx,
или
dA1=kx×dx.
Интегрируя в пределах от 0 до s, получим
.
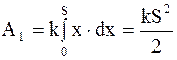Потенциальная энергия пули на высоте h определяется по формуле
W2=mgh,
где g – ускорение свободного падения.
Таким образом, имеем
.
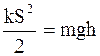Откуда
.
Теперь можем подставить числовые значения и произвести вычисления
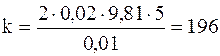Н/м=0,2 кН/м.
Ответ: k=0,2 кН/м.
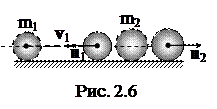8. Шар массой m1, движущийся горизонтально с некоторой скоростью v1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный (рис. 2.6). Какую долю своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
,
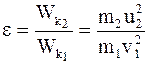где Wk1 – кинетическая энергия первого шара до удара;
v1 – скорость первого шара до удара;
Wk2 – кинетическая энергия второго шара после удара;
u2 – скорость второго шара после удара.
Как видно, для определения e надо найти u2. При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закон сохранения импульса и закон сохранения энергии в механике. Пользуясь этими законами, найдем u2.
По закону сохранения импульса, учитывая, что второй шар до удара покоился, имеем:
.
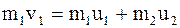По закону сохранения энергии
.
Решая совместно данные уравнения, найдем
.
Подставив это выражение в формулу для определения доли e энергии, сократив на v1 и m1, получим
.
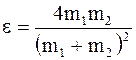Как видно из полученного соотношения, доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.
Ответ: 
.
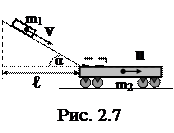9. Ящик массой m1=20 кг соскальзывает по идеально гладкому лотку длиной l=2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2=80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении (рис. 2.7). Определить скорость u тележки с ящиком, если лоток наклонен под углом a=30o к рельсам.
Решение. Тележку и ящик можно рассматривать как систему двух неупруго взаимодействующих тел. Но эта система не замкнута, так как сумма внешних сил, действующих на систему: двух сил тяжести m1 g и m2 g и силы реакции N 2, не равна нулю. Поэтому применить закон сохранения импульса к системе "ящик – тележка" нельзя.
Но так как проекция суммы указанных сил на направление оси x, совпадающей с направлением рельсов, равна нулю, то составляющую импульса системы в этом направлении можно считать постоянной, т.е.
,
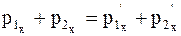где p1x и p2x – проекции импульса ящика и тележки с песком в момент падения ящика на тележку;
p1x¢и p2x¢ – те же величины после падения ящика.
Выразим в выше записанном равенстве импульсы тел через их массы и скорости, учтя при этом, что p2x=0 (тележка до взаимодействия с ящиком покосилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью u:
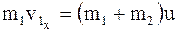
или
,
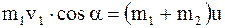где v1 – скорость ящика перед падением на тележку;
v1x=v1×cosa – проекция этой скорости на ось x.
Отсюда выразим искомую скорость:
.
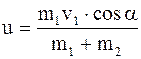Скорость v1 ящика перед падением определим из закона сохранения энергии
,
где h=l×sina.
После сокращения на m1 найдем
.
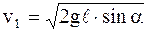Подставив найденное выражение для v1 в формулу для скорости u, получим
.
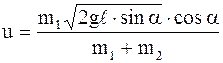Предварительно проверив размерность полученного результата, подставим числовые значения и произведем вычисления:
м/с.
Ответ: u=0,77 м/с.
10. При упругом ударе нейтрона о ядро углерода он движется после удара в направлении, перпендикулярном к начальному. Считая, что масса М ядра углерода в n=12 раз больше массы m нейтрона, определить, во сколько раз уменьшается энергия нейтрона в результате удара.
Решение. Введем обозначения: v – скорость нейтрона до удара, v ' – скорость нейтрона после удара, V – скорость ядра углерода после удара (до удара она равна нулю).
В результате упругого удара импульс и энергия, которыми до удара обладал нейтрон, распределяются между двумя частицами. При этом по законам сохранения импульса и энергии соответственно имеем:
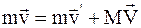, (1)
. (2)
По условию задачи требуется найти отношение
.
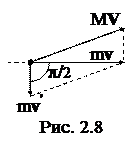Для выполнения расчетов необходимо перейти от векторной формы записи уравнения (1) к скалярной форме. Это можно сделать, применив метод проекций, который неоднократно использовался. Однако в данном случае можно поступить проще. Изобразим на рисунке 2.8 импульсы m v ', M V и их векторную сумму m v, учитывая, что угол между векторами m v и m v ' равен π/2. Из треугольника импульсов имеем
. (3)
Почленно разделив уравнение (2) на m и (3) на m2 и учитывая условие M/m=n, получим:
, (4)
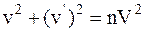. (5)
Чтобы исключить из системы величину V, разделим почленно (5) на (4):
,
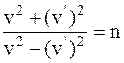а числитель и знаменатель полученного соотношения на (v')2, тогда находим
,
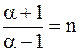откуда
.
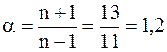Ответ: α=1,2.
11. Молот массой 5,00 кг, двигаясь со скоростью v=4,00 м/с, ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием равна M=95 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на ковку (деформацию) изделия. Чему равен КПД процесса ковки при данных условиях?
Решение. Строго говоря, система молот–изделие–наковальня не является замкнутой. На нее действуют извне сила тяжести (M+m)g и сила давления N опоры, на которой стоит наковальня. Во время удара молота вторая сила в той или иной степени, определяемой упругими свойствами опоры, будет превышать первую силу и к рассматриваемой системе будет приложена извне равнодействующая
R=N-(M+m)g.
Однако силы ударного взаимодействия тел весьма велики. Очевидно, условие задачи предполагает, что по сравнению с этими силами величиной R можно пренебречь, и, таким образом, считать систему замкнутой.
На основании закона сохранения энергии можно утверждать, что энергия, затраченная на деформацию изделия, равна разности значений механической энергии до и после удара. Так как во время удара изменяется только кинетическая энергия тел (незначительным перемещением тел по вертикали за время удара мы пренебрегаем), то для энергии деформации получаем
, (1)
где v'–общая скорость всех тел системы после неупругого удара, которую можно определить на основании закона сохранения импульса:
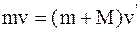. (2)
.
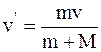Подставив в формулу (1) значение v', получим:
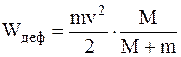. (3)
Так как энергия, расходуемая на ковку изделия, является по смыслу задачи полезной, то КПД процесса ковки
. (4)
Подставив числовые значения заданных величин в формулы (3) и (4) и выполнив вычисление, получим:
Дж;
.
Ответ: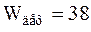 
Дж;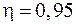 
.
Замечание. Из формулы (4) видно, что КПД процесса ковки тем больше, чем больше масса наковальни по сравнению с массой молота. При (m/M)®0 η®1.
12. Маховик, выполненный в виде диска радиусом 0,4 м и имеющий массу 1 кг, раскручен до скорости вращения 480 об/мин и предоставлен самому себе. Под действием трения вала о подшипники он до полной остановки сделал 240 оборотов. Определить момент сил трения вала о подшипники.
Решение. Так как в условии задачи дано число оборотов, сделанных маховиком до полной остановки, то воспользуемся уравнением, выражающим связь между работой и изменением кинетической энергии, для вращательного движения:
А=DWkвр,
где А=М×j – работа сил трения;
– изменение кинетической энергии;
j – угол поворота;
– момент инерции маховика относительно данной оси вращения;
w1 и w2 – начальная и конечная угловые скорости маховика, при этом w2 =0.
Имеем
.
Размерность полученного результата очевидна. Подставим в полученное для M2 выражение числовые значения входящих величин и произведем вычисления:
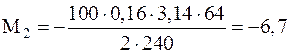Нм.
Знак «минус» означает, что на маховик действительно действуют силы трения.
Ответ: М2=-6,7 Нм.
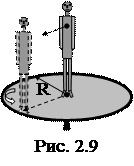13. Платформа в виде сплошного диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1 (рис. 2.9). В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение. Платформа вращается по инерции. Следовательно, момент внешних сил относительно оси вращения z, совпадающей с гео- метрической осью платформы, равен нулю. При этом условии момент импульса Lz системы "платформа-человек" остается постоянным:
Lz=Izw=const,
где Iz – момент инерции платформы с человеком относительно оси z;
w – угловая скорость платформы.
Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому
Iz=I1+I2,
где I1–момент инерции платформы;
I2–момент инерции человека.
С учетом этого имеем
(I1+I2)w=const
или
(I1+I2)w=(I1¢+I2¢)w¢,
где нештрихованные значения величин относятся к начальному состоянию системы, штрихованные – к конечному состоянию.
Момент инерции платформы (сплошного диска) относительно оси z при переходе человека не изменятся:
.
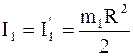Момент инерции человека будет изменяться. Если человека рассматривать как материальную точку, то его момент инерции Iz в начальном положении (в центре платформы) можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека
.
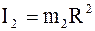Подставим в формулу закона сохранения найденные выражения моментов инерции, начальную угловую скорость вращения платформы с человеком, выраженную через частоту вращения n (w=2pn) и конечную угловую скорость, выраженную через линейную скорость v человека относительно пола (w¢=v/R), получим:
.
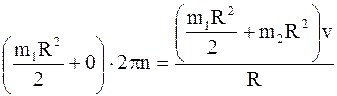После простых преобразований находим интересующую нас скорость:
.
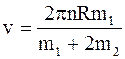Проверив размерность полученного результата, подставим числовые значения физических величин в системе СИ, произведем вычисления:
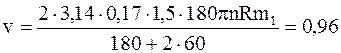м/с.
Ответ: v=0,96 м/с.
14. Круглая платформа радиуса R=1,00 м, момент инерции которой I=130 кг×м2, вращается по инерции вокруг вертикальной оси, делая n1=1,00 об/с. На краю платформы стоит человек, масса которого m=70 кг (рис. 2.10). Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки.
Решение. Перемещаясь по платформе, человек взаимодействует с ней. О характере этого взаимодействия нам ничего не известно, поэтому основное уравнение динамики вращательного движения к платформе применить невозможно. В этой задаче нет оснований и для применения закона сохранения энергии, поскольку не исключено, что, перемещаясь по вращающейся платформе, человек будет совершать работу, изменяя механическую энергию вращающейся системы платформа–человек.
Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы платформа–человек выполняется закон сохранения момента импульса, который запишем так:
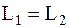. (1)
Начальный момент импульса системы L1 (человек стоит на краю платформы) и конечный момент импульса L2 (человек стоит в центре платформы) соответственно равны:
; (2)
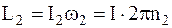, (3)
где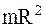 
– момент инерции человека;
– начальный момент инерции системы;
I – момент инерции платформы;
ω1 – начальная угловая скорость системы;
n1 – начальное число оборотов системы;
I2=I – конечный момент инерции системы;
ω2 – конечная угловая скорость системы;
n2 – конечное число оборотов системы.
Решая систему уравнений (1)–(3), для конечного числа оборотов системы будем иметь:
.
Проверив размерность полученного результата, подставив числовые значения физических величин в системе СИ, произведем вычисления:
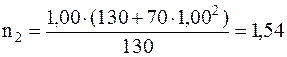об/с.
Ответ: n2=1,54 об/с.
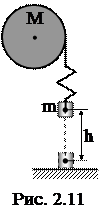15. Маховик, имеющий вид диска радиуса R и массы М, может вращаться вокруг горизонтальной оси. К его цилиндрической поверхности прикреплен шнур, к другому концу которого подвешен груз массы m. Груз был поднят и затем отпущен. Упав свободно с высоты h, груз натянул шнур и благодаря этому привел маховик во вращение (рис. 2.11). Какую угловую скорость ω приобрел при этом маховик?
Решение. Когда падающий груз натягивает шнур, возникает взаимодействие посредством шнура между грузом и маховиком. Характер взаимодействия зависит от упругих свойств тел (в основном шнура). В результате этого взаимодействия увеличивается скорость точек цилиндрической поверхности маховика и уменьшается скорость падения гири. Шнур растягивается до тех пор пока эти скорости не станут одинаковыми. Такое кратковременное взаимодействие груза и маховика можно рассматривать как неупругий удар. При неупругом ударе закон сохранения механической энергии не выполняется. Следовательно, для решения этой задачи данный закон неприменим. Однако к системе груз–маховик можно применить закон сохранения момента импульса.
На рассматриваемую систему действуют три внешних силы: сила тяжести маховика, реакция опоры и сила тяжести груза. Поскольку две первые силы проходят перпендикулярно оси диска, их момент относительно этой оси равен нулю. Действием же момента силы тяжести груза, равного mgR, во время удара можно пренебречь по сравнению с моментом сил взаимодействия груза и маховика при ударе. Таким образом, можно считать, что результирующий момент всех внешних сил относительно оси маховика во время удара равным нулю. Тогда, по закону сохранения момента импульса,
, (1)
где L1 и L2 – моменты импульса системы груз – маховик соответственно в начале и в конце удара.
Так как в начале удара диск был еще неподвижен, величина L1 представляет собой момент импульса падающего груза относительно оси вращения маховика. Принимая груз за материальную точку, можно записать
, (2)
где v1 – скорость гири, которую можно найти по известной формуле скорости при свободном падении:
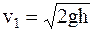. (3)
Величина L2 равна суммарному моменту импульса гири и вращающегося маховика, когда скорости груза и точек цилиндрической поверхности диска стали одинаковыми:
, (4)
где величины v2 и ω связаны соотношением
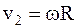. (5)
Подставив в уравнение (1) значения L1 и L2. Решив его относительно ω с учетом формул (3), (5) и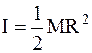 
, получим
.
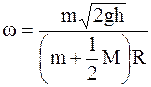Ответ: 
.
16. Маятник в виде однородного шара, жестко скрепленный с тонким стержнем, длина которого равна радиусу шара, может совершать колебательные движения вокруг горизонтальной оси, проходящей через конец стержня (рис. 2.12). В шар нормально к его поверхности ударилась пуля массы m=10,0 г, летевшая горизонтально со скоростью v=800 м/с, и застряла в шаре. Масса шара М=10,0 кг, его радиус R=15 см. На какой угол α отклонится маятник в результате удара пули? Массой стержня пренебречь.
Решение. Как видно из рисунка, искомый угол α связан с высотой h подъема центра шара:
. (1)
Так как величина h определяет потенциальную энергию, полученную шаром вследствие удара пули. Поскольку в результате удара пули в шар скорости обоих тел будут одинаковыми, то удар следует считать неупругим. Следовательно, механическая энергия в процессе удара не сохраняется (частично переходит во внутреннюю энергию). Однако после удара механическая энергия движущейся системы маятник–пуля будет сохраняться, так как теперь в ней действуют только потенциальные силы. Таким образом, при подъеме шара вместе с пулей кинетическая энергия вращательного движения системы будет превращаться в потенциальную энергию поднятых тел. По закону сохранения энергии,
, (2)
где I – момент инерции маятника вместе с застрявшей в нем пулей;
h' – высота подъема пули.
По условию задачи M>>m, поэтому, пренебрегая массой пули по сравнению с массой шара, величиной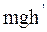 
в уравнении (2) можно пренебречь.
Для момента инерции маятника, на основании теоремы Штейнера, будем иметь:
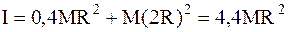. (3)
Для определения угловой скорости ω воспользуемся законом сохранения момента импульса. Его применение основано на том, что во время удара на систему маятник–пуля извне действуют силы тяжести и реакции опоры. Вторая сила проходит перпендикулярно оси маятника, поэтому ее момент равен нулю. Учитывая, что за время удара маятник не успевает заметно отклониться от вертикали, и принимая во внимание условие M>>m, можно считать, что и первая сила во время удара тоже проходит перпендикулярно оси вращения. Следовательно, ее момент также равен нулю.
Согласно закону сохранения момента импульса системы во время удара, должно выполняться соотношение:
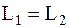, (4)
где 
, и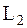 
– моменты импульса системы соответственно в начале м в конце процесса удара.
Величина есть момент импульса летящей пули относительно оси вращения маятника (сам маятник пока еще неподвижен). На основании определения имеем
. (5)
Момент импульса 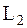маятника с застрявшей в нем пулей, согласно определению, равен
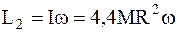. (6)
Решая систему уравнений (4)–(6), получаем для угловой скорости
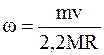. (7)
Исключив из системы (1)–(3), (7) неизвестные I, ω и h, найдем
.
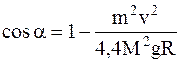Подставив в эту формулу числовые значения величин, выраженные в единицах СИ, и произведя вычисления, получим:
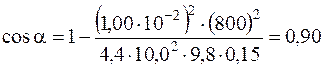; α=260.
Ответ: α=260.
17. Через блок, выполненный в виде диска и имеющий массу m=80 г, перекинута тонкая, гибкая нить, к концам которой подвешены грузы с массами m1=100 г и m2=200 г (рис. 2.13). С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение. Применим к решению задачи закон сохранения энергии, согласно которому при отсутствии трения полная энергия изолированной системы остается неизменной. Энергия при этом может превращаться только из потенциальной в кинетическую, и наоборот. Напомним, что в механике полной энергией тела называется сумма его потенциальной и кинетической энергий.
Предположим, что в начальный момент движения потенциальная энергия первого груза была равна Wp1, второго – Wp2. Через некоторое время высота первого груза увеличилась на h, второго уменьшилась на h. Потенциальная энергия первого груза стала равна
W1=Wp1 + m1gh,
второго
W2=Wp2 – m2gh.
Кроме того, каждый из грузов, двигаясь с ускорением a, приобрел за это время скорость v и кинетическую энергию, равную соответственно
и 
.
Точно так же диск, вращаясь равноускоренно, приобрел угловую скорость и соответствующую ей кинетическую энергию
,
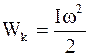где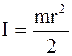 
– момент инерции диска;
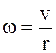– угловая скорость.
Тогда для кинетической энергии диска, после соответствующих преобразований, будем иметь
.
По закону сохранения энергии
.
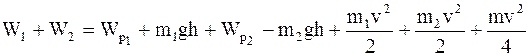Так как грузы двигались равноускоренно, то 
.
Подставив значение скорости, решая полученное уравнение
,
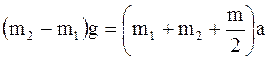будем иметь
.
Отношение масс в правой части полученной формулы – величина безразмерная. Поэтому числовые значения масс m1, m2 и m можно взять в граммах, как они даны в условии задачи. Числовое значение ускорения g надо взять в единицах системы СИ. Размерность полученного результата очевидна. После подстановки получим
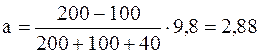м/с2.
Ответ: a =2,88 м/с2.
18. Тонкий однородный стержень длиной ℓ может вращаться вокруг горизонтальной оси, проходящей через конец стержня перпендикулярно ему. Стержень отклонили на 900 от положения равновесия и отпустили. Определить скорость v нижнего конца стержня в момент прохождения положения равновесия.
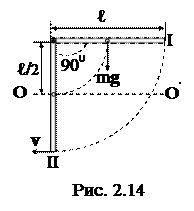Решение. Стержень поворачивается вокруг оси под действием момента силы тяжести. Так как при опускании стержня этот момент уменьшается, вращение стержня не будет равнопеременным, поэтому применение основного уравнения динамики вращательного движения здесь нецелесообразно.
Воспользуемся законом сохранения энергии. Так как в данном случае отсутствуют силы трения, энергия стержня (точнее, системы стержень–Земля) не изменяется при его движении, поэтому
,
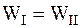где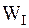 
– потенциальная энергия поднятого стержня,, если принять нулевой уровень отсчета высоты ОО', (рис. 2.14) проходящим через центр тяжести стержня в его нижнем положении;
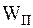– кинетическая энергия его вращательного движения.
Следовательно,
, 
.
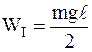Приравнивая правые части последних равенств и учитывая, что момент инерции стержня относительно оси, проходящей через его конец, на основании теоремы Штейнера равен
,
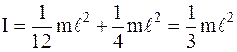а также что
,
для искомой скорости получим
.
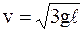Ответ: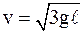 
.
19. Система, состоящая из цилиндрического катка радиуса R и гири, связанных нитью, перекинутый через блок (рис. 2.15.), под действием силы тяжести гири приходит в движение из состояния покоя. Определить ускорение а центра инерции катка и силу натяжения Т нити. Какую скорость v приобретет гиря, если она опустится с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Считать, что цилиндр катится по горизонтальной поверхности без скольжения. Трением качения пренебречь.
Решение. Анализируя условие задачи, выясняем, что на каток действует сила трения. Несмотря на это, к системе каток–гиря можно применить закон сохранения механической энергии, поскольку эта сила – сила трения покоя. В отличие от силы трения скольжения и трения качения эта сила не совершает работы, связанной с убылью механической энергии системы.
Начальная энергия системы W1 есть потенциальная энергия системы поднятая гиря–Земля. При этом, поскольку потенциальная энергия системы каток–Земля во время движения катка не изменяется, то ее можно не учитывать при составлении уравнения, выражающего закон сохранения энергии. Выберем нулевой уровень отсчета высоты проходящим через центр тяжести опущенной гири (xx'). Тогда получим
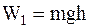. (1)
Будем рассматривать качение цилиндра как результат двух движений: поступательного со скоростью центра инерции и вращательного вокруг оси, проходящей через центр инерции. Тогда конечная энергия системы, когда гиря опустится с высоты h, будет равна
. (2)
Первые два члена в правой части формулы (2) выражают кинетическую энергию поступательного и вращательного движений катка. На основании закона сохранения энергии (
) имеем
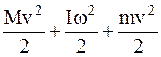. (3)
Учитывая соотношения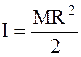 
и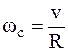 
, из уравнения (3) найдем скорость гири:
. (4)
Определим ускорение центра инерции катка, равное ускорению гири, приняв во внимание, что рассматриваемая система движется под действием постоянных сил и, следовательно, ее ускорение постоянно. Сравнивая выражение (4) с формулой скорости равнопеременного движения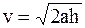 
, для ускорения получим
.
Для вычисления силы натяжения Т нити еще раз воспользуемся законом сохранения энергии. На основании этого закона работа, совершенная силой Т, приложенной к центру инерции катка, при перемещении последнего на расстояние ℓ=h равна кинетической энергии, полученной катком при этом перемещении, т.е.
.
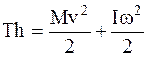Отсюда, учитывая соотношения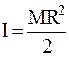 
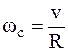, и , найдем силу Т:
.
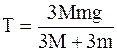Ответ: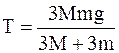 
.
20. Частица массой m=0,01 кг совершает гармонические колебания с периодом T=2с. Полная энергия колеблющейся частицы W=0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F, действующей на частицу.
Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы
,
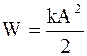где k=mw2 – коэффициент квазиупругой силы;
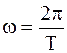– круговая или циклическая частота.
Подставив значения k и w в формулу полной энергии, выразим амплитуду
.
Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением
F=-kx,
где x – смещение колеблющейся точки.
Максимальное значение сила приобретает при максимальном смещении, равном амплитуде, т.е.
Fmax=kА.
Коэффициент k выразим через период колебаний:
.
Подставив в уравнение для максимальной силы значения k и А, после сокращений и упрощений, получим
.
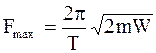Проверив размерность полученных результатов, подставим числовые значения величин, произведем вычисления:
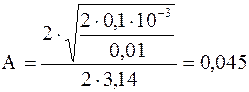м,
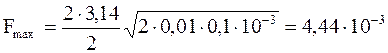Н.
Ответ: А=45 мм; Fmax=4,44 мН.
21. Определить вторую космическую скорость ракеты, запущенной с поверхности Земли.
Решение. Второй космической (или параболической) скоростью называется минимальная скорость, которую нужно сообщить телу, чтобы оно удалилось с поверхности Земли в бесконечность (при этом сопротивление воздух в расчет не принимается и предполагается, что на тело действует только поле тяготения Земли).
При удалении тела массой m в бесконечность его потенциальная энергия возрастает за счет убыли кинетической энергии и в бесконечности достигает максимального значения, равного нулю. Согласно определению второй космической скорости, кинетическая энергия в бесконечности также равна нулю. Таким образом, в бесконечности Wpб=0 и Wkб=0. В соответствии с законом сохранения энергии в механике
Wk + Wp=Wkб + Wpб,
или
,
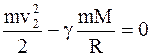где М – масса Земли;
R – радиус Земли.
Находим
.
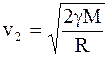Преобразуем полученную формулу, умножив и разделив подкоренное выражение на R:
.
Так как
,
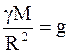где g – ускорение свободного падения у поверхности Земли, то
.
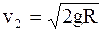Подставив в эту формулу значения g и R и производя вычисления, получим
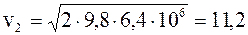км/c.
Ответ: v2=11,2 км/с.
22. Ракета установлена на поверхности Земли для запуска в вертикальном направлении. При какой минимальной скорости, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли (R=6,4 ×106 м)? Силами, кроме гравитационного взаимодействия ракеты и Земли, пренебречь.
Решение. Чтобы определить минимальную скорость v1 ракеты, надо найти ее минимальную кинетическую энергию Wk. Для этого воспользуемся законом сохранения механической энергии. Этот закон выполняется для замкнутой системы тел, в которой действуют только консервативные силы. Систему "ракета – Земля" можно считать замкнутой. Единственная сила, действующая на систему, – сила гравитационного взаимодействия, является консервативной.
В качестве системы отсчета выберем инерциальную систему отсчета, так как только в такой системе справедливы законы динамики и, в частности, законы сохранения. Известно, что система отсчета, связанная с центром масс замкнутой системы тел, является инерциальной. В рассматриваемом случае центр масс системы «ракета – Земля» будет практически совпадать с центром Земли, так как масса Земли M много больше массы m ракеты. Следовательно, систему отсчета, связанную с центром Земли, можно практически считать инерциальной. Согласно закону сохранения механической энергии, запишем
Wp1 + Wk1=Wp2 + Wk2,
где Wp1 и Wk1 – кинетическая и потенциальная энергии системы "ракета-Земля" в начальном состоянии (на поверхности Земли);
Wp2 и Wk2 – те же величины в конечном состоянии (на расстоянии, равном радиусу Земли).
В выбранной системе отсчета кинетическая энергия Земли равна нулю. Поэтому Wk1 есть просто начальная кинетическая энергия ракеты
.
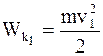Потенциальная энергия системы в начальном состоянии (потенциальная энергия гравитационного взаимодействия тел, бесконечно удаленных друг от друга, принимается равной нулю)
.
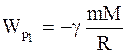По мере удаления ракеты от поверхности Земли потенциальная энергия Wp будет возрастать, кинетическая энергия – убывать. В конечном состоянии кинетическая энергия Wk станет равной нулю, потенциальная энергия Wp при r=2R достигнет значения
.
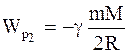Подставив значения Wk1, Wp1, Wk2, Wp2 в выше написанную формулу закона сохранения механической энергии, будем иметь
.
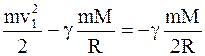Откуда после сокращения на m найдем
,
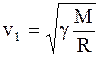а так как 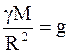, то
.
Подставив числовые значения величин, и произведя вычисления, получим
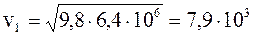м/с.
Полученный результат совпадает с выражением для первой космической скорости.
Ответ: v1=7,9×103 м/с.
23. Найти выражение для потенциальной энергии Wp гравитационного взаимодействия Земли и тел массой m, находящегося на расстоянии r от центра Земли за пределами ее поверхности.
Решение. Потенциальная энергия в поле консервативных сил (гравитационные силы консервативны) связана с силой, следующим соотношением:
,
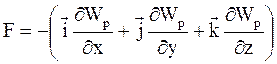где i, j, k – единичные векторы осей координат (орты);
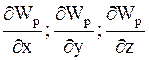- частные производные потенциальной энергии по соответствующим координатам.
В случае, когда поле сил обладает сферической симметрией, это выражение упрощается. Если ось x совместить с радиус-вектором r, направленным по радиусу сферы, то
; 
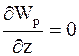
и тогда
.
Так ка
