Основы молекулярной физики и термодинамики 2 страница

Wк=N<Wвр>=NkТ.

Число молекул определяется соотношением:

где m– молекулярная масса кислорода;

m – его масса;

N_А – число Авогадро.

Таким образом:

Подставив численные значения, предварительно выразив их в системе СИ, будем иметь:

<Wвр>=1,38×10^–23×350=4,83×10^–21 Дж.

Дж.

Ответ: W_к=364 Дж.

16. Масса 10 г кислорода находится при давлении 304 кПа и температуре 10 ^oС. После расширения вследствие нагревания при постоянном давлении кислород занял объем 10 л. Найти объем газа до расширения, температуру газа после расширения, плотности газа до и после расширения.

Решение. Согласно условию задачи, расширение газа вследствие нагревания происходило при постоянном давлении. В этом случае оказывается справедливым соотношение

.

Для определения температуры газа после расширения воспользуемся уравнением Менделеева-Клапейрона для конечного состояния газа

,

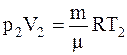где p₂ – давление газа после расширения;

V₂ – его объем после расширения;

m – масса газа;

m – молекулярная масса кислорода;

R – универсальная газовая постоянная;

T₂ – абсолютная температура газа.

Следовательно, для конечной температуры имеем

Для определения объема газа до расширения можно вновь воспользоваться уравнением Менделеева-Клапейрона, записанным для первоначального состояния газа:

где p₁, V₁, T₁ – его давление, объем и температура до расширения.

Из данного уравнения имеем

.

Учитывая то, что плотность газа r₁=m/V₁, подставляя значения V₁ и V₂ из уравнений Менделеева-Клапейрона, записанные для соответствующих состояний, для плотности кислорода до и после расширения будем иметь

и

Подставляя численные значения в системе СИ, окончательно имеем

;

л;

r₁= 4,14 кг/м³;

r₂=1кг/м³.

Ответ: ; л; r₁= 4,14 кг/м³; r₂=1кг/м³.

17. Масса газа 12 г занимает объем 4 л при температуре 7 ^oC После нагревания газа при постоянном давлении его плотность стала равной 0,6 кг/м³. До какой температуры нагрели газ?

Решение. Воспользовавшись уравнением Менделеева-Клапей-рона

можно показать, что между плотностью газа r=m/V и давлением существует связь

Следовательно, в начальном состоянии давление газа

В конечном

Так как нагревание газа производилось при постоянном давлении, то p₁=p₂

отсюда

Подставляя численные значения в системе СИ для конечной температуры, будем иметь:

Ответ: T₂=1400 K.

18. В баллоне находилась масса m₁=10 кг газа при давлении p₁=10 МПа. Какую массу газа взяли из баллона, если давление стало равным p₂=2,5 МПа? Температуру газа считать постоянной.

Решение. Запишем уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) для двух состояний: начального и конечного

и

Из второго соотношения определяем объем сосуда и подставляем его значение в первое уравнение, имеем:

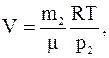а

Из последнего соотношения получаем связь между давлением газа в сосуде и его массой для данного случая:

Отсюда масса газа оставшегося в баллоне:

.

Так как масса израсходованного газа Dm=m₁–m₂, то окончательно, после соответствующих преобразований, имеем

Подставляя численные значения (в системе СИ) определяем массу взятого из баллона газа:

кг.

Ответ: Δm=7,5 кг.

19. В сосуде находится масса m₁=14 г азота и масса m₂=9 г водорода при температуре 10 ^oС и давлении 1 МПа. Найти молярную массу смеси и объем сосуда.

Решение. По закону Дальтона давление смеси газов равно сумме парциальных давлений компонентов входящих в смесь

p=p₁+p₂,

где p – давление смеси;

p₁ – парциальное давление азота;

p₂ – парциальное давление водорода.

Из уравнения Менделеева-Клапейрона:

Для каждого из давлений (смеси и парциальных) можно записать:

;

;

.

Следовательно, так как p=p₁+p₂, имеем:

.

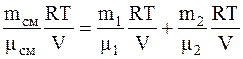Откуда

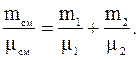
Из последнего соотношения для молекулярной массы смеси будем иметь:

Из уравнения Менделеева-Клапейрона, для смеси газов, объем сосуда равен:

Подставляя численные значения в системе СИ, находим молекулярную массу смеси:

кг/кмоль.

и объем сосуда

м³.

Ответ: μ_см=4,6 кг/кмоль; V=11,7×10^{-3 м3}.

20. Для получения хорошего вакуума в стеклянном сосуде, для удаления адсорбированного газа, необходимо прогревать стенки сосуда при откачке. На сколько может повыситься давление в сферическом сосуде радиусом 10 см, если адсорбированные молекулы перейдут со стенок в сосуд? Площадь поперечного сечения молекул S_o=10^–19 м². Температура газа в сосуде 300 ^oС. Слой молекул на стенках считать мономолекулярным.

Решение. Для определения давления воспользуемся основным уравнением молекулярно–кинетической теории в виде

p=n_okT,

где n_o – число молекул в единице объема;

k – постоянная Больцмана;

Т – абсолютная температура газа.

С учетом того, что

n_o=N/V,

где N – число молекул в объеме V, для давления имеем

По условию задачи слой молекул в сосуде мономолекулярный, следовательно, число молекул в нем можно определить исходя из соображений:

,

где S=4pr² – площадь поверхности сосуда;

S_o – площадь поперечного сечения молекул газа.

Так как сосуд сферический, то его объем V=4/3pr³.

Таким образом, окончательно для давления газа в сосуде будем иметь соотношение:

Подставляя численные значения в полученное соотношение (в системе СИ) определяем давление газа в сосуде

Па.

Ответ: p=2,4 Па.

21. В воздухе содержится 23,6% кислорода и 76,4% азота (по массе) при давлении 100 кПа и температуре 13 ^oС. Найти плотность воздуха и парциальные давления кислорода и азота.

Решение. Для определения плотности воздуха воспользуемся уравнениемМенделеева-Клапейрона

откуда

а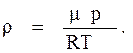

Для определения парциальных давлений так же воспользуемся уравнением Менделеева-Клапейрона, записанным для каждого из компонентов, входящих в смесь воздуха:

где V – объем воздуха.

Откуда

Так как r=m/V, то V=m/r, следовательно

Подставляя численные значения в системе СИ, для плотности воздуха и парциальных давлений кислорода и азота будем иметь:

кг/м³;

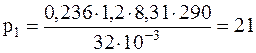кПа;

кПа.

Ответ: ρ=1,2 кг/м³; p₁=21 кПа; p₂=79 кПа.

22. В сосуде находится количество n=10^–7 моль кислорода и масса m₂=10^{–6 г азота. Температура смеси 100 o}С, давление в сосуде p=133 мПа. Найти объем сосуда, парциальные давления кислорода и азота и число молекул в единице объема.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, записанным для смеси газов в виде

,

где n_см=n₁+n₁=(n₁+m₂/m₂) – число молей или киломолей газов составляющих смесь.

Имеем

pV=(n₁+m₂/m₂)RT.

Отсюда

V=(n₁+m₂/m₂)(RT/p).

Парциальные давления компонентов образующих смесь определяем так же из уравнения Менделеева-Клапейрона, записанным для каждого из газов

p₁V=n₁RT и p₂V=(m₂/m₂)RT.

Откуда для парциальных давлений кислорода и азота соответственно имеем

p₁=n₁RT/V и p₂=m₂RT/m₂V.

Для определения числа молекул в единице объема необходимо воспользоваться основным уравнением молекулярно – кинетической теории для давления

p=n_okT.

Из него

n_o=p/kT.

Подставляя в ранее полученные формулы ы системе СИ для объема, парциальных давлений кислорода и азота и числа молекул в единице объема, имеем:

м³;

мПа;

мПа;

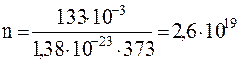м^-3.

Ответ: V=3,2·10^-3 м³; p₁=98 мПа; p₂=35 мПа; n=2,6·10¹⁹ м^-3.

23. Один моль идеального 2–х атомного газа, занимает объем 12,3 л под давлением 2 ат. нагревается при постоянном объеме до давления 3 ат. Далее газ расширяется при постоянном давлении до объема 24,6 литра, после чего охлаждается при постоянном объеме до начального давления, и наконец, сжимается при постоянном давлении до начального объема. Определить температуру газа для характерных точек цикла (рис. 3.8).

Решение. Пусть V' – наименьший объем газа;

V" – наибольший объем газа;

p'– наименьшее давление газа;

p" – наибольшее давление газа;

T₁, T₂, T₃, T₄ – температуры газа в характерных точках.

Температуру T₁ можно определить используя уравнение Менделеева-Клапейрона, записанном в виде:

.

Откуда

Переход газа из состояния 1 в состояние 2 – изохорный, для которого справедливо соотношение:

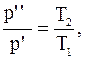
Следовательно,

Переход газа из состояния 2 в состояние 3 – изобарный, для которого справедливо соотношение:

.

Откуда

Переход газа из состояния 3 в состояние 4 – изохорный, для которого справедливо соотношение

следовательно,

Подставляя численные значения из условия задачи, будем иметь:

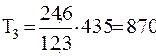К;

К;

К;

К.

Ответ: T₁=290 К; T₂=435 К; T₃=870 К; T₄=580 К.

24. Плотность смеси азота и водорода при температуре 47 ^oС и давлении p=2,00 ат равна=0,30 г/л. Найти концентрации молекул азота (n₁) и водорода (n₂) в смеси.

Решение. Концентрацию однородного по составу газа можно найти из формулы

p=n_okT.

В условии задачи дана смесь двух газов, молекулы которых различаются по массе. Приведенная формула является следствием основного уравнения кинетической теории газов

p=(2/3)n_o<W_к>,

где n_o – число молекул в единице объема (концентрация молекул);

<W_к>=<mv²>/2 – средняя кинетическая энергия поступательного движения одной молекулы газа. Для однородных по составу частиц газа <W_к>=mv²/2.

Из основного уравнения кинетической теории газов вытекает, что оно справедливо для совокупности любых частиц, в том числе различных по массе. Следовательно, формулу p=n_okT можно применять для смеси газов. В этом случае n_o – полное число частиц в единице объема. Таким образом, имеем

n_o=p/kT.

Для определения концентрации азота и водорода кроме очевидного соотношения

n₁+n₂=n_o=p/kT

необходимо иметь еще одно уравнение, связывающее величины n₁ и n₂.

Используя данные задачи, можно найти молярную массу смеси рассматриваемых газов (m_см), пользуясь уравнением Менделеева-Клапейрона

pV=mRT/m_см или p=rRT/m_см.

Откуда

m_см=rRT/p.

С другой стороны, можно выразить m_см через молярные массы азота (m₁) и водорода (m₂), а также их концентрации n₁ и n₂, записав уравнение газового состояния для каждого из газов входящих в смесь

pV=m×RT/m_см,
p₁V=m₁RT/m₁,
p₂V=m₂RT/m₂.

Откуда

p=m×RT/(m_cмV),
p₁=m₁RT/(m₁V),
p₂=m₂RT/(m₂V).

На основании закона Дальтона, давление смеси газов равно сумме парциальных давлений

p=p₁+p₂.

Имеем

p=m₁RT/ m₁V+m₂RT/m₂V=(m₁/m₁+m₂/m₂)RT/V,

где (m₁/m₁+m₂/m₂)=(m₁+m₂)/m_см.

Для молярной массы смеси азота и водорода получаем

m_см=m₁m₂(m₁+m₂)/(m₁m₂+m₂m₁).

Заметим также, что между массой m газа и его концентрацией n существует связь:

m=nVm'=nVm/N_А,

где V – объем газа;

m – его молярная масса;

m' – масса одной молекулы;

N_А – число Авогадро.

С учетом последнего соотношения, для молярной массы смеси имеем:

m_см=(m₁n₁+m₂n₂)/(n₁+n₂).

Решив систему уравнений, найдем неизвестные n₁ и n₂:

n₁=(rRT-pm₂)/(kT(m₁-m₂)),
n₂₌(rRT-pm₁)/(kT(m₂-m₁)).

Выражая входящие в формулы величины в единицах СИ, подставив их значения, выполнив вычисления, получим

n₁=3,57×10²⁴ м^-3; n₂=4,1×10²⁵ м^-3.

Ответ: n₁=3,57×10²⁴ м^-3; n₂=4,1×10²⁵ м^-3.

25. Средняя квадратичная скорость молекул некоторого газа 450 м/с. Давление газа 50 кПа. Найти плотность газа при этих условиях.

Решение. Средняя квадратичная скорость молекул газа связана с его температурой соотношением

,

где R – универсальная газовая постоянная;

μ – молекулярная масса газа;

T – абсолютная температура газа.

Для определения температуры газа воспользуемся уравнением Менделеева-Клапейрона

,

где r=m/V – плотность газа.

Следовательно,

.

Откуда

Подставляя численные значения, имеем:

кг/м³.

Ответ: ρ=0,74 кг/м³.

26. Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Эффективный диаметр молекул воздуха s=0,3 нм.

Решение. Средняя длина свободного пробега молекул газа

,

где <v> – средняя арифметическая скорость молекул;

<z> – среднее число столкновений каждой молекулы с остальными молекулами в единицу времени;

σ – эффективный диаметр молекулы;

n – число молекул в единице объема (концентрация молекул). Для определения числа молекул в единице объема воспользуемся основным уравнением молекулярно–кинетической теории для давления

p=nkT,

,

где k – постоянная Больцмана;

Т – температура газа.

Тогда для средней длины свободного пробега имеем

.

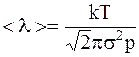Подставляя численные значения, окончательно получаем:

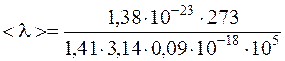=93×10^-9 м=93 нм.

Ответ: <λ>=93 нм.

27. Найти среднее число столкновений в единицу времени молекул углекислого газа при температуре 100 ^oС, если средняя длина свободного пробега <l>=870 мкм.

Решение. Число столкновений молекул газа в единицу времени связано со средней длиной свободного пробега соотношением

,

где – средняя арифметическая скорость.

Следовательно,

.

Подставляя численные значения, имеем

с^-1.

Ответ: <z>=4,9×10⁵ с^-1.

28. При некотором давлении и температуре 0 ^oС средняя длина свободного пробега молекул кислорода 95 нм. Найти среднее число столкновений в единицу времени молекул кислорода, если давление кислорода уменьшить в 100 раз.

Решение. Среднее число столкновений в единицу времени

где – средняя арифметическая скорость молекул газа;

<l> – средняя длина свободного пробега молекул.

При изменении давления газа длины свободного пробега обратно пропорциональны давлению:

где l₁, l₂ – длина свободного пробега молекул газа при соответствующих давлениях p₁ и p₂.

В нашем случае:

.

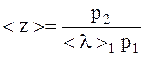
Подставляя численные значения для <z>, имеем

.

Ответ: <z>=4,5×10⁷ с^-1.

29. Какая часть молекул кислорода при t= 0 ^oС обладает скоростями от 100 до 110 м/с?

Решение. Согласно распределению молекул по скоростям (закону Максвелла)

,

где u=v/v_в – относительная скорость;

v – данная скорость;

– наиболее вероятная скорость молекул;

Du – интервал относительных скоростей, малый по сравнению со скоростью u.

Тогда искомая часть молекул, которую необходимо определить

.

В нашем случае v=100 м/с; Δv=10 м/с; наиболее вероятная скорость v=(2RT/pm)^1/2=376 м/с. Следовательно, u=v/v_в=100/376, u²=0,071; Du=10/376; exp(–u²)=0,93.

Тогда

Ответ:ΔN/N=0,4%.

30. Сосуд, содержащий газ, движется со скоростью v_o, затем быстро останавливается. На сколько увеличится при этом средний квадрат скорости теплового движения молекул газа в случаях: одноатомного газа, двухатомного газа? Газ считать идеальным.

Решение. Воспользуемся законом сохранения энергии. Пусть M масса газа в сосуде. Двигаясь со скоростью v газ, как целое, обладает кинетической энергией

.

Эта формула определяет кинетическую энергию направленного движения молекул, в котором они участвуют вместе с сосудом. После остановки сосуда направленное движение молекул в результате их соударений со стенками сосуда очень скоро превратится в хаотическое.

Пренебрегая теплообменом между газом и стенками сосуда за рассматриваемый промежуток времени, можно газ считать изолированной системой. Тогда из закона сохранения энергии следует, что «исчезнувшая» кинетическая энергия направленного движения молекул W должна быть равна приросту энергии хаотического движений молекул (приросту внутренней энергии DU):

W_к=DU.

Определим внутреннюю энергию газа. Для идеального одноатомного газа это есть энергия поступательного хаотического движения молекул:

,

где m – масса молекулы;

N – число молекул в сосуде.

Имеем

Отсюда следует, что изменение внутренней энергии одноатомного газа при торможении

DU=U₂-U₁= 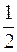M[v²_кв2-v²_кв1],

где v_кв1,v_кв2 – средние квадратичные скорости молекул газа соответственно в начале и конце торможения.

Подставив в уравнение W_к=DU значения W_к и DU, получим первый ответ

v²_кв2–v²_кв1=v₀².

Внутренняя энергия идеального двухатомного газа складывается из энергий поступательного и вращательного движения молекул. При этом три степени свободы приходятся на поступательное движение и две – на вращательное. В соответствии с законом о равномерном распределении энергии по степеням свободы, три пятых кинетической энергии W пойдет на увеличение энергии поступательного движения молекул и две пятых – на увеличение энергии их вращательного движения. Таким образом, имеем:

.

Из последнего соотношения получим второй ответ:

.

Ответ: 1) ; .