2.1.01. Тело массой 100 г, брошенное вертикально вниз с высоты 20 м со скоростью 10м/с, упало на Землю со скоростью 20 м/с. Найти работу по преодолению сопротивления воздуха (g=9,8 м/с2).
Ответ: а) A=4 Дж; б) A=4,9 Дж; в) A=9,8 Дж; г) A=4,6 Дж;
д) A=2,3 Дж.
2.1.02.1. Вычислить работу, совершаемую на пути 12 м, равномерно возрастающей силой, если в начале пути сила равна 10 Н, в конце пути 46 Н.
Ответ: а) А=3 Дж; б) А=33 Дж; в) А=36 Дж; г) А=336 Дж;
д) А=6 Дж.
2.1.03. Во сколько раз работа двигателя автомобиля по увеличению его скорости от 36 км/ч до 72 км/ч больше работы двигателя того же автомобиля, совершаемой для разгона его с места до скорости 36 км/ч? Силу сопротивления считать постоянной.
Ответ: а) A1/A2=2; б) A1/A2=4; в) A1/A2=6; г) A1/A2=5;
д) A1/A2=3.
2.1.04. Обруч (рис. 2.22) массой 1 кг и диаметром 0,6 м вращается вокруг оси, проходящей через центр, делая 20 об/с. Какую работу необходимо совершить, чтобы остановить обруч?
Ответ: а) А=71 Дж; б) А=710 Дж; в) А=7,1 Дж; г) А=0,710 Дж; д) А=0,071 Дж.
2.1.05. Медный шар радиусом R=0,1 м вращается с угловой скоростью 2 с-1 вокруг оси, проходящей через его центр (рис. 2.23). Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое? Плотность меди r=8,6∙103 кг/м3.
Ответ: а) А=8,64 Дж; б) А=86,4∙10-2 Дж; в) А=86,4 Дж;
г) А=864 Дж; д) А=0,0864 Дж.
2.1.06. Какую минимальную работу надо совершить, чтобы однородный куб массой m=100 кг и длиной ребра l=50 см, находящийся на горизонтальной плоскости (рис. 2.24), перевернуть с одной грани на соседнюю?
Ответ: а) А=90 Дж; б) А=92 Дж; в) А=94 Дж; г) А=96 Дж; д) А=98 Дж.
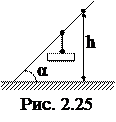2.1.07. По наклонной канатной дороге, составляющей с горизонтом угол α=450, поднимается вагонетка массой 500 кг (рис. 2.25). Какую минимальную работу совершает мотор подъемника при поднятии вагонетки на высоту h=10 м? Коэффициент трения равен μ=0,1.
Ответ: а) А=60 кДж; б) А=58 кДж; в) А= =56 кДж; г) А=54 кДж; д) А=52 кДж.
2.1.08. Какую работу совершает человек, поднимающий груз массой 2,0 кг на высоту 1,5 м с ускорением 3,0 м/с2?
Ответ: а) А=42,4 Дж; б) А=40,4 Дж; в) А=38,4 Дж; г) А= =36,4 Дж; д) А=34,4 Дж.
2.1.09. Лифт массой 1 т равноускоренно поднимается лебедкой. На некотором отрезке пути длиной 1,0 м лифт двигался со средней скоростью 5,0 м/с и его скорость возросла на 0,5 м/с. Какую работу совершила лебедка на указанном отрезке пути?
Ответ: а) А=11,3 кДж; б) А=12,3 кДж; в) А=13,3 кДж; г) А= =14,3 кДж; д) А=15,3 кДж.
2.1.10. Какую работу нужно совершить при сжатии пружины детского пистолета на Δℓ=3,0 см (рис. 2.26), если усилие составляет 20,0 Н? Какова потенциальная энергия сжатой пружины?
Ответ: а) А=0,3 Дж; б) А=0,5 Дж; в) А=0,7 Дж; г) А=0,9 Дж; д) А=1,1 Дж.
2.1.11. Динамометр, рассчитанный на 40,0 Н, имеет пружину с жесткостью 0,5 кН/м. Какую работу надо совершить, чтобы растянуть пружину от середины шкалы до последнего деления?
Ответ: а) А=1,2 Дж; б) А=1,4 Дж; в) А=1,6 Дж; г) А=1,8 Дж; д) А=2,0 Дж.
2.1.12. Камень массой 0,5 кг, падая с высоты 10,0 м, имел у поверхности Земли в момент падения скорость 12,0 м/с. Определить силу сопротивления воздуха, считая ее постоянной.
Ответ: а) Fс=1,1 Н; б) Fс=1,3 Н; в) Fс=1,5 Н; г) Fс=1,7 Н;
д) Fс=1,9 Н.
2.1.13. Автомобиль на некотором отрезке пути увеличил свою скорость от 0 до 36 км/ч. На другом отрезке пути он увеличил свою скорость от 36 до 72 км/ч. Найти отношение работ, затраченных двигателем на разгон на втором и первом отрезках пути.
Ответ: а) A2/A1=3,4; б) A2/A1=3,2; в) A2/A1=3,0; г) A2/A1=2,8;
д) A2/A1=2,6.
2.1.14. Какую работу совершает постоянная сила, модуль которой равен 0,5 Н, действующая на тело массой 10 кг, в течение 2,0с? В начальный момент времени тело, движущееся равноускоренно, имело скорость 0,4 м/с.
Ответ: а) А=0,025 Дж; б) А=0,035 Дж; в) А=0,065 Дж;
г) А=0,045 Дж; д) А=0,055 Дж.
2.1.15. Орудие, масса ствола которого 450 кг стреляет в горизонтальном направлении. Масса снаряда 5 кг и начальная скорость его v=450 м/с. При выстреле ствол откатывается на 45 см. Определить среднее значение силы торможения, развивающейся в противооткатном устройстве орудия.
Ответ: а) <F>=16,5 кН; б) <F>=15,5 кН; в) <F>=14,5 кН;
г) <F>=13,5 кН; д) <F>=12,5 кН.
2.1.16. Пуля, вылетевшая из винтовки с начальной скоростью 1000 м/с, упала на Землю со скоростью 500 м/с. Какая работа была затрачена во время полета пули на преодоление силы сопротивления воздуха, если масса пули 10 г?
Ответ: а) А=3,35 кДж; б) А=3,45 кДж; в) А=3,55 кДж; г) А= =3,65 кДж; д) А=3,75 кДж.
2.1.17. Камень, пущенный горизонтально по поверхности льда со скоростью 2,0 м/с, прошел до полной остановки 20 м. Определить коэффициент трения камня по льду, считая его постоянным.
Ответ: а) m=0,06; б) m=0,05; в) m=0,03; г) m=0,01; д) m=0,001.
2.1.18. Пуля, масса которой 10 г, подлетает к доске толщиной 4,0 см и застревает в ней, почти пробив ее (рис. 2.27). Скорость пули перед взаимодействием с доской 600 м/с. Чему равна средняя сила сопротивления доски движению пули?
Ответ: а) F=25 кН; б) F=35 кН; в) F=45 кН; г) F=55 кН;
д) F=65 кН.
2.1.19. Какую работу надо совершить для того, чтобы равномерно передвинуть диван на 5 м по горизонтальному полу, нажимая на него руками под углом 300 к горизонту? Масса дивана 50 кг, а коэффициент трения дивана о пол 0,25.
Ответ: а) А=710 Дж; б) А=720 Дж; в) А=730 Дж; г) А=740 Дж; д) А=750 Дж.
2.1.20. Какой путь пройдут санки по горизонтальной поверхности после спуска с горы высотой 15 м, имеющий уклон 300 (рис. 2.28)? Коэффициент трения считать постоянным во время всего движения и равным μ=0,025.
Ответ: а) S=570 м; б) S=560 м; в) S=550 м; г) S=540 м;
д) S=530 м.
2.1.21. Кольцо массой 5 кг катится по горизонтальной поверхности со скоростью 54 км/ч. Найти его кинетическую энергию Wк.
Ответ: а) Wк=562,5 Дж; б) Wк=1125 Дж; в) Wк=7290 Дж;
г) Wк=14,58 кДж; д) Wк=762,5 Дж.
2.1.22. Обруч, имеющий массу 2 кг, катится без скольжения со скоростью 5 м/с. Найти кинетическую энергию этого тела.
Ответ: а) Wк=50 Дж; б) Wк=40 Дж; в) Wк=30 Дж; г) Wк=20 Дж; д) Wк=10 Дж.
2.1.23. Сплошной цилиндр, имеющий массу 2кг, катится без скольжения со скоростью 5 м/с. Найти кинетическую энергию этого цилиндра.
Ответ: а) Wk=37,5 Дж; б) Wk=35,5 Дж; в) Wk=33,5 Дж;
г) Wk= =31,5 Дж; д) Wk=29,5 Дж.
2.1.24. Пуля массой 10 г летит со скоростью 800 м/с, вращаясь около продольной оси с частотой 3000 об/с. Принимая пулю за цилиндр диаметром 8 мм, определить полную кинетическую энергию пули.
Ответ: а) Wк=2×103 Дж; б) 3×103 Дж; в) 1×103 Дж; г) 2,3×103 Дж; д) Wк=3,2×103 Дж.
2.1.25. Определить значение полной механической энергии колеблющейся материальной точки массой 25 г. Амплитуда колебаний равна 10 см, период-0,5 с.
Ответ: а) W=1,97 Дж; б) W=1,97×10-2 кДж; в) W=1,97 кДж;
г) W=1,97×10-2 Дж; д) W=0,97×10-2 Дж.
2.1.26. Определить значение кинетической энергии колеблющейся материальной точки массой 25 г для того момента, когда смещение равно 6 см. Амплитуда колебаний равна 10 см, период – 0,5 с.
Ответ: а) Wk=19,7 мДж; б) Wk=18,7 мДж; в) Wk=17,7 мДж;
г) Wk=16,7 мДж; д) Wk=15,7 мДж.
2.1.27. Частица массой m=0,01 кг совершает гармонические колебания с периодом T=2 с. Полная энергия колеблющейся частицы W=0,1 мДж. Определить амплитуду А колебаний частицы.
Ответ: а) А=55 мм; б) А=65 мм; в) А=35 мм; г) А=25 мм;
д) А=45 мм.
2.1.28. Висящий на невесомой пружине груз совершает вертикальные колебания с амплитудой 4 см. Определите полную энергию гармонических колебаний, если для упругого удлинения пружины на 1 см требуется сила 1 Н.
Ответ: а) W=0,02 Дж; б) W=0,04 Дж; в) W=0,08 Дж; г) W= =016 Дж; д) W=0,2 Дж.
2.1.29. Определить значение полной механической энергии колеблющейся материальной точки массой 25 г. Амплитуда колебаний равна 10 см, период – 0,5 с.
Ответ: а) W=1,97 Дж; б) W=1,97×10-2 кДж; в) W=1,97 кДж;
г) W=1,97×10-2 Дж; д) W=0,97×10-2 Дж.
2.1.30. Частица массой m=0,01 кг совершает гармонические колебания с периодом T=2 с. Полная энергия колеблющейся частицы W=0,1 мДж. Определить амплитуду А колебаний частицы.
Ответ: а) А=55 мм; б) А=65 мм; в) А=35 мм; г) А=25 мм;
д) А=45 мм.
2.1.31. Какова потенциальная энергия сжатой на 3,0 см пружины детского пистолета, если усилие составляет 20,0 Н?
Ответ: а) Wp=0,10 Дж; б) Wp=0,15 Дж; в) Wp=0,20 Дж;
г) Wp=0,25 Дж; д) Wp=0,30 Дж.
2.1.32. Мяч, масса и диаметр которого равны m=0,5 кг и d=0,24 м, погрузили в воду на глубину 4,0 м. На сколько изменилась его энергия? Деформацией мяча и поверхностным натяжением воды пренебречь. Плотность воды принять равной 1,0×103 кг/м3.
Ответ: а) DW=264,0 Дж; б) DW=260,0 Дж; в) DW=258,0 Дж; г) DW=256,0 Дж; д) DW=254,0 Дж.
2.1.33. При забивке сваи массой 150 кг использовалась энергия свободно падающего молота массой 50 кг. При этом свая погружалась в грунт на 10 см. С какой высоты должен падать молот, если сила сопротивления грунта постоянна и равна 6850 Н? Удар считать неупругим.
Ответ: а) h=4,0 м; б) h=4 м; в) h=4,2 м; г) h=4,4 м; д) h=4,6 м.
2.1.34. Вагон массой 20 т, двигаясь со скоростью 0,5 м/с, ударяется в два неподвижных пружинных буфера. Найти максимальной сжатие буферов, если известно, что при действии на каждый буфер силы 50,0 кН/м он сжимается на 1,0 см.
Ответ: а) Dl=1,8×10-2 м; б) Dl=2,0×10-2 м; в) Dl=2,2×10-2 м;
г) Dl=2,4×10-2 м; д) Dl=2,6×10-2 м.
2.1.35. К пружине, жесткость которой равна 1,0 кН/м, подвешен груз массой 3 кг и отпущен из состояния покоя. На какое расстояние опустится груз?
Ответ: а) Dl=5,3×10-2 м; б) Dl=5,5×10-2 м; в) Dl=5,7×10-2 м;
г) Dl=5,9×10-2 м; д) Dl=6,1×10-2 м.
2.1.36. Тело брошено вертикально вверх со скоростью 49 м/с. На какой высоте его кинетическая энергия будет равна потенциальной? Сопротивление воздуха не учитывать.
Ответ: а) h=69 м; б) h=67 м; в) h=65 м; г) h=63 м; д) h=61 м.
2.1.37. Мальчик, стреляя из рогатки, натянул резиновый шнур так, что его длина стала больше на 10 см. Определить энергию растянутого резинового шнура, если для растяжения шнура мальчик приложил силу 9,8 Н.
Ответ: а) W=0,58 Дж; б) W=0,68 Дж; в) W=0,78 Дж; г) W= =0,88 Дж; д) W=0,98 Дж.
2.1.38. Во сколько раз кинетическая энергия Wk искусственного спутника Земли, движущегося по круговой орбите, меньше его потенциальной энергии Wp в поле тяжести Земли?
Ответ: а) Wp/Wk=5; б) Wp/Wk=4; в) Wp/Wk=3; г) Wp/Wk=2;
д) Wp/Wk=1.
2.1.39. Обруч и диск одинаковой массы m1=m2 катятся без скольжения с одной и той же скоростью v. Кинетическая энергия обруча Wk1=39,2 Дж. Найти кинетическую энергию Wk2 диска.
Ответ: а) Wk2=26,4 Дж; б) Wk2=27,4 Дж; в) Wk2=28,4 Дж;
г) Wk2=29,4 Дж; д) Wk2=30,4 Дж.
2.1.40. Шар диаметром d=6 см и массой m=0,25 кг катится без скольжения по горизонтальной плоскости. Частота вращения шара n=2 об/с. Найти кинетическую энергию шара.
Ответ: а) Wk=0,06 Дж; б) Wk=0,08 Дж; в) Wk=0,1 Дж; г) Wk= =0,12 Дж; д) Wk=0,14 Дж.
2.1.41. Маховик вращается по закону, выраженному уравнением: j=2+16t-2t2.1. Момент инерции маховика 50 кг×м2.1. Чему равна мощность маховика в момент времени t=3 с?
Ответ: а) N=900 Вт; б) N=700 Вт; в) N=800 Вт; г) N=600 Вт; д) N=500 Вт.
2.1.42. Электровоз при движении со скоростью v=72 км/ч потребляет мощность Nз=600 кВт. Определить силу тяги электровоза, если его коэффициент полезного действия (КПД) равен 80%.
Ответ: а) F=30 кН; б) F=28 кН; в) F=26 кН; г) F=24 кН;
д) F=22 кН.
2.1.43. Тяговая мощность (мощность на крюке) трактора равна 30,0 кВт. С какой средней скоростью может тянуть этот трактор груженый прицеп массой 5,0 т на подъем 0,2 при коэффициенте сопротивления 0,4?
Ответ: а) v=1,4 м/с; б) v=1,2 м/с; в) v=1,0 м/с; г) v=0,8 м/с;
д) v=0,6 м/с.
2.1.44. Моторы электровоза при движении со средней скоростью 20,0 м/с потребляют мощность 8,0×105 Вт. Какова сила тяги мотора, если коэффициент полезного действия силовой установки электровоза 80%?
Ответ: а) F=30 кН; б) F=32 кН; в) F=34 кН; г) F=36 кН;
д) F=38 кН.
2.1.45. Поезд, отходя от станции, за 5 мин развивает скорость до 18 м/с. Масса поезда 6,0×105 кг, коэффициент трения 0,004. Определить среднюю мощность локомотива за время ускоренного движения.
Ответ: а) <N>=53,5×104 Вт; б) <N>=54,5×104 Вт; в) <N>= =55,5×104 Вт; г) <N>=56,5×104 Вт; д) <N>=57,5×104 Вт.
2.1.46. Поезд, отходя от станции, за 5 мин развивает скорость до 18 м/с. Масса поезда 6,0×105 кг, коэффициент трения 0,004. Найти минимальную мощность локомотива, при которой за указанное время состав наберет указанную скорость.
Ответ: а) Nmin=109,0×104 Вт; б) Nmin=107,0×104 Вт; в) Nmin= =105,0×104 Вт; г) Nmin=103,0×104 Вт; д) Nmin=101,0×104 Вт.
2.1.47. Камень шлифовального станка имеет диаметр 60 см и делает 120 об/мин. Обрабатываемая деталь прижимается к камню с силой 1000 Н. Какая мощность затрачивается на шлифовку, если коэффициент трения камня о деталь равен 0,2?
Ответ: а) N=1,3 кВт; б) N=1,4 кВт; в) N=1,5 кВт; г) N=1,6 кВт; д) N=1,7 кВт.
2.1.48. Двигатель автомобиля, движущегося равномерно по горизонтальной дороге, развивает мощность 62 кВт. Результирующая всех сил, действующих на автомобиль, в процессе его движения равна F=31 кН. Определить скорость автомобиля.
Ответ: а) v=78 км/ч; б) v=76 км/ч; в) v=74 км/ч; г) v=72 км/ч; д) v=70 км/ч.
2.1.49. Якорь электрического двигателя вращается с угловой скоростью w=1500 об/мин. Определить вращающий момент, если двигатель развивает мощность N=500 Вт.
Ответ: а) M=3,58 Н×м; б) M=3,48 Н×м; в) M=3,38 Н×м; г) M= =3,28 Н×м; д) M=3,18 Н×м.
2.1.50. Маховик вращается по закону, выражаемому уравнением j=2+32t-4t2.1. Найти среднюю мощность <N>, развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции I=100 кг×м2.1.
Ответ: а) <N>=16,8 кВт; б) <N>=15,8 кВт; в) <N>=14,8 кВт; г) <N>=13,8 кВт; д) <N>=12,8 кВт.
2.1.51. Шар скатывается с наклонной плоскости высотой 90 см (рис. 2.29.). Определить линейную скорость центра шара в тот момент, когда шар скатится с наклонной плоскости? Принять g=10 м/с2.1.
Ответ: а) v=3,55 м/с; б) v=35,5 м/с; в) v=3,55 см/с; г) v=0,355 м/с; д) v=3,55 см/с.
2.1.52. Из пружинного пистолета выстрелили пулькой, масса которой m=5 г. Жесткость пружины k=1,25 кН/м. Пружина была сжата на Dl=8 см. Определить скорость пульки при вылете ее из пистолета.
Ответ: а) v=400 м/с; б) v=40 м/с; в) v=420 м/с; г) v= 40 см/с;
д) v=4 м/с.
2.1.53. Стальной шарик падает с высоты 1 м. На какую высоту он поднимется после удара, если коэффициент восстановления равен 0,8? Коэффициентом восстановления называется отношение скорости после удара к скорости до удара (рис. 2.30).
Ответ: а) h=0,64 м; б) h=0,54 м; в) h=0,44 м;
г) h=0,74 м; д) h=0,84 м.
2.1.54. Металлический шарик, падая с высоты 1 м на стальную плиту, отскакивает от нее на высоту 0,81 м. Найти коэффициент восстановления материала шарика (рис. 2.30).
Ответ: а) k=0,7; б) k=0,5; в) k=0,6; г) k=0,9; д) k=0,8.
2.1.55. Деревянным молотком, масса которого равна 0,5 кг, со скоростью 1 м/с ударяют о неподвижную стенку. Считая коэффициент восстановления при ударе равным 0,5, найти количество тепла, выделившегося при ударе. Коэффициентом восстановления называется отношение величины скорости тела после удара к ее величине до удара.
Ответ: а) Q=19 Дж; б) Q=1,9 Дж; в) Q=0,19 Дж; г) Q=29 Дж; д) Q=2,9 Дж.
2.1.56. Тело массой 2 кг движется со скоростью 3 м/с и нагоняет второе тело массой в 3 кг, движущееся со скоростью 1 м/с. Найти скорости тел после столкновения, если удар был неупругий. Тела движутся по одной прямой (рис. 2.31). Удар-центральный.
Ответ: а) u12=2,8 м/с; б) u12=1,8 м/с; в) u12=3,8 м/с; г) u12=0,8 м/с; д) u12=1 м/с.
2.1.57. Тело массой 2 кг движется со скоростью 3 м/с и нагоняет второе тело массой в 3 кг, движущееся со скоростью 1 м/с. Найти скорости тел после столкновения, если удар был упругий. Тела движутся по одной прямой (рис. 2.31). Удар-центральный.
Ответ: а) u1=0,6 м/с; u2=2,6 м/с; б) u1=0,6 м/с; u2=2,6 м/с;
в) u1=0,6 м/с; u2=2,6 м/с; г) u1=0,6 м/с; u2=2,6 м/с; д) u1=0,6 м/с; u2=2,6 м/с.
2.1.58. Тело массой 3 кг движется со скоростью 4 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, найти количество теплоты, выделившейся при ударе.
Ответ: а) Q=24 Дж; б) Q=6 Дж; в) Q=12 Дж; г) Q=0 Дж;
д) Q=16 Дж.
2.1.59. Два свинцовых шарика массами 50 г и 200 г висят на двух параллельных нитях длиной 75 см каждая. Шарики соприкасаются. Большой шар отвели в сторону так, что его нить заняла горизонтальное положение, и затем отпустили. На какую высоту поднимутся шарики после соударения? Удар считать абсолютно неупругим (рис. 2.32).
Ответ: а) h=0,60 м; б) h=0,75 м; в) h= =0,38 м; г) h=0,52 м; д) h=0,48 м.
2.1.60. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n1=14 мин-1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n2=25 мин-1. Масса человека 75 кг. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки.
Ответ: а) M=3,10×102 кг; б) M=21 кг; в) M=0,31×103 кг; г) M= =1,91×102 кг; д) M=210 кг.
2.1.61. Камень брошен под углом к горизонту со скоростью v0=20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте от горизонта скорость камня уменьшится вдвое (рис. 2.33).
Ответ: а) h=11,3 м; б) h=12,3 м; в) h=13,3 м;
г) h=14,3 м; д) h=15,3 м.
2.1.62. Определить величину кинетической энергии тела массой m=1 кг, брошенного горизонтально со скоростью v0=20 м/с в конце четвертой секунды его движения (рис. 2.34). Принять g=10 м/с2.
Ответ: а) Wk=1,6 кДж; б) Wk=1,4 кДж; в) Wk=1,2 кДж; г) Wk= =1 кДж; д) Wk=0,8 кДж.
2.1.63. Пуля массой 10 г, двигаясь со скоростью 800 м/с, попадает в доску толщиной 5 см и вылетает из нее со скоростью 100 м/с (рис. 2.35). Определить силу сопротивления доски, считая эту силу постоянной.
Ответ: а) Fс=65 кН; б) Fс=64 кН; в) Fс=63 кН; г) Fс=62 кН; д) Fс=61 кН.
2.1.64. Камень массой m=20 г, выпущенный вертикально вверх из рогатки, резиновый жгут которой был растянут на Dl=20см, поднялся на высоту h=40 м. Найти коэффициент упругости жгута. Сопротивление воздуха не учитывать.
Ответ: а) k=390 Н/м; б) k=392 Н/м; в) k=394 Н/м; г) k=396 Н/м; д) k=398 Н/м.
2.1.65. Вагон массой m=20,0 т движется с начальной скоростью v0=54 км/ч. Найти среднюю силу, действующую на вагон, если известно, что вагон останавливается в течение времени t=100 с.
Ответ: а) Fс=3,0 кН; б) Fс=3,5 кН; в) Fс=4,0 кН; г) Fс=4,5 кН; д) Fс=5,0 кН.
2.1.66. Вагон массой m=20,0 т движется с начальной скоростью v0=54 км/ч. Найти среднюю силу, действующую на вагон, если известно, что вагон останавливается в течение времени t=10 с.
Ответ: а) Fс=30 кН; б) Fс=28 кН; в) Fс=26 кН; г) Fс=24 кН;
д) Fс=22 кН.
2.1.67. Вагон массой m=20,0 т движется с начальной скоростью v0=54 км/ч. Найти среднюю силу, действующую на вагон, если известно, что вагон останавливается в течение времени t=1 с.
Ответ: а) Fс=400 кН; б) Fс=300 кН; в) Fс=200 кН; г) Fс=100 кН; д) Fс=50 кН.
2.1.68. Поезд массой m=500 т после прекращении тяги паровоза под действием силы трения Fтр=98 кН останавливается через время t=1 мин. С какой скоростью v0 шел поезд?
Ответ: а) v0=10,8 м/с; б) v0=11,8 м/с; в) v0=12,8 м/с; г) v0= =13,8 м/с; д) v0=14,8 м/с.
2.1.69. Вагон массой m=20,0 т движется равнозамедленно, имея начальную скорость v0=54 км/ч, ускорение а=0,300 м/с2.1. Какая сила торможения Fт действует на вагон?
Ответ: а) Fт=8,0 кН; б) Fт=7,0 кН; в) Fт=6,0 кН; г) Fт=5,0 кН; д) Fт=4,0 кН.
2.1.70. Вагон массой m=20,0 т движется равнозамедленно, имея начальную скорость v0=54 км/ч, ускорение а=0,300 м/с2.1. Через какое время t вагон остановится?
Ответ: а) t=30 с; б) t=40 с; в) t=50 с; г) t=60 с; д) t=70 с.
2.1.71. Вагон массой m=20,0 т движется равнозамедленно, имея начальную скорость v0=54 км/ч, ускорение а=0,300 м/с2.1. Какое расстояние S вагон пройдет до остановки?
Ответ: а) S=365; б) S=395; в) S=385; г) S=375 м; д) S=355.
2.1.72. С неподвижной лодки массой 50 кг на берег прыгает человек, масса которого 80 кг. Скорость человека 1,2 м/с. С какой скоростью начнет двигаться лодка?
Ответ: а) v=-1,6 м/с; б) v=-1,7 м/с; в) v=-1,8 м/с; г) v=-1,9 м/с; д) v=-2,0 м/с.
2.1.73. На пол с высоты 2 м свободно падает мяч массой 200 г и подпрыгивает на высоту полутора метров. Определить переданный полу импульс. Сопротивлением воздуха пренебречь.
Ответ: а) Dp=2,73 кг×м/с; б) Dp=2,63 кг×м/с; в) Dp=2,53 кг×м/с; г) Dp=2,43 кг×м/с; д) Dp=2,33 кг×м/с.
2.1.74. На пол с высоты 2 м свободно падает мяч массой 200 г и подпрыгивает на высоту 1,5 м. Определить количество энергии, перешедшей в немеханические формы, при не вполне упругом соударении с полом. Сопротивлением воздуха пренебречь.
Ответ: а) DW=0,941 Дж; б) DW=0,951 Дж; в) DW=0,961 Дж; г) DW=0,971 Дж; д) DW=0,981 Дж.
2.1.75. Тело с начальной скоростью v=14 м/с падает с высоты h=240 м и углубляется в песок на 0,2 м. Определить среднюю силу сопротивления почвы. Масса тела 1 кг. Сопротивление воздуха не учитывать.
Ответ: а) F=12,5 кН; б) F=13,5 кН; в) F=14,5 кН; г) F=15,5 кН; д) F=16,5 кН.
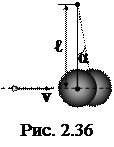2.1.76. Пуля, летящая горизонтально, попадает в шар, подвешенный на очень легком, жестком стержне, и застревает в нем (рис. 2.36). Масса пули в 103 раз меньше массы шара. Расстояние от точки подвеса до центра шара 1 м. Какова была скорость пули, если известно, что стержень с шаром отклонился в результате такого взаимодействия на угол 100?
Ответ: а) v=560 м/с; б) v=550 м/с; в) v=540 м/с; г) v=530 м/с; д) v=520 м/с.
2.1.77. Человек, бегущий со скоростью 8,1 км/ч, догоняет тележку, движущуюся со скоростью 2,9 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка, если ее масса 80 кг, а масса человека 60 кг?
Ответ: а) u=3,1 км/ч; б) u=4,1 км/ч; в) u=5,1 км/ч; г) u=6,1 км/ч; д) u=7,1 км/ч.
2.1.78. Конькобежец, масса которого 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8,0 м/с. На какое расстояние откатится конькобежец в результате отдачи, если известно, что коэффициент трения коньков о лед равен 0,02?
Ответ: а) x=0,6 м; б) x=0,5 м; в) x=0,4 м; г) x=0,3 м; д) x=0,2 м.
2.1.79. Мальчик, стреляя из рогатки, натянул резиновый шнур так, что его длина стала больше на 10 см. С какой скоростью полетел камень массой 20 г? Для растяжения шнура на 1 см нужно приложить силу 9,8 Н.
Ответ: а) v=26,2 м/с; б) v=25,2 м/с; в) v=24,2 м/с; г) v=23,2 м/с; д) v=22 м/с.
2.1.80. Обручу, радиус которого r=0,5 м, поставленному на шероховатую горизонтальную поверхность, сообщили в горизонтальном направлении поступательную скорость v0=2 м/с. Определить угловую скорость вращения обруча w после того, как проскальзывание обруча прекратилось.
Ответ: а) w=2 с-1; б) w=3 с-1; в) w=4 с-1; г) w=5 с-1; д) w=6 с-1.
2.1.81. Определить напряженность гравитационного поля на высоте 1000 км над поверхностью Земли (рис. 2.37). Считать известными ускорение свободного падения у поверхности Земли и ее радиус.
Ответ: а) g=8,33 м/с2; б) g=7,93 м/с2; в) g=7,33 м/с2; г) g=2 м/с2; д) g=3 м/с2.1.
2.1.82.1. Космическая ракета летит на Луну. На каком расстоянии от центра Земли находится точка, в которой ракета будет притягиваться Землей и Луной с одинаковой силой (рис. 2.38)? (Точка расположена на прямой, соединяющей центры Луны и Земли между ними). Расстояние от Земли до Луны принять равным 60 земным радиусам, массу Луны считать в 81 раз меньше массы Земли.
Ответ: а) x=Rз; б) x=5Rз; в) x=40Rз; г) x=4Rз; д) x=54Rз.
2.1.83. С какой скоростью движется Земля вокруг Солнца? Принять, что Земля движется по круговой орбите. (G=6,67∙10-11 Н∙м2/кг2; r=1,5∙1011 м; Мс=1,99∙1030 кг).
Ответ: а) v=9,8 км/с; б) v=8 км/с; в) v=9, км/с; г) v=19,8 км/с; д) v=29,8 км/с.
2.1.84. Определить линейную скорость спутника Земли, обращающегося по круговой орбите на высоте 1000 км. Ускорение свободного падения у поверхности Земли и ее радиус считать известными (рис. 2.39).
Ответ: а) v=73,6×103 м/с; б) v=0,0736×103 м/с;
в) v=7,36×103 м/с; г) v=736×103 м/с; д) v=0,736×103 м/с.
2.1.85. Определить угловую скорость спутника Земли, обращающегося по круговой орбите на высоте 1000 км. Ускорение свободного падения у поверхности Земли и ее радиус считать известными (рис. 2.39).
Ответ: а) ω=0,59×10-3 1/с; б) ω=0,69×10-3 1/с; в) ω=0,79×10-3 1/с; г) ω=0,89×10-3 1/с; д) ω=0,99×10-3 1/с.
2.1.86. Какова масса Земли, если считать, что Луна в течение года совершает 13 оборотов вокруг Земли и расстояние от Земли до Луны равно 3,84×108 м?
Ответ: а) Мз=5,77×1030; б) Мз=57,7×1024; в) Мз=0,577×1024;
г) Мз=0,587×1030; д) Мз=5,71×1024 кг.
2.1.87. Спутник обращается вокруг Земли по круговой орбите на высоте 520 км. Определить период обращения спутника. Ускорение свободного падения у поверхности Земли и ее радиус считать известными. (g=9,8 м/с2; Rз=6,4∙106 м).
Ответ: а) T=5,7×103 с; б) T=7×103 с; в) T=5×103 с; г) T=6×103 с;
д) T=10×103 с.
2.1.88. С какой линейной скоростью движутся точки земного экватора при вращении Земли вокруг своей оси? Радиус Земли 6380 км.
Ответ: а) v=464 м/с; б) v=454 м/с; в) v=444 м/с; г) v=434 м/с; д) v=424 м/с.
2.1.89. На какую высоту над поверхностью Земли нужно вывести искусственный спутник, чтобы он, двигаясь по круговой орбите, всегда находился над одной и той же точкой поверхности Земли? Период обращения спутника вокруг Земли принять равным 86,4×103 с.
Ответ: а) h=42×106 м; б) h=40×106 м; в); г) h=38×106 м;
д) h=36×106 м.
2.1.90. Искусственный спутник Луны движется по круговой орбите на расстоянии 100 км от поверхности Луны. Найти линейную скорость движения этого спутника.
Ответ: а) v=1,33×103 м/с; б) v=1,43×103 м/с; в) v=1,53×103 м/с;
г) v=1,63×103 м/с; д) v=1,73×103 м/с.
2.1.91. Искусственный спутник Луны движется по круговой орбите на расстоянии 100 км от поверхности Луны. Найти период обращения этого спутника.
Ответ: а) T=5,1×103 с; б) T=6,1×103 с; в) T=7,1×103 с; г) T= =8,1×103 с;д) T=9,1×103 с.
2.1.92. Определить центростремительное ускорение, которым обладает тело на экваторе Земли. Радиус Земли – 6400 км.
Ответ: а) aц=0,023 м/с2; б) aц=0,033 м/с2; в) aц=0,043 м/с2;
г) aц=0,053 м/с2; д) aц=0,063 м/с2.1.
2.1.93. Масса Луны составляет 1,2% массы Земли. Расстояние между их центрами 384000 км. Где расположен центр масс системы «Земля–Луна»?
Ответ: а) x=4600 км от центра Земли; б) x=4600 км от центра Луны; в) x=4900 км от центра Земли; г) x=4900 км от центра Луны; д) x=5600 км от центра Земли.
2.1.94. Средняя угловая скорость вращения Земли вокруг Солнца равна 10 в сутки. Расстояние Земли от Солнца 1,5×108 км. Определить массу Солнца.
Ответ: а) М=5×1030 км; б) М=4×1030 км; в) М=3×1030 км; г) М= =2×1030 км; д) М=1×1030 км.
2.1.95. Определить работу сил тяжести, совершаемую над искусственным спутником массы m, движущийся по круговой орбите радиуса R вокруг Земли со скоростью v, за один полный оборот.
Ответ: а) A=10 Дж; б) A=5 Дж; в) A=8 Дж; г) A=0 Дж;
д) A=4 Дж.
2.1.96. С поверхности Земли вертикально вверх запущена ракета со скоростью 5 км/с. На какую высоту она поднимется? Считать, что Mз=5,98∙1024 кг; G=6,67∙10-11 Н∙м2/кг2; Rз=6,4∙106 м.
Ответ: а) h=1,6×104 м; б) h=16×106 м; в) h=0,16×106 м; г) h= =1,6×1010 м; д) h=1,6×106 м.
2.1.97. Какую работу необходимо совершить, чтобы вывести на орбиту искусственной планеты солнечной системы тело массой m=500 кг?
Ответ: а) A=312×1010 Дж; б) A=31,2×1010 Дж; в) A=3,12×1010 Дж; г) A=3,12×108 Дж; д) A=0,312×1010 Дж.
2.1.98. Вычислить работу А12 сил гравитационного поля Земли при перемещении тела массой m=10 кг из точки 1 в точку 2.1. Радиус Земли и ускорение свободного падения вблизи поверхности Земли считать известными (рис. 2.40). Расстояние от точки 1 до поверхности Земли r1=2Rз, а от точки 2 r2=Rз.
Ответ: а) А12=104 МДж; б) А12=204 МДж; в) А12=84 МДж; г) А12=10 МДж; д) А12=150 МДж.
2.1.99. Определить работу, которую совершают силы гравитационного поля Земли, если тело массой 1 кг упадет на поверхность Земли с высоты, равной радиусу Земли.
Ответ: а) 20×106 Дж; б) 10×106 Дж; в) 21×106 Дж; г) 11×106 Дж; д) A=31×106 Дж.
2.1.100. С какой скоростью должна быть выброшена с поверхности Солнца частица, чтобы она могла удалиться в бесконечность?
Ответ: а) v=7,92 км/с; б) v=618 км/с; в) v=12 км/с; г) v=29,2 км/с; д) v=15 км/с.
2.1.101. Найти релятивистское сокращение размеров тела, скорость которого равна 95% скорости света.
Ответ: а) 51%; б) 31%; в) 41%; г) 21%; д) 11%.
2.1.102. Какую скорость v должно иметь движущееся тело, чтобы его продольные размеры уменьшились в 2 раза?
Ответ: а) v=2,6 м/с; б) v=26×км/с; в) v=2,6×108 м/с; г) v= =2,6×105 м/с; д) v=2,6×103 м/с.
2.1.103. При какой относительной скорости v движения релятивистское сокращение длины движущегося тела составляет 25%?
Ответ: а) v=1,58×108 м/с; б) v=1,68×108 м/с; в) v=1,78×108 м/с;
г) v=1,88×108 м/с; д) v=1,98×108 м/с.
2.1.104. Мезон, входящий состав космических лучей, движется со скоростью, составляющей 95% скорости света. Какой промежуток времени Dt по часам неподвижного наблюдателя соответствует одной секунде «собственного времени» мезона?
Ответ: а) Dt=32 с; б) Dt=3,2 с; в) Dt=0,32 с; г) Dt=4,2 с; д) Dt=42 с.
2.1.105. Во сколько раз увеличивается продолжительность существования нестабильной частицы по часам неподвижного наблюдателя, если она начинает двигаться со скоростью, составляющей 99% скорости света?
Ответ: а) 1,7; б) 7; в) 2,7; г) 0,7; д) 3,7.
2.1.106. Вычислить импульс протона в МэВ/с, что его кинетическая энергия T=500 МэВ.
Ответ: а) р=1,09×103 МэВ/с; б) р=1,19×103 МэВ/с; в) р= =1,29×103 МэВ/с; г) р=1,39×103 МэВ/с; д) р=1,49×103 МэВ/с.
2.1.107. Определить импульс р электрона, движущегося со скоростью v=0,9с, где с – скорость света в вакууме.
Ответ: а) р=6,6×10-22 кг×м/с; б) р=5,6×10-22 кг×м/с; в) р=
=4,6×10-22 кг×м/с; г) р=3,6×10-22 кг×м/с; д) р=2,6×10-22 кг×м/с.
2.1.108. Определить кинетическую энергию Т электрона, движущегося со скоростью v=0,9с, где с – скорость света в вакууме.
Ответ: а) Т=1,26×10-12 Дж; б) Т=1,16×10-12 Дж; в) Т=1,06×10-12 Дж; г) Т=0,96×10-12 Дж; д) Т=0,94×10-12 Дж.
2.1.109. До какой энергии Wк можно ускорить протоны в циклотроне, если относительное увеличение массы частицы не должно превышать 5%? (mp=1,67×10-27 кг; qp=1,6×10-19 Кл; c=3×108 м/с).
Ответ: а) Wк=37 МэВ; б) Wк=27 МэВ; в) Wк=17 МэВ; г) Wк= =47 МэВ; д) Wк=57 МэВ.
2.1.110. Какую ускоряющую разность потенциалов U должен пройти электрон, чтобы его скорость составила 95% скорости света?
Ответ: а) U=2,1 МВ; б) U=3,1 МВ; в) U=1,1 МВ; г) U=0,1 МВ; д) U=2,9 МВ.
2.1.111. Найти изменение энергии DW, соответствующее изменению массы Dm=mе (масса электрона me=9,1×10-31 кг; скорость света в вакууме с=3×108 м/с).
Ответ: а) DW=6,2×10-14 Дж; б) DW=10,2×10-14 Дж; в) DW= =2×10-14 Дж; г) DW=8,2×10-14 Дж; д) DW=8×10-14 Дж.
2.1.112. Какому изменению массы Dm соответствует изменение энергии на DW=4,19 Дж? Скорость света в вакууме с=3×108 м/с.
Ответ: а) Dm=4,6×10-17 кг; б) Dm=4,6×10-10 кг; в) Dm=5,6×10-17 кг; г) Dm=5,6×10-10 кг; д) Dm=6,6×10-17 кг.
2.1.113. Какую долю b скорости света должна составлять скорость частицы, чтобы ее кинетическая энергия была равна ее энергии покоя?
Ответ: а) b=56,6%; б) b=86,6%; в) b=66,6%; г) b=6,6%;
д) b=46,6%.
2.1.114. Синхрофазотрон дает пучок протонов с кинетической энергией Wк=10 ГэВ. Какую долю b скорости света составляет скорость протонов в пучке? (mp=1,67×10-27 кг; c=3×108 м/с).
Ответ: а) b=0,96; б) b=0,996; в) b=0,900; г) b=0,886;
д) b=0,796.
2.1.115. Частица движется со скоростью, равной половине скорости света. Во сколько раз масса движущейся частицы больше массы покоящейся?
Ответ: а) m/m0=1,115; б) m/m0=1,215; в) m/m0=1,315; г) m/m0= =1,415; д) m/m0=1,515.
2.1.116. С какой скоростью движется частица, если ее масса в три раза больше массы покоя?
Ответ: а) v=2,93×108 м/с; б) v=2,83×108 м/с; в) v=2,73×108 м/с;
г) v=2,63×108 м/с; д) v=2,53×108 м/с.
2.1.117. Во сколько раз масса протона больше массы электрона, если обе частицы имеют одинаковую кинетическую энергию Wk=1000 МэВ?
Ответ: а) n=1,74; б) n=1,84; в) n=1,94; г) n=2,04; д) n=2,06.
2.1.118. Кинетическая энергия электрона Wk=10 МэВ. Во сколько раз его масса больше массы покоя?
Ответ: а) n=19,6; б) n=20,6; в) n=21,6; г) n=22,6; д) n=23,6.
2.1.119. Кинетическая энергия протона Wk=10 МэВ. Во сколько раз его масса больше массы покоя?
Ответ: а) n=1,41; б) n=1,31; в) n=1,21; г) n=1,11; д) n=1,01.
2.1.120. Кинетическая энергия электрона Wk=0,8 МэВ. Определить импульс электрона.
Ответ: а) p=7,8×10-22 (кг×м)/с; б) p=7,4×10-22 (кг×м)/с; в) p= =6,8×10-22 (кг×м)/с; г) p=6,4×10-22 (кг×м)/с; д) p=5,4×10-22 (кг×м)/с.
