Кинематика и динамика. Волновые процессы. Акустика.
Примеры решения задач
1. Уравнение движения материальной точки вдоль оси X имеет вид X=2+t-0,5t2. Найти: координату X, скорость | v | и ускорение | a | точки в момент времени t=2 с.
Решение. Координату X найдем, подставив в уравнение движения числовые значения коэффициентов A, B, C и времени t:
X=(2+1×2 - 0,5 22)=2 м.
Мгновенная скорость относительно оси X есть первая производная от координаты по времени:
.
Ускорение точки найдем, взяв первую производную от скорости по времени:
.
В момент времени t=2 с
v=(1-3×0,5×2)= -5 м/с;
a=6×(–0,5)×2= -6 м/с2.
Ответ: X=2 м; v= -5 м/c; a= -6 м/с2.
2. Точка движется по кривой согласно уравнению x=6t-t3/8. Найти среднюю скорость движения точки в промежутке времени от t1=2,0 с до t2=6,0 c.
Решение. При движении материальной точки в некотором направлении, она может совершать движение как в одном, так и в другом направлении, поэтому перед решением такого типа задач необходимо провести исследование: 1). При каком значении времени t скорость точки равна нулю? 2). С каким по знаку ускорением движется точка?
1). Для определения момента времени t, при котором скорость движения равна нулю, находим
.
Решая полученное уравнение, имеем:
Следовательно, в момент времени t=4с скорость материальной точки равна нулю.
2). Установим знак ускорения, с которым движется точка:
.
Таким образом, в момент времени t=4с материальная точка, движущаяся в направлении возрастания x, изменит направление своего движения на противоположное.
По определению средняя скорость движения равна отношению пройденного пути к тому промежутку времени, в течение которого совершалось движение. В нашем случае
,
где 
– расстояние, пройденное точкой за время от t=0 до t1;
– расстояние, пройденное точкой за время от t1 до t2;
t – время движения точки.
.
Тогда
.
Подставляя численные значения, будем иметь
м/с.
Ответ: <v>=3 м/с.
3. Маховик движется равноускоренно. Найти угол, который составляет вектор полного ускорения любой точки маховика с радиусом в тот момент, когда маховик совершит первые 2 оборота.
Решение. Выберем любую точку «М» маховика и сделаем чертеж (рис. 1.1). Из чертежа можно установить, что
.
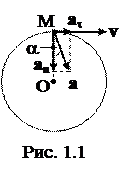
Из законов кинематики вращательного движения известно, что
w02-w2=2 ej.
Так как по условию задачи
w0 =0, j =2p×N, аt=er, a n= w2r, w2 =4pNe.
Тогда
. a=2°17¢.
Ответ: a=2°17¢.
4. По дуге окружности радиусом 10 м вращается точка. В некоторый момент времени нормальное ускорение точки равно 4,9 м/с2. Вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60o. Найти скорость и тангенциальное ускорение точки.
Решение. Известно, что нормальное ускорение характеризует изменение линейной скорости по направлению. Ее численное значение равно
,
откуда
.
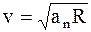Полное линейное ускорение
.
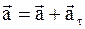Следовательно,
.
Из предварительно построенного чертежа можно установить (рис. 1.2), что
,
тогда
.
Подставляя численные значения, будем иметь
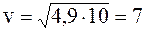м/с;
м/с2.
Ответ: v=7 м/с; аt=8,5 м/с2.
5. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебательных движениях, происходящих согласно уравнениям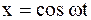 
и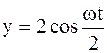 
. Найти уравнение траектории движения точки и построить траекторию с соблюдением масштаба.
Решение. Для отыскания уравнения траектории движения точки необходимо из уравнений движения исключить время. В рассматриваемом случае применяем формулу косинуса половинного угла
.
Для рассматриваемого случая
;
Имеем
.
Так как 
, то
.
Полученное уравнение и является уравнением траектории движения, которое представляет собой уравнение параболы, ось которой лежит на оси OX. Из уравнений движения точки амплитуда колебаний точки по оси OX равна 1, по оси OY – 2. Следовательно, абсциссы всех точек траектории заключены в пределах от
-1 до +1, а ординаты от 0 до +2.
Для построения траектории движения по его уравнению найдем значения y, соответствующие ряду значений x, удовлетворяющих условию x<1:
| x | -1,00 | -0,75 | -0,50 | -0,25 | 0,25 | 0,50 | 0,75 | 1,00 | |
| 0,71 | 1,00 | 1,22 | 1,41 | 1,58 | 1,73 | 1,87 | 2,00 |
По данным таблицы можно построить траекторию движения материальной точки (рис. 1.3).
6. Диск радиусом 0,1м вращается согласно уравнению j=10+20t-2t2. Определить по величине и направлению полное ускорение точек на окружности диска для момента времени t=4с.
Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения a t, направленного по касательной к траектории, и нормального ускорения a n, направленного к центру кривизны траектории:
.
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
; 
,
где w – угловая скорость тела;
e – его угловое ускорение;
r – расстояние точки от оси вращения.
Подставляя выражения at и an в формулу полного ускорения, будем иметь
.
Угловая скорость вращающегося тела равна первой производной от угла поворота по времени. В нашем случае
.
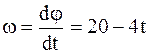В момент времени t=4с угловая скорость точек на окружности диска
рад/с.
Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени
рад/с2.
Это выражение углового ускорения не содержит времени. Следовательно, угловое ускорение имеет постоянное значение, не зависящее от времени.
Подставляя найденные значения w и e, заданное значение r в формулу полного ускорения, имеем
м/с.
По вышеприведенным формулам 
; , найдем значения at и an:
аt= -4×0,1= -0,4 м/с2; аn =4×4×0,1=1,6 м/с2.
Направление полного ускорения определится, если найти углы, которые вектор полного ускорения образует с касательной к траектории или с нормалью к ней:
; 
.
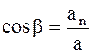Подставляя эти значения и значение полного ускорения для косинусов углов, будем иметь
cosa=0,4/1,65 =0,242; cosb=1,6/1,65=0,97, что соответствует углам a=76°, b=14°.
Ответ: a=1,65 м/с2; a=76 °, b=14°.
7. Две материальные точки движутся согласно уравнениям x1=10+t – 2t2 и x2=3+2t+0,2t2. В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в момент времени t=3с?
Решение. Известно, что линейная скорость численно равна первой производной от перемещения по времени. В нашем случае, так как
x1 = 10+t – 2t2 и x2=3 +2t +0,2t2,
то
; 
.
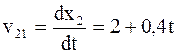По условию задачи v1=v2, следовательно,
1 – 4t=2 +0,4
откуда
-4,4t=1, t= -0,23 с.
Знак «минус«означает, что скорости точек были равны до начала отсчета времени.
Линейное ускорение численно равно первой производной от скорости по времени. В нашем случае
м/с2; 
м/с2.
Ответ: t= -0,23с; a1= -4 м/с2; a2=0,4 м/с2.
8. Точка совершает гармонические колебания с частотой 10Гц. В момент, принятый за начальный, точка имела максимальное смещение: xmax=1 мм. Написать уравнение колебаний точки.
Решение. В общем виде уравнение гармонических колебаний точки можно записать в виде
x=A×sin(w0t+j01)
или
x=A cos(2pn0t+j02),
где А – амплитуда колебаний;
w0 – циклическая частота;
t – время;
j01, j02 – начальные фазы.
По определению, амплитуда колебаний A= xmax. Циклическая частота w связана с частотой n0 соотношением w0=2pn0.
Начальная фаза колебаний зависит от формы записи. В момент времени t=0 уравнения гармонических колебаний примут вид
xmax=A×sin j01
или
xmax=A×cosj02,
откуда начальные фазы колебаний
;
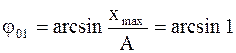или
;
,
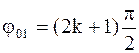где k=0,1,2,.....
Изменение фазы на 2p не изменит состояние колебательного движения, поэтому можно принять k=0, тогда j01=p/2, а j02 =0.
С учетом полученных результатов, уравнения колебаний примут вид
или
.
9. К концам однородного стержня приложены две противоположно направленные силы: F1=40Н и F2=100Н. Определить силу Т, приложенную к поперечному сечению, которое делит стержень на две части в отношении 1:2 (рис. 1.4).
Решение. Если бы силы F1 и F2 были равны между собой, то сила T, растягивающая стержень в любом сечении, была бы одинаковой и равной силам, приложенным к концам стержня. Стержень в этом случае находился бы в покое.
Но так как сумма сил, действующих на стержень, отлична от нуля, то стержень будет двигаться с ускорением, величина и направление которого определяются по второму закону Ньютона:
,
где m – масса стержня.
Так как обе силы действуют вдоль прямой, то геометрическую сумму можно заменить алгебраической:
.
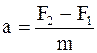При ускоренном движении стержня силы, растягивающие его, в разных сечениях различны. Для определения этих сил применим следующий прием: разделим стержень на две части в интересующем нас сечении и отбросим одну из них, на пример левую. Действие левой части на правую заменим силой T. В результате действия разности сил F2 – T оставшаяся правая часть стержня массой m должна двигаться с ускорением, равным по величине и направлению прежнему ускорению
.
Так как стержень однородный, то m1=m/3 и, следовательно,
.
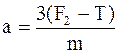Приравнивая
.
Выражая из полученного равенства силу, растягивающую стержень T, находим
.
Подставив значения F2 и F1, получим
T=100 – (100 – 40)/3=80 (Н).
Ответ: T=80 Н.
10. В лифте на пружинных весах находится тело массой 10 кг. Лифт движется с ускорением 2 м/с2. Определить показания весов в двух случаях, когда ускорение лифта направлено: 1) вертикально вверх; 2) вертикально вниз (рис. 1.5).
Решение. Определить показания весов – это значит найти вес тела G, т.е. силу, с которой тело действует на пружину. Но эта сила, по третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости N (силе реакции опоры), с которой пружина действует на тело, т.е.
ê G ê=ê N ê.
Следовательно, задача определения показания весов сводится к нахождению реакции опоры. Задачу можно решать как в инерциальной, так и неинерциальной системе отсчета.
1). Решение в инерциальной системе отсчет. На тело действуют две силы: сила тяжести P и сила N. Направим ось z вертикально вверх. Запишем уравнение движения в векторной форме
.
Спроецируем данное уравнение на ось z. Индекс «z«у проекций опустим, так как проекции и сами векторы совпадают по величине. Направление проекций учтем знаком плюс или минус:
,
откуда
,
т.е.
.
При вычислении показания весов следует учесть знак ускорения:
a) ускорение направлено вертикально вверх (а>0), тогда
G=10(9,81+2)=118Н;
б) ускорение направлено вертикально вниз (а<0), тогда
G=10(9,81 - 2)=78Н.
Отметим, что ни модуль, ни направление скорости лифта не влияют на показания весов. Существенны лишь величина и направление ускорения.
2). Решение в неинерциальной системе отсчет, т.е. в системе, движущейся ускоренно вместе с лифтом.
В этой системе отсчета законы Ньютона не выполняются. Однако если к телу, в соответствии с принципом Даламбера дополнительно к действующим на него силам приложить силу инерции
F i= -m a,
где a – ускорение системы отсчета, то с учетом этой силы законы Ньютона будут справедливы.
В этом случае на тело будут действовать три силы: сила тяжести P, сила упругости N и сила инерции F i. Под действием этих сил тело в данной неинерциальной системе отсчет покоится. Это значит, что вместо уравнений динамики (законов Ньютона) можно воспользоваться законами статики. Если тело под действием системы сил покоится, геометрическая сумма этих сил равна нулю. В данном случае это приводит к равенству
P + N + F =0.
Спроецируем все силы на ось z. С учетом знака проекций будем иметь
N – P – ma=0,
откуда
N=G=m(g+a),
что совпадает с результатом, полученным при решении задачи в инерциальной системе отсчета.
Ответ: 1) G=118Н; 2) G=78Н.
11. При падении тел с большой высоты его скорость vуст при установившемся движении достигает 80 м/с. Определить время t, в течение которого, начиная от момента начала падения, скорость становится равной 0,5vуст. Силу сопротивления воздуха принять пропорциональной скорости тела (рис. 1.6).
Решение. На падающее тело действуют две силы: сила тяжести m g и сила сопротивления воздуха F с. Сила сопротивления воздуха при установившемся движении по условию задачи пропорциональна скорости тела и противоположна ей по направлению:
,
где k – коэффициент пропорциональности, зависящий от размеров, формы тела и от свойств окружающей среды.
Запишем уравнение движения тела в соответствии со вторым законом Ньютона в векторной форме:
; 
.
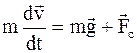Спроецируем все векторные величины на вертикально направленную ось и запишем уравнение движения для проекций:
.
После разделения переменных получим
.
Проинтегрируем полученное уравнение, учитывая, что при изменении времени от нуля до t (искомое время) скорость возрастает от нуля до 0,5vуст:
;
.
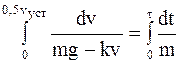Подставим пределы интегрирования в левую часть равенства:
.
Из полученного соотношения найдем искомое время:
Входящий в выражение коэффициент пропорциональности k определим из следующих соображений. При установившемся движении (скорость постоянна) алгебраическая сумма проекций сил (на выбранную ось), действующих на тело, равна нулю, т.е.
,
откуда
.
Подставив найденное значение k, окончательно для времени t, будем иметь:
.
Проверка размерности в данном случае не обязательна, так как результат очевиден. Подставив в формулу численные значения и произведя вычисления, получим
c.
Ответ: t=5,66с.
12. Деревянный брусок массой 350 г, находящийся на горизонтальной плоскости, привязан к нити, которая перекинута через блок. Другим концом нить прикреплена к грузу массой 265 г. Коэффициент трения между бруском и плоскостью 0,45. Пренебрегая массой блока и трением при его вращении, сопротивлением воздуха, считая нить невесомой и нерастяжимой, определить ускорение системы и натяжение нити (рис. 1.7).
Решение. Для решения задачи воспользуемся основными уравнениями динамики поступательного движения. Для этого рассмотрим силы, действующие на каждый груз в отдельности. На первый груз действуют: сила тяжести m g, реакция опоры N, сила натяжения нити T 1 и сила трения F. На второй – сила тяжести m g и сила натяжения нити T 2.
На основании второго закона Ньютона запишем уравнения движения каждого из грузов в векторной форме:
;
.
Так как нить невесома и нерастяжима, то a 1= a 2= a, T 1= T 2= T. С учетом данного замечания уравнения движения грузов будут иметь вид
;
.
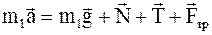Произвольно выбираем направление движения системы (например: левый груз движется слева направо, второй – вниз) и проектируем уравнения движения на выбранное направление. С учетом знаков проекций соответствующих векторов и | F тр|=mm1g, уравнения движения перепишем в виде
;
.
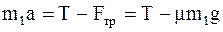Имеем систему двух уравнений с двумя неизвестными, решая которую находим
;
.
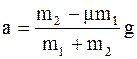Проверив размерность и подставив численные значения входящих в полученные формулы величин, получаем
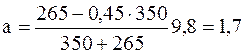м/с2;
Н.
Ответ: a=1,7 м/с2, T=2,1 Н.
13. Тело массой m подвешено к концу нерастяжимой нити длиной l. Точка крепления нити к опоре движется относительно Земли с постоянным ускорением a, образующим угол a с горизонтом. Найти угол отклонения нити от вертикали j и силу, с которой тело действует на нить (рис. 1.8).
Решение. Для решения задачи воспользуемся основными уравнениями динамики поступательного движения. На движущееся тело действуют сила тяжести m g и сила натяжения нити T. Запишем уравнение движения в векторной форме:
.
Выбираем систему отсчет XOY, в центр пересечения осей которой помещаем точку крепления нити к опоре. Спроектируем уравнение движения на оси координат
OX: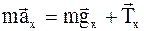 
;
OY: 
,
где ax=a×cosa, mgx=0, Tx=T sina, ay=a×sina, mgy= – mg, Ty=T cosj.
Тогда уравнения движения по направлениям X и Y будут иметь вид
;
.
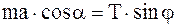Решая полученную систему двух уравнений с двумя неизвестными, будем иметь
;
.
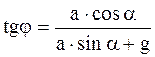Проанализируем полученный результат:
1) при tgj=0 – тело движется вверх или вниз
,
где «плюс» соответствует движению тела вверх; «минус» – вниз.
2) если g=a, то при движении вниз T=0 – «свободное падение».
14. Через блок в виде сплошного диска, имеющего массу 80 г, перекинута невесомая, нерастяжимая, гибкая нить, к концам которой подвешены грузы массами 100 г и 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Сопротивлением воздуха и массой нити пренебречь (рис. 1.9).
Решение. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый и второй грузы действуют силы тяжести и натяжения нити: m1 g, T 1, m2 g, T 2; на блок – моменты сил | M 1|=T1'r и | M 2|=T2'r (при этом M =I e), где соответственно:
T 1 и T 2 – силы натяжения нити, действующие на грузы;
T1' и T2' – силы натяжения нити, действующие на блок;
I – момент инерции блока;
e – угловое ускорение.
Составим уравнения движения каждого из тел системы «грузы – блок«в векторной форме:
;
;
.
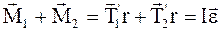Спроецируем первые два уравнения на ось x, которую направим вертикально вниз. С учетом знаков проекций будем иметь
;
;
.
C учетом того, что нить невесома и нерастяжима ê a 1ê=ê a 2ê=a,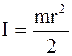 
, сила ê T 1ê=ê T 1'ê, | T 2ê=ê T 2'ê (согласно третьему закону Ньютона) написанные выше уравнения перепишем в виде
;
;
.
Решая систему трех уравнений с тремя неизвестными, найдем интересующее нас ускорение
.
Отношение масс в правой части полученной формулы есть величина безразмерная. Поэтому числовые значения масс можно выразить в граммах, как они даны в условии задачи. Числовое значение ускорения g надо взять в единицах системы СИ. После подстановки получим
a= 
м/с2.
Ответ:а=2,88 м/с2.
15. Диск радиусом 20 см и массой 7 кг вращается согласно уравнению j=3 – t+0,1t3. Определить закон, по которому изменяется вращающий момент, действующий на диск. Определить момент сил в момент времени t=2с (рис. 1.10).
Решение. Для нахождения закона, по которому меняется вращающий момент, действующий на диск, воспользуемся основным уравнением динамики вращательного движения:
M =I e,
где I – момент инерции диска относительно выбранной оси вращения;
e – угловое ускорение.
Момент инерции диска относительно оси, проходящей через его геометрический центр, определяется по формуле:
,
где m – масса диска;
R – радиус диска.
Известно, что угловое ускорение – это первая производная от угловой скорости по времени или вторая производная от угла поворота по времени.
В нашем случае
.
Тогда закон, по которому изменяется вращающий момент, действующий на диск, будет иметь вид
.
Для определения численного значения момента сил, действующего на диск в момент времени t=2с, необходимо в полученную формулу подставить численные значения величин, указанных в условии задачи.
После проверки размерностей полученного результата и вычислений будем иметь
M=0,3×7×0,04×2=0,168 Нм.
Ответ: М=0,168 Нм.
16. Тонкий стержень длиной 4 см и массой 0,6 кг вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение движения стержня j=t+0,1t3. Определить вращающий момент в момент времени t=2с (рис. 1.11).
Решение. Для нахождения вращающего момент, действующего на стержень, воспользуемся основным уравнением динамики вращательного движения:
M =I e,
где I – момент инерции стержня относительно выбранной оси вращения;
e – угловое ускорение.
Момент инерции стержня относительно выбранной оси, проходящей через его геометрический центр, определяется по формуле:
,
где m – масса стержня;
l – его длина.
Известно, что угловое ускорение – это первая производная от угловой скорости по времени или вторая производная от угла поворота по времени.
В нашем случае
.
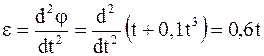Тогда вращающий момент, действующий на стержень, будет равен
.
Для определения численного значения момента сил, действующего на стержень в момент времени t=2с, необходимо в полученную формулу подставить численные значения величин, указанных в условии задачи.
После проверки размерностей полученного результата и вычислений окончательно имеем
M=0,05×0,6×0,16×2=0,01 Нм.
Ответ: М=0,01 Нм.
17. Диск радиусом 20 см и массой 50 кг вращается с частотой 8 об/с. При торможении он остановился через 40с. Определить тормозящий момент (рис. 1.12).
Решение. Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде
.
где d L z – изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика за время dt;
M z – момент внешних сил (в нашем случае момент сил трения – тормозящий момент), действующих на маховик относительно той же оси.
Момент сил трения можно считать не изменяющимся с течением времени, поэтому интегрирование выше написанного уравнения приводит к выражению
.
При вращении твердого тела относительно неподвижной оси изменение момента импульса
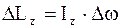
где Iz – момент инерции маховика относительно оси z;
Dw – изменение угловой скорости маховика.
Приравняв правые части выше написанных равенств, получим
,
откуда
.
Момент инерции маховика в виде сплошного диска определяется по формуле
.
Изменение угловой скорости Dw=w2 – w1 – выразим через конечную n2 и начальную n1 частоты вращения, пользуясь соотношением w=2pn:
Dw=2p(n2 – n1).
Подставив значения Iz и Dw в формулу Mz, получим
.
Проверим, совпадают ли размерности правой и левой частей в полученном соотношении.
Размерность левой части:
dimM=dim(FR)=dimF×dimR=LMT – 2L=L2MT – 2.
Размерность правой части:
,
что совпадает с размерностью левой части.
Подставив численные значения и произведя вычисления в системе СИ, будем иметь
Нм.
Знак «минус» показывает, что силы трения оказывают на маховик тормозящее действие.
Ответ: M= -1Нм
18. Через блок радиусом 4 см перекинули шнур, к концам которого привязаны грузы массами 50 г и 60 г. При этом блок пришел в движение с ускорением 1,5 с-2. Определить момент инерции блока. Трение при вращении не учитывать (рис. 1.13).
Решение. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на блок и на каждый груз в отдельности. На первый и второй грузы действуют силы тяжести и натяжения нити: m1 g, T 1, m2 g, T 2. На блок моменты сил M 1= T 1'r и M 2= T 2'r (при этом M =I e), где соответственно:
T 1 и T 2 – силы натяжения нити, действующие на грузы;
T 1' и T 2' – силы натяжения нити, действующие на блок;
I – момент инерции блока;
e – угловое ускорение.
Составим уравнения движения каждого из телу системы «грузы – блок» в векторной форме:
;
;
.
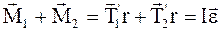Спроецируем эти уравнения на ось x, которую направим вертикально вниз. С учетом знаков проекций будем иметь:
;
;
.
С учетом того, что нить невесома и нерастяжима ç a 1ç=ç a 2ç=a, a=R e, силы ç T 1ç=ç T 1'ç,ç T 2ç=ç T 2'ç (согласно третьему закону Ньютона) написанные выше уравнения перепишем в виде:
;
;
.
Решая систему трех уравнений с тремя неизвестными, найдем интересующий нас момент инерции
.
После проверки размерностей левой и правой частей, полученного соотношения и подстановки численных значений, входящих в него величин, будем иметь
кгм2.
Ответ: I=2,52×10-3 кгм2.
19. Стержень длиной 4 см колеблется около оси, перпендикулярной стержню и проходящей через один из его концов. Определить период колебаний такого маятника (рис. 1.14).
Решение. Такой стержень можно рассматривать как некоторый 
физический маятник.
Физический маятник – твердое тело, способное совершать колебательное движение относительно оси, на которой оно подвешено. При этом ось колебаний не проходит через центр тяжести.
Уравнение движения физического маятника, при малых углах отклонения, имеет вид:
.
где m – масса физического маятника;
I – его момент инерции относительно оси колебаний;
d – кратчайшее расстояние между осями, одна из которых параллельна данной и проходит через центр тяжести;
j – угол отклонения маятника от положения равновесия.
Решением этого уравнения является выражение вида
j=jo sin(wt +a).
Решая дифференциальное уравнение второго порядка, для периода колебаний физического маятника можно получить
,
где 
– приведенная длина физического маятника.
В рассматриваемом случае момент инерции физического маятника определяем по теореме Штейнера:
I=I0+mr2,
где I0=ml2/12 – момент инерции стержня относительно оси, проходящей через центр тяжести;
r=l/2= – расстояние от одного из концов стержня до центра тяжести.
Подставив значения I и r для момента инерции стержня, будем иметь:
.
По условию задачи d=l/2. Тогда период колебаний стержня
.
Размерность полученного результата очевидна. Подставляя численные значения величин, входящих в формулу, и произведя вычисления, определяем период колебаний стержня:
с.
Ответ: T=0,9с.
20. Материальная точка массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид x=0,2×sin8pt. Найти возвращающую силу в момент времени t=0,1с.
Решение. Так как материальная точка совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением:
Fв=-kx,
где k – коэффициент квазиупругой силы;
x=0,2×sin8pt – смещение колеблющейся точки.
Коэффициент k выразим через круговую или циклическую частоту:
k=mw2.
Подставив значения x и k в формулу возвращающей силы, будем иметь
Fв=mw2x=mw2A×sinwt.
Проверив размерности левой и правой частей уравнения, подставив численные значения, произведем вычисления:
F=0,01×64×3,142×0,2×sin(0,8×3,14)= 0,75Н.
Ответ: F=0,75Н.
21. Диск радиусом 10 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период и частоту колебаний такого физического маятника (рис. 1.15).
Решение. Такой диск можно рассматривать как некоторый физический маятник. Физический маятник – твердое тело, способное совершать колебательное движение относительно оси, на которой оно подвешено, при этом ось колебаний не проходит через центр тяжести.
Уравнение движения физического маятника имеет вид:
.
где m – масса физического маятника;
I – его момент инерции относительно оси колебаний;
d – кратчайшее расстояние между осями, одна из которых параллельна данной и проходит через центр тяжести;
j – угол отклонения маятника от положения равновесия.
Решением этого уравнения является выражение вида
j=jo sin(wt +a).
Решая дифференциальное уравнение второго порядка, для периода колебаний физического маятника можно получить
,
где – приведенная длина физического маятника.
В рассматриваемом случае момент инерции физического маятника определяем по теореме Штейнера:
I=I0+mr2,
где I=mR2/2 – момент инерции диска относительно оси, проходящей через центр тяжести;
r=R/2 – расстояние между осями.
Подставив значения I и для момента инерции диска, будем иметь:
.
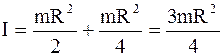Тогда период колебаний диска
,
а частота
.
Размерность полученного результата очевидна. Подставляя численные значения величин, входящих в формулу, и произведя вычисления, находим период и частоту колебаний диска:
с;
Гц.
Ответ: T=1,07с, n=0,94Гц.
22. Два маховика, выполненные в виде дисков радиусом 0,4 м и имеющие массу 100 кг каждый, вращающиеся с частотой 480об/мин, были предоставлены самим себе. Под действием трения валов о подшипники первый маховик остановился через 1 мин 20с; второй маховик до полной остановки сделал 240 оборотов. Определить моменты сил трения вала о подшипники у каждого маховика и сравнить их между собой.
Решение. 1. Найдем момент сил трения, действующий на первый маховик. Для этого воспользуемся основным уравнением динамики вращательного движения в виде
М1×Dt=Iw2 – Iw1,
где M1 – вращающий момент (в данном случае искомый момент силы трения);
Dt – время действия вращающего момента;
I – момент инерции маховика;
w1 – начальная угловая скорость вращения маховика;
w2 – его конечная угловая скорость.
Решая это уравнение относительно M, получим:
.
С учетом того, что I=mR2/2, w1=2pn1, w2 =0 окончательно имеем:
.
Подставим в полученное выражение числовые значения входящих в него величин и произведем вычисления:
Нм.
Знак «минус» показывает, что силы трения оказывают на маховик тормозящее действие.
2. Найдем момент сил трения, действующих на второй маховик. Для этого воспользуемся основным уравнением динамики вращательного движения в виде
M2=Ie,
где M2 – момент сил трения;
I – момент инерции второго маховика относительно оси, проходящей через его геометрический центр;
e – угловое ускорение.
Момент инерции диска можно определить по формуле
.
Для определения углового ускорения воспользуемся кинематическими уравнениями, характерными для замедленного движения:
;
,
где w0 – угловая скорость маховика до начала действия сил торможения;
w=0 – конечная угловая скорость маховика (он остановился);
j – угловое расстояние, пройденное маховиком до полной остановки.
Решая систему двух уравнений с двумя неизвестными (e и t) для углового ускорения e, получим
.
Подставляя I и e в ранее полученную формулу для момента сил торможения, окончательно будем иметь
,
где j=2pN, 
.
Подставим в полученное для M2 выражение числовые значения входящих величин, произведем вычисления:
Нм.
Чтобы сравнить полученные значения моментов сил трения, найдем отношение их абсолютных значений
.
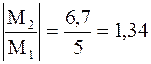Таким образом, момент сил трения, действующий на второй маховик, в 1,34 раза больше, чем на первый.
Ответ: M1= -5 Нм, M2= -6,64 Нм, M2/M1=1,34.
23. В незатухающей бегущей волне задана точка M, отстоящая от источника колебаний на расстоянии y=l/12 в направлении распространения волны. Амплитуда колебаний А=0,050 м. Считая в начальный момент времени смещение точки P, находящейся в источнике, максимальным, определить смещение от положения равновесия точки M для момента времени t=T/6, а также разность фаз колебаний точек M и P.
Решение. Смещение точки М можно найти с помощью уравнения бегущей волны
,
где x – смещение точки от положения равновесия, находящейся на расстоянии y от источника гармонических колебаний;
А – амплитуда колебаний;
w – циклическая частота;
j0 – начальная фаза колебаний.
Используя условие задачи, преобразуем это уравнение так, чтобы в него вошли длина волны l, и период T колебаний. Учитывая соотношение между периодом колебаний и циклической частотой и равенство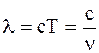 
, где T – период колебаний, 
– частота колебаний, получим
. (1)
Чтобы найти начальную фазу j0, воспользуемся начальными условиями задачи: если t=0, y=0, то x=А. При этих значениях t, y, x из уравнения (1) имеем
.
Откуда
.
Подставив числовые значения величин, А, t/T, y/l, j0 в уравнение (1), получим первый ответ:
м.
Для вычисления разности фаз (jМ – jР) колебаний точек М, Р учтем, что для точки Р координата y=0. Следовательно, в любой момент t фаза точки Р, т.е. аргумент синуса в уравнении (1), равна
.
Тогда
. (2)
Подставив в формулу (2) числовые значения, найдем
.
Знак «минус» в полученном результате указывает на то, что колебания точки М отстают по фазе от колебаний источника на угол 
.
.
Ответ: x=0,044 м; φМ-φР=-π/6.
24. Плоская волна распространяется вдоль прямой со скоростью v=20 м/с. Две точки, находящиеся на этой прямой на расстояниях x1=12 м и x2=15 м от источника волн, колеблются с разностью фаз Dj=0,75p. Найти длину волны l, написать уравнение волны и найти смещение указанных точек в момент t=1,2 с, если амплитуда колебаний А=0,1 м.
Решение. Точки, находящиеся друг от друга на расстоянии, равном длине волны, l колеблются с разностью фаз, равной 2p; точки находящиеся на любом расстоянии Dx, колеблются с разностью фаз, равной
.
Решая это равенство относительно l, получаем
. (1)
Подставив числовые значения величин, входящих в выражение (1), и выполнив арифметические действия, получим
м.
Для того чтобы написать уравнение плоской волны, необходимо найти циклическую частоту w. Так как w=2p/T 
, то
с –1.
Зная амплитуду колебаний А, циклическую частоту w и скорость v распространения волны, можно написать уравнение плоской волны для данного случая:
, (2)
где А=0,1 м; w=5p с – 1, v=20 м/с.
Чтобы найти смещение указанных точек, достаточно в уравнение (2) подставить значения t и x:
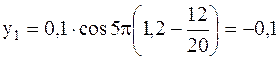м;
м.
Ответ: 
м; y1=-0,1 м; y2=-0,071 м.
25. Для определения частоты звуковых колебаний был применен интерференционный прибор, изображенный на рис. 44, где T – источник звука; А, В – два колена, представляющие собой полые металлические трубки (колено В – выдвижное); М – слуховая трубка. В зависимости от положения колена В наблюдатель регистрирует с помощью слуховой трубки усиление или ослабление звука. Для того, чтобы перейти от одного минимума звука к следующему, перемещают выдвижное колено на расстояние l=5,5 см. Считая скорость звука в воздухе при температуре опыта равной с=340 м/с, найти частоту звуковых колебаний.
Решение. В точке С (рис. 1.16) происходит интерференция звуковых волн, приходящих сюда от источника Т различными путями: ТАС и ТВС. Результат интерференции волн выражается условиями:
а) максимума
,
б) минимума
,
где n=0, 1, 2, 3¼.
Переместив колено В на расстояние l, изменяют тем самым разность хода волн 
на величину 2l:
, (1)
где D1, D2 – разность хода волн в начальном и конечном положениях колена.
Так как в обоих положениях громкость звука и связанная с ней амплитуда звуковых колебаний минимальны, то каждая из величин D1, D2 определяется соотношениями:
; 
. (2)
При этом, поскольку перемещение колена В соответствует двум соседним минимумам звука, должно выполняться соотношение
. (3)
Учитывая формулу (3), вычтем почленно уравнения (2) друг из друга. Тогда получим
. (4)
Сравнивая выражения (1) и (4), имеем
.
Частоту звуковых колебаний найдем, воспользовавшись соотношением
. (5)
Подставив в формулу (5) числовые значения величин, получим
Гц=3,1 кГц.
Ответ: ν=3,1·103 Гц=3,1 кГц.
26. Медный стержень длиной l=0,5 м закреплен в середине. Найти частоты возможных собственных продольных колебаний стержня.
Решение. Если какой – либо частице тела сообщить начальный импульс (например, ударить молотком по торцу стержня), то все частицы тела придут в колебательное движение – в теле установятся собственные колебания. Процесс распространения колебаний в закрепленном стержне представляет собой стоячие волны. Эти волны являются результатом интерференции двух встречных систем бегущих волн: падающих на границу данного тела с окружающей средой и отраженных от этой границы.
Частота собственных колебаний в стержне связана с длиной l бегущей волны соотношением
.
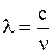При этом скорость с продольных волн в медном стержне можно найти по формуле
,
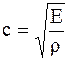где E – модуль упругости;
r – плотность материала стержня.
Тогда получим
.
Величины E, r для меди табличные, и задача сводится к определению длин волн, соответствующих собственным колебаниям стержня. Этим колебаниям всегда отвечает такое распределение по длине тела стоячих волн, которое удовлетворяет граничным условиям. На закрепленном конце тела должен быть узел смещений, на свободном конце– пучность. Следовательно, на концах данного стержня должны быть пучности смещений, а посередине его – узел смещений, так как в этом месте стержень закреплен. Один из возможных вариантов распределения стоячих волн по длине стержня изображен на рисунке 1.17. Здесь по оси x отложены расстояния точек стержня от его левого конца, по оси y – смещения точек стержня от положения равновесия, они имеют в некоторый момент времени, участвуя в продольных колебаниях (для поперечных колебаний приведенный график можно рассматривать как «моментальную» фотографию колеблющегося стержня). Пунктиром изображен график смещения спустя промежуток времени, равный Т/2. Точки А, В, С, D, E – узлы стоячей волны.
Из графика видно, что на всей длине стержня (от А до Е) должно укладываться четное число полуволн и еще две четверти волны. Таким образом, имеем
,
где n =0,1,2,3,…..
Отсюда
.
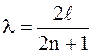Подставив это значение l в формулу для частоты, получим ответ:
.
Взяв из таблиц значения E=12×1010 Н/м2; r=8,9×103 кг/м3 и произведя вычисления найдем
n=3,7×103×(2n+1) Гц.
Значение n=0 соответствует частоте собственных колебаний n=3,7×103 Гц; значение n=1,2,3… соответствуют высшим гармоническим частотам.
Ответ: n=3,7×103×(2n+1) Гц.
27. Источник звука частотой 18 кГц приближается к неподвижно установленному резонатору, настроенному на акустическую волну l=1,75 см. Какой скоростью должен обладать источник звука, чтобы возбуждаемые им звуковые волны вызвали колебания резонатора? Температура воздуха 17 0С.
Решение. Согласно принципу Доплера, частота звука, воспринимаемая наблюдателем, зависит от скорости движения источника звука и скорости движения наблюдателя
, (1)
где n – частота звуковых волн, излучаемых источником;
с – скорость звука в данной среде;
u – скорость движения источника звука;
v – скорость движения наблюдателя;
n' – частота волн, воспринимаемых наблюдателем.
Учитывая, что наблюдатель остается неподвижным, т.е. что v=0, из формулы (1) получим
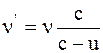. (2)
Отсюда
. (3)
В выражении (3) неизвестны числовые значения скорости звука c и частоты n'.
Скорость звука в газах зависит от природы газа и от температуры и определяется по формуле
, (4)
где 
– отношение молярных теплоемкостей газа;
R – универсальная газовая постоянная;
T – абсолютная температура газа;
m – молярная масса газа.
Чтобы волны, приходящие к резонатору, вызвали его колебания, частота воспринимаемых резонатором волн n' должна совпадать с собственной частотой резонатора nрез, т.е.
, (5)
где lрез – длина
