Степенные ряды и ряды Тейлора.
60.1. Найти предельную функцию для последовательности 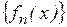 и построить ее график:
и построить ее график:
а)  ; б)
; б) 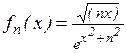 ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
60.2. Исследовать равномерную сходимость последовательности 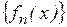 на заданном множестве Е:
на заданном множестве Е:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
60.3. Найти область сходимости и область абсолютной сходимости функциональных рядов:
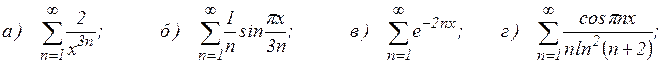

60.4. Доказать равномерную сходимость функционального ряда в указанном промежутке:

60.5. Найти область сходимости степенного ряда:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 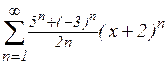 ;
;
д) 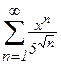 ; е)
; е)  ; ж)
; ж) 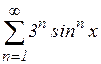 ; з)
; з)  .
.
60.6. Разложить функцию  в степенной ряд Тейлора с центром в точке
в степенной ряд Тейлора с центром в точке  и найти радиус сходимости R полученного ряда:
и найти радиус сходимости R полученного ряда:
а)  ; б)
; б) 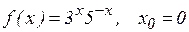 ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з) 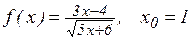 ;
;
и)  ; к)
; к) 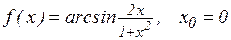 .
.
Обыкновенные дифференциальные уравнения.
Занятие № 61.
Уравнения с разделяющимися переменными.
61.1. Решить уравнения:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ;
;
ж)  ; з)
; з) 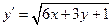 .
.
61.2. Найти решения, удовлетворяющие начальным условиям:
а) 
 ; б)
; б) 
 ;
;
в) 
 ; г)
; г) 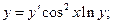
 .
.
Занятие № 62.
Однородные уравнения.
62.1. Решить уравнения:
а) 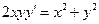 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
62.2. Найти решения, удовлетворяющие начальным условиям:
а)  ; б)
; б)  .
.
Занятие № 63.
Линейные уравнения первого порядка.
63.1. Решить уравнения:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
63.2. Найти решения, удовлетворяющие начальным условиям:
а) 
 ; б)
; б) 
 ; в)
; в) 
 .
.
63.3. Решить уравнения Бернулли:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Занятие № 64.
Уравнения в полных дифференциалах и
Не разрешенные относительно производной.
64.1. Решить уравнения в полных дифференциалах:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
64.2. Решить уравнения, не разрешенные относительно производной:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
Занятие № 65.
Линейные дифференциальные уравнения
С постоянными коэффициентами.
65.1. Решить однородные уравнения:
а) 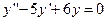 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
65.2. Решить неоднородные уравнения с правой частью специального вида:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 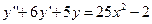 ;
;
ж)  ; з)
; з)  .
.
65.3. Решить уравнения методом вариации постоянных:
а)  ; б)
; б)  ; в)
; в)  .
.
Занятие № 66.
Системы дифференциальных уравнений.
66.1. Решить системы уравнений:
а) 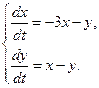 б)
б) 
в) 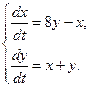 г)
г) 
д)  е)
е) 
ж)  з)
з) 
и)  к)
к) 
Рекомендуемая литература
1. И.В. Асташова, В.А. Никишкин. Геометрия и топология. М., МЭСИ, 2004.
2. А.Н. Малахов, В.А. Никишкин. Практикум по высшей математике. М., МЭСИ, 2004.
3. А.Н. Малахов, Н.И. Максюков, В.А. Никишкин. Высшая математика. М., МЭСИ, 2001.
4. Д.Б. Клетеник. Сборник задач по аналитической геометрии. М., Наука, 1975.
5. Л.А. Беклемишева, Ю.А. Петрович, И.А. Чубаров. Сборник задач по аналитической геометрии и линейной алгебре. М., Наука, 1987.
6. Н.Ш. Кремер. Высшая математика для экономистов. М.,ЮНИТИ, 1998.
7. Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу, М., ФИЗМАТЛИТ, 2007.
8. В.А. Малугин. Линейная алгебра. Задачи и упражнения. М.,ЭКСМО, 2006.
9. И.В. Проскуряков. Сборник задач по линейной алгебре.М., «Наука», 1978.
10. Д.К. Фаддеев, И.С. Соминский. Сборник задач по высшей алгебре. М., Наука», 1977.






