а) 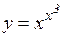 ; б)
; б)  ; в)
; в) 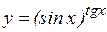 ; г)
; г)  .
.
27.4. Составить уравнения касательной и нормали к графику функции  в точке с абсциссой
в точке с абсциссой  .
.
27.5. Составить уравнение касательной к графику функции  , перпендикулярной прямой
, перпендикулярной прямой  .
.
27.6. Составить уравнение касательной к графику функции  , проходящей через точку
, проходящей через точку  .
.
27.7. Найти угол между параболами  и
и  в точке их пересечения.
в точке их пересечения.
27.8. Составить уравнение касательной к графику функции  , параллельной прямой, проходящей через точки (1;7) и (-2;-2).
, параллельной прямой, проходящей через точки (1;7) и (-2;-2).
27.9. Найти производные гиперболических функций  ,
,  ,
,  и
и  .
.
Найти производные неявных функций
а) 
б) 
в) 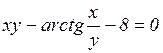
г) 
27.11. Найти производные функций 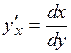 , заданных параметрически
, заданных параметрически
а) 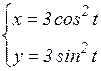
б) 
в) 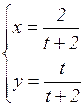
г) 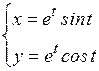
Занятие № 28.
Дифференциал и его применение в приближенных вычислениях.
Найти дифференциалы функций
а) 
б) 
в) 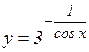
г) 
Найти приближенно изменение функции
а)  , а
, а  меняется от 100 до 101
меняется от 100 до 101
б)  , а
, а  меняется от
меняется от 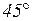 до
до 
в) 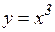 , а
, а  меняется от 2 до 1,98
меняется от 2 до 1,98
г)  , а
, а  меняется от
меняется от  до
до 
д)  , а
, а  меняется от 1 на 0,2
меняется от 1 на 0,2
Вычислить приближенно
а) 
б)  , если
, если 
в) 
г) 
д) 
е) 
ж) 
з) 
28.4. С какой точностью может быть вычислен объем шара, если его радиус измерен с точностью до 1%?
Занятие № 29.
Производные и дифференциалы высших порядков. Формула Тейлора.
29.1. Найдите производную 4-го порядка от функции 
Найдите производные 2-го порядка функций
а) 
б) 
в) 
Найти производные 2-го порядка от функций, заданных параметрически
а) 
б) 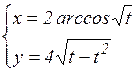
Найти производные n-го порядка функций
а) 
б) 
в) 
Найти вторые дифференциалы функций
а) 
б) 
в) 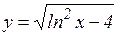
29.6. Найти третий дифференциал функции 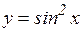
29.7. Разложить по формуле Тейлора (до степени не ниже 3-й) функции:
а) 
б) 
в) 
г) 
д) 
е) 
ж) 
з) 
и) 
к) 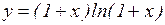
Вычислить приближенно с точностью до 0,0001
а) 
б) 
в) 
г) 
д) 
е) 
Занятие № 30.
Правило Лопиталя.
30.1. Используя правило Лопиталя, найти пределы:
а) 
б) 
в) 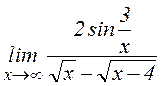
г) 
д) 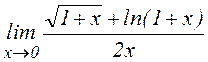
е) 
ж) 
з) 
и) 
к) 
30.2. Используя правило Лопиталя, найти пределы:
а) 

б) 
в) 

г) 
д) 
30.3. Используя правило Лопиталя, найти пределы:
а) 
б) 
в) 
г) 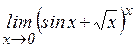
Занятие № 31.
Исследование функции на монотонность и экстремум
С помощью первой производной.
Найти интервалы монотонности и экстремумы функций
а) 
б) 
в) 
г) 
д) 
е) 
ж) 
з) 
и) 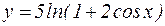
к) 
Найти наибольшее и наименьшее значение функций на заданных отрезках
а) 

б) 

в) 

г) 
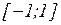
д) 

Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых являются квадратами, а каждая из боковых сторон имеет периметр, равный 6 см. Найти среди них параллелепипед с наибольшим объемом и найти этот объем.






