Приведение уравнений к каноническому виду.
14.1. Определить тип кривой второго порядка, составить ее каноническое уравнение:
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
.
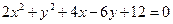14.2. Определить тип кривой приведением ее уравнения к каноническому виду методом Лагранжа:
1) 
;
2) 
;
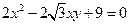3) 
;
4) 
;
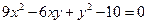5) 
.
14.3. Определить тип кривой методом инвариантов:
1) 
;
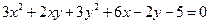2) 
;
3) 
;
4) 
;
5) 
.
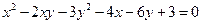14.4. Составить уравнение линии, сумма расстояний точек которой до точек А (2,4) и
В (-4,4) равна 8.
14.5. Составить уравнение линии, каждая точка которой вдвое дальше от прямой 
, чем от точки Р 
.
Занятие № 15.
Плоскость в пространстве.
15.1. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор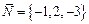 
15.2. Найти угол между плоскостями 
15.3. Написать уравнение плоскости, проходящей через точку 
перпендикулярно вектору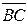 
: 
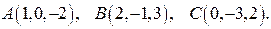
15.4. Найти уравнение плоскости, проходящей через точки А(5, 4, 1), В(4, -2, -1), С(0, 6, 5).
15.5. Составить уравнение плоскости, проходящей через точку Р 
параллельно двум векторам 
, 
.
15.6. Составить уравнение плоскости, проходящей через начало координат и перпендикулярной к плоскостям x +2y – 2z = 1, x – 2y + z = 4.
15.7. Найти расстояние от точки М(1,3,1) до плоскости 2x – y – 2z – 3 = 0.
15.8. Написать уравнение плоскости, проходящей через точку Р(3,-1,-2) и отсекающей на осях координат равные отрезки.
15.9. Написать уравнение плоскости, проходящей через точку M(1,0,2) и отсекающей на осях Ox и Oy отрезки a=2 и b=3.
15.10. Найти косинусы углов нормали плоскости 2x + y + 2z – 4 = 0 с осями координат.
15.11. Написать уравнение плоскости, проходящей через ось Oz и через точку А(2;1;-1). 15.12. Вычислить расстояние от точки (-1, 1, -2) до плоскости, проходящей через три точки А(1, -1, 1), В(-2, 1, 3), С(4, -5, -2).
15.13. Составить уравнения плоскостей, параллельных плоскости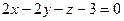 
и отстоящих от нее на расстояние d = 5.
15.14. Тетраэдр задан координатами своих вершин: 
. Составить уравнения плоскостей, проходящих через: а) вершину D, параллельно грани ABC; б) вершину В, параллельно грани ADC; в) ребро АС, параллельно ребру BD; г) ребро ВС, параллельно ребру AD.
15.15. Даны координаты четырех вершин параллелепипеда 
: 
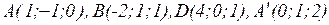. Составить уравнения плоскостей, проходящих через: а) ребро 
, параллельно диагонали 
; б) диагональ 
грани, параллельно диагонали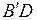 
; в) диагональ 
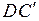грани, параллельно прямой 
.
Занятие № 16.
Прямая в пространстве.
16.1. Написать канонические уравнения прямой:
1) проходящей через две точки A(1,-1,3), B(2,1,-1),
2) проходящей через точку A(3,1,2) и параллельной вектору 
.
16.2. Найти косинус угла между прямыми:
и 
.
16.3. Найти расстояние точки M(2,-1,3) до прямой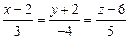 
.
16.4. Составить канонические уравнения прямой, проходящей через точку Р(2, -5, 3) и параллельной прямой 
.
16.5 Написать уравнения прямой 
в канонической и параметрической формах.
16.6. Даны вершины треугольника A(3,-1,-1), B(1,2,-7) и С(-5,14,-3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине B.
16.7. Составить уравнения прямой, которая проходит через точку А(-1,-3,2) и пересекает две прямые 
; 
.
16.8. Исследовать взаимное расположение прямых 
и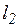 
. Если прямые пересекаются, то определить координаты их точки пересечения:
а) 
, 
;
б) 
, 
;
в) 
, 
;
г) 
, 
.
16.9. Доказать, что прямые и 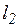пересекаются, и составить уравнение плоскости, которая их содержит:
а) 
, 
;
б)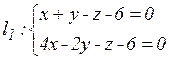 
, 
.
16.10. Доказать, что прямые и 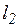скрещиваются. Составить уравнения плоскостей, каждая из которых содержит одну из этих прямых и параллельна второй:
а) 
, 
;
б) 
, 
.
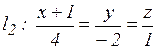16.11. Определить уравнение прямой, проходящей через точку М, пересекающей прямую 
и перпендикулярной к ней:)
а)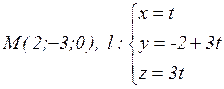 
; б)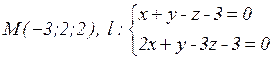 
.
16.12. Даны координаты вершин треугольника АВС. Составить уравнения его высот:
а) 
; б) 
.
Занятие № 17.
