 ?
?
Будет ли сходиться последовательность
 ?
?
21.3. Доказать, что последовательность  имеет предел, равный 0.
имеет предел, равный 0.
21.4. Доказать, что последовательность  сходится к
сходится к  .
.
21.5. Доказать, что последовательность  не имеет предела при
не имеет предела при  .
.
21.6. Доказать, что  .
.
21.7. Доказать, что  .
.
21.8. Имеет ли предел последовательность?
а)  ; б)
; б)  .
.
21.9. Последовательность 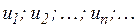 имеет предел
имеет предел  .
.
Доказать, что 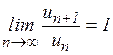 .
.
Что можно сказать об этом пределе, если  ? (Привести примеры).
? (Привести примеры).
21.10. Найти пределы:
а)  ; б)
; б) 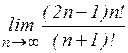 .
.
21.11. Найти пределы:
а)  ; б)
; б)  .
.
21.12. Доказать, что последовательность 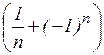 расходится.
расходится.
21.13. Доказать, что  .
.
21.13. Найти  .
.
21.14. Доказать, что при  справедливо равенство
справедливо равенство  .
.
21.15. Доказать, что  .
.
21.16. Доказать, что при  справедливо равенство
справедливо равенство  .
.
21.17. Доказать, что при  справедливо равенство
справедливо равенство
Занятие № 22.
Вычисление пределов функций с помощью определения и свойств пределов.
22.1. Доказать, что  .
.
22.2 Доказать, что  .
.
22.3. Найти пределы:
а)  ; б)
; б)  ; в)
; в)  .
.
22.4. Найти пределы:
а)  ; б)
; б) 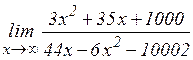 ;
;
в)  ; г)
; г)  .
.
22.5. Найти пределы:
а)  ; б)
; б)  ; в)
; в) 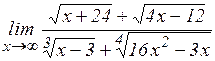 ;
;
г)  ; д)
; д) 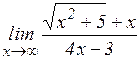 ; е)
; е)  .
.
22.6. Найти пределы:
а)  ; б)
; б)  ; в)
; в)  .
.
Занятие № 23.
Вычисление пределов функций с помощью алгебраических преобразований.
23.1. Найти пределы рациональных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е) 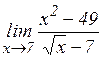 ; ж)
; ж)  ; з)
; з)  .
.
23.2. Найти пределы иррациональных дробей:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ,
,
23.3. Найти пределы в бесконечно удаленных точках:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 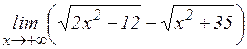 ;
;
ж) 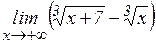 ; з)
; з)  .
.
Занятие № 24.
Замечательные пределы. Бесконечно малые и бесконечно большие функции.
24.1. С применением первого замечательного предела, вычислить:
а)  ; б)
; б)  ; в)
; в) 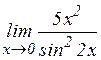 ; г)
; г) 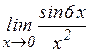 ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и)  ; к)
; к)  ; л)
; л)  ; м)
; м) 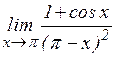 .
.
24.2. С применением второго замечательного предела вычислить:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 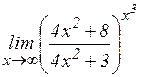 ; е)
; е)  ; ж)
; ж)  .
.
24.3. С применением третьего замечательно предела, вычислить:
а) 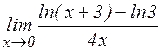 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Занятие № 25.
Вычисление пределов с помощью эквивалентных функций.
Найти пределы:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ;
;
з) 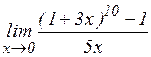 ; и)
; и)  ; к)
; к) 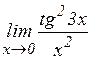 ;
;
л)  ; м)
; м)  .
.
Занятие № 26.
Непрерывность функций и точки разрыва.
26.1. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.2. Исследовать на непрерывность функцию 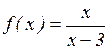 . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.3. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.4. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.5. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.6. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
26.7. Исследовать на непрерывность функцию  . В случае разрыва указать его характер.
. В случае разрыва указать его характер.
Дифференциальное исчисление функций одной переменной.
Занятие № 27.
Дифференцирование функций. Геометрический смысл производной.
27.1. Используя определение производной, найти производные следующих функций:
а) 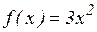 ; б)
; б)  ; в)
; в) 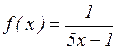 .
.
27.2. Используя правила дифференцирования, найти производные следующих функций:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж)  ;
;
з) 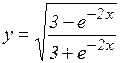 ;
;
и) 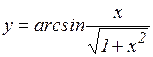 ;
;
к)  .
.






