31.5. Требуется огородить два участка: один – в форме правильного треугольника, другой – в форме полукруга. Длина изгороди фиксирована и равна Р. Определить размеры участков (строну треугольника и радиус полукруга) так, чтобы сумма площадей этих участков была бы наибольшей.
31.6. В треугольнике с основанием а и радиусом h вписан прямоугольник, основание которого лежит на основании треугольника, а две вершины – на боковых сторонах. Найти наибольшую площадь вписанного прямоугольника.
Занятие № 32.
Исследование функции на выпуклость и наличие точек перегиба
С помощью производной второго порядка.
Найти точки перегиба и интервалы выпуклости функций
а) 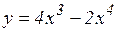
б) 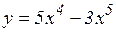
в) 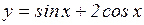
г) 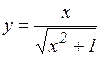
д) 
е) 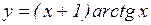
ж) 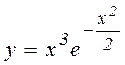
з) 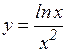
и) 
к) 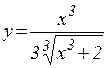
Занятие № 33.
Асимптоты графиков функций.
Найти асимптоты графиков функций
а) 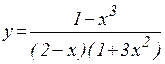
б) 
в) 
г) 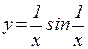
д) 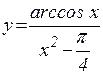
е) 
ж) 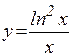
з) 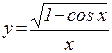
Занятие № 34.
Общая схема исследования функций и построения графиков.
Исследовать функции и построить их графики
а) 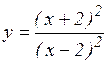
б) 
в) 
г) 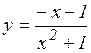
д) 
е) 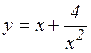
ж) 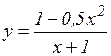
з) 
и) 
к) 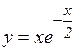
л) 
м) 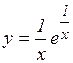
Исследовать функции и построить их графики
а) 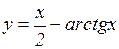
б) 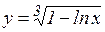
в) 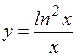
г) 
д) 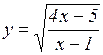
е) 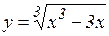
ж) 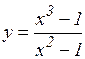
з) 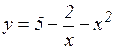
и) 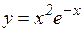
к) 
л) 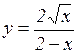
м) 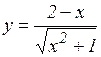
Интегральное исчисление функций одной переменной.
Занятие № 35.
Интегрирование заменой переменной.
35.1. Найдите неопределенные интегралы:
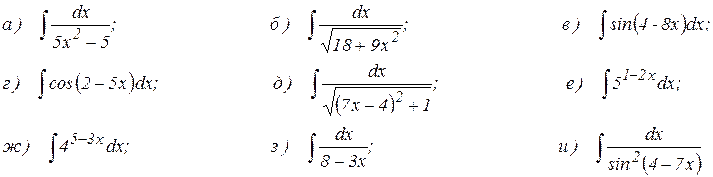
35.2. Найдите неопределенные интегралы:

Занятие № 36.
Интегрирование по частям.
36.1. Найдите неопределенные интегралы:
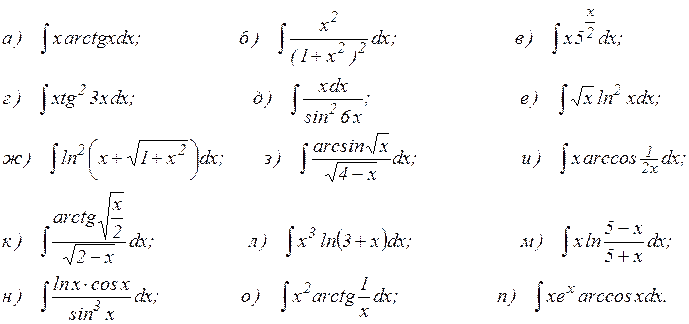
Занятие № 37.
Интегрирование рациональных функций.
37.1. Найдите неопределенные интегралы: 

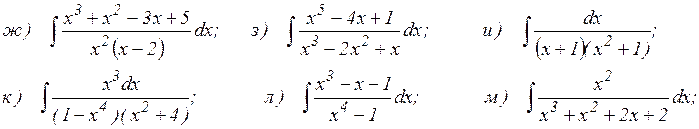
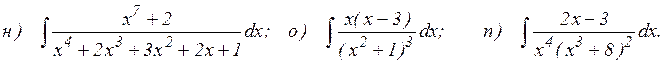
Занятие № 38.
Интегрирование иррациональных функций.
38.1. Найдите неопределенные интегралы:
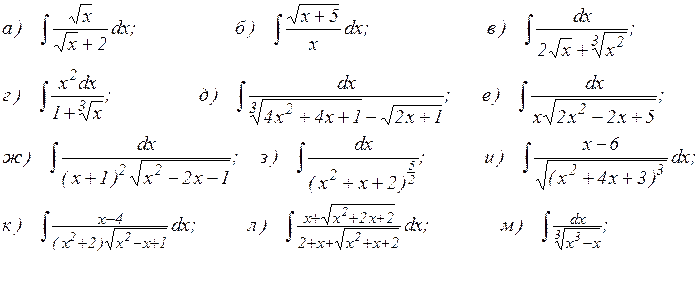
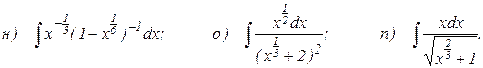
Занятие № 39.
Интегрирование тригонометрических функций.
39.1. Найдите неопределенные интегралы:


Занятие № 40.
Определенный интеграл. Вычисление длин дуг кривых.
40.1. Вычислить определенный интеграл как предел интегральной суммы:
а) 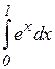 ; б)
; б) 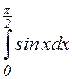 ; в)
; в) 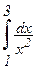 .
.
40.2. С помощью формулы Ньютона-Лейбница вычислить определенные интегралы:
а) 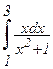 ; б)
; б) 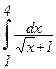 ; в)
; в) 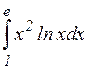 ;
;
40.3. Вычислите длину дуги кривой:


Занятие № 41.
Вычисление площадей плоских фигур.
41.1. Вычислите площадь фигуры, ограниченной линиями, заданными уравнениями в декартовых или полярных координатах: 

Занятие № 42.
Вычисление объемов тел вращения.
42.1. Вычислите объем тела, образованного вращением вокруг указанной оси координат фигуры, ограниченной заданными линиями:
а)  вокруг оси Оx;
вокруг оси Оx;
б) 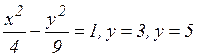 вокруг оси Оy;
вокруг оси Оy;
в) 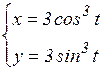 вокруг оси Оx;
вокруг оси Оx;
г) 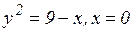 вокруг оси Оy;
вокруг оси Оy;
д)  ;
;
е)  ;
;
ж) 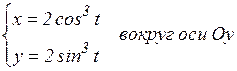 .
.
Занятие № 43.
Несобственные интегралы на бесконечных промежутках.
43.1. Вычислить несобственные интегралы или доказать их расходимость:


Занятие № 44.
Несобственные интегралы от неограниченных функций.
44.1. Вычислить интегралы или установить их расходимость:
а)  ; б)
; б) 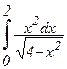 ; в)
; в) 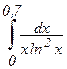 ; г)
; г) 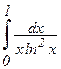 ; д)
; д)  ;
;
е) 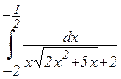 ; ж)
; ж)  ; з)
; з) 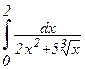 ; и)
; и) 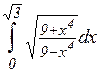 ;
;
к) 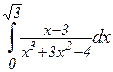 ; л)
; л)  ; м)
; м) 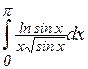 ; н)
; н) 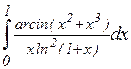 ;
;
о) 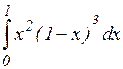 ; п)
; п) 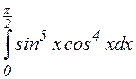 ; р)
; р)  .
.
Дифференциальное исчисление функций нескольких переменных.
Занятие № 45.




