1) Алгебраическая форма z = x + iy
2) Тригонометрическая форма 
Действительное число r =  называется модулем комплексного числа
называется модулем комплексного числа
z = x + iy. Геометрически модуль числа z - длина радиуса вектора точки z;
Угол  называется аргументом комплексного числа z и обозначается
называется аргументом комплексного числа z и обозначается 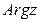 :
:  , где φ = argz -главное значение аргумента комплексного числа;
, где φ = argz -главное значение аргумента комплексного числа; 

3) Показательная форма комплексного числа 
 - уравнение окружности радиуса R с центром в точке z 0.
- уравнение окружности радиуса R с центром в точке z 0.
Задания
1). Найдите действительную часть комплексного числа z = 4+2i; z = 6;
z = -7i;  ;
; 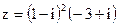
Изобразите области
2). Где расположены точки  , для которых;
, для которых;  ;
;  ;
;  ;
; 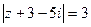 ?
?
3). 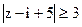 ; 4).
; 4). 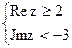 ; 5).
; 5).  ; 6).
; 6).  ;
;
Представить в тригонометрической и показательной формах число
7).  ; 8).
; 8).  ; 9).
; 9).  ; 10).
; 10). 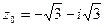 ; 11).
; 11).  .
.
II. Функция комплексного переменного
Определение: Комплексная переменная величина W называется функцией комплексной величины Z, если каждому значению, которое может принимать величина Z, соответствует определенное комплексное числовое значение W = u + iv, те w = f(z).
Различают однозначные функции и многозначные
Определение:
Если каждому z 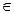 D соответствует одно значение w, то функция w = f(z) называется однозначной. Если каждому z
D соответствует одно значение w, то функция w = f(z) называется однозначной. Если каждому z 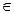 D соответствует несколько значений w, то функция w = f(z) называется многозначной.
D соответствует несколько значений w, то функция w = f(z) называется многозначной.
Необходимым и достаточным условием дифференцируемости функции  в точке
в точке  являются непрерывность в этой точке частных производных 1-го порядка функций
являются непрерывность в этой точке частных производных 1-го порядка функций  и
и  по обеим переменным и выполнение равенств
по обеим переменным и выполнение равенств
 ,
, 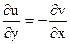
Определение: Функция w = f(x), дифференцируемая в каждой точке некоторой области D, называется аналитической в этой области
Исследовать на аналитичность
12).  ; 13).
; 13).  ; 14).
; 14).  ; 15).
; 15). 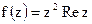 ;
;
Найти аналитическую функцию по заданной действительной или мнимой части
16).  17).
17). 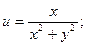
18). 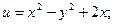 19).
19). 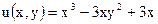 и
и 
20). 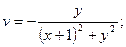 21).
21). 
III. Элементарные функции комплексного переменного
1. Степенная функция:  , где
, где  .
.
а) 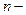 натуральное число, тогда
натуральное число, тогда  .
.
б)  , где
, где 

 , где
, где 
Функция многозначная (q – значная) Однозначная ветвь этой функции получается, если придать к определенное значение
в)  , где
, где 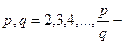 несократимая дробь.
несократимая дробь.
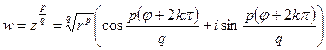 , где
, где 
2. Показательная функция:
 , где
, где  определяется равенством
определяется равенством 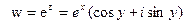
3. Логарифмическая функциия:
Lnz = ln  ;
;

4. Тригонометрические функции:
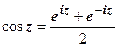 ,
, 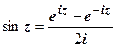 ,
, 

5. Гиперболические функции:
 ,
, 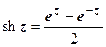 ,
,  ,
,  .
.
 ;
;  - формулы связи между тригонометрическими и гиперболическими функциями
- формулы связи между тригонометрическими и гиперболическими функциями
6. Обобщенная показательная функция w =  и обобщенная степенная w =
и обобщенная степенная w = 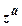 (а, z - произвольные комплексные числа,
(а, z - произвольные комплексные числа, 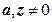 ) функции определяются соотношениями
) функции определяются соотношениями  .
.
22). Вычислить а)  ; б)
; б)  ; 23). Решить уравнение
; 23). Решить уравнение  .
.
24). Найти 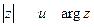
а) z = 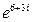 , б) z =
, б) z =  , в) z =
, в) z =  , г) z =
, г) z =  .
.
25). Вычислить а) Ln(4); б) Ln(-1); в)  ; г)
; г)  .
.
Найти действительную и мнимую часть выражения:
26). а)  ; б) sin2i; в) cos(2 + i); г) tg(2-i);
; б) sin2i; в) cos(2 + i); г) tg(2-i);
27). Вычислить а)  б )
б ) 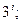 в)
в)  г)
г)  .
.






