Миндерова О. Н.
Сборник упражнений по высшей математике
Дифференциальные уравнения
Системы дифференциальных уравнений
Элементы теории поля
Ряды
ТФКП
Операционные исчисления
III семестр
Классы ___121,122_________
Прежде чем приступить к решению упражнений,
Выучи теорию,
Используя литературу и лекции по ВМ.
Без знания теории практика бессмысленна!!!!
Данный сборник не является источником теоретического материала, предназначен только для практических занятий.
2012-2013
Тема № 1 Дифференциальные уравнения
I. Дифференциальные уравнения первого порядка
Литература по теме:
1.Мачехина, Ильенок «ДУ первого порядка»
2. Письменный «Конспект лекций по высшей математике» кн 2
3. Пискунов «Дифференциальные и интегральные исчисления», т 2
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции.
Решением или интегралом д/у называется любая функция, подстановка которой в уравнение обращает его в тождество
Процесс нахождения решения д/у называется интегрированием
Уравнения с разделяющимися переменными
Определение: Дифференциальное уравнение вида
 (1)
(1)
называется уравнением с разделяющимися переменными
Или
 (2)
(2)
Метод решения: (1)
1. Разделяем переменные, перенося слагаемые в разные стороны, получим уравнение 

2. Почленно делим обе части уравнения на  , получаем уравнение с разделенными переменными
, получаем уравнение с разделенными переменными 
3. Интегрируя обе части уравнения, получаем общее решение или интеграл исходного уравнения
4. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Метод решения: (2)
1. Подставляем  , затем приводим уравнение к форме (1) и используем метод решения рассмотренный ранее
, затем приводим уравнение к форме (1) и используем метод решения рассмотренный ранее
Найти общее решение или общий интеграл уравнения
№1 ◦.  №2 ◦.
№2 ◦.  .
.
№3 ◦. y’ = cos(2x + 5) №4 ◦. 
№5 ◦.  №6 ◦.
№6 ◦. 
№7 ◦.  ;
;  №8 ◦.
№8 ◦.  ,
, 
№9 ◦.  ;
;  №10.
№10.  ;
;  .
.
№11•.  №12•.
№12•. 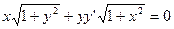
№13•. №16•.  №14•
№14•  ;
;  №15•. •
№15•. •  ;
; 
Однородные уравнения
Определение: Уравнение вида  является однородным, если функции P(x, y) и Q(x, y) – однородные функции одного измерения.
является однородным, если функции P(x, y) и Q(x, y) – однородные функции одного измерения.
Уравнение  - однородное, если функция f(x, y) – однородная нулевого измерения.
- однородное, если функция f(x, y) – однородная нулевого измерения.
Метод решения
1. Вводим новую переменную 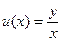 , где
, где  - дифференцируемая функция
- дифференцируемая функция
2. Находим  ;
; 
3. Получаем д/у с разделяющими переменными относительно функции u(x), решив его делаем обратную замену 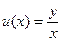
Найти общее решение или общий интеграл уравнения
№16 ◦..  ;
;  №17 ◦.
№17 ◦.  .
.
№18 ◦..  №19 ◦.
№19 ◦. 
№20 ◦.  №21 ◦.
№21 ◦. 
№22 ◦.  №23 ◦.
№23 ◦. 

№24•.  . №25•.
. №25•. 
№26•  . №27•.
. №27•.  ;
;  .
.
№28•  ;
;  . №29•.
. №29•. 
Линейные уравнения
Определение. Дифференциальное уравнение вида

P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b., в частности константы, называется линейным
Решение линейного уравнения ищем в виде  , где u(x) и v(x) – дифференцируемые функции и
, где u(x) и v(x) – дифференцируемые функции и 
Найти общее решение или общий интеграл уравнения
№30 ◦  . №31 ◦.
. №31 ◦. 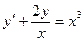
№32 ◦.  №33 ◦.
№33 ◦. 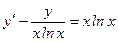
№34 ◦.  №35 ◦.
№35 ◦. 
№36 ◦.  ,
,  . №37•.
. №37•. 
Уравнения Бернулли
Определение. Уравнением Бернулли называется уравнение вида

где P и Q – функции от х в частности константы, а n 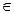 R, n
R, n  0 и n
0 и n  1.
1.
Решение уравнения Бернулли ищем в виде  , где
, где 
№38 ◦.  №39 ◦.
№39 ◦. 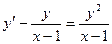
№40•.  №41 ◦.
№41 ◦. 
№42•.  №43 ◦.
№43 ◦. 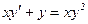
№44 ◦.  №45•.
№45•. 






