Определение. Дифференциальное уравнение первого порядка вида:

называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 
 ,
,
тк du(x) =0, то u(x) = C - это есть общий интеграл заданного д/у
Формы нахождения u(x,y) по ее полному дифференциалу:
1) 
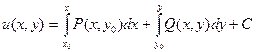 или
или 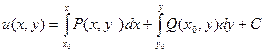
где ( ) – любая фиксированная точка, входящая в область определения функций P(x,y) и Q(x,y)
) – любая фиксированная точка, входящая в область определения функций P(x,y) и Q(x,y)
Найти общее решение или общий интеграл уравнения
№46 ◦.  . №47 ◦.
. №47 ◦.  .
.
№48 ◦.  . №49 ◦.
. №49 ◦.  .
.
№50 ◦.  . №51.
. №51.  .
.
№52•  ;
;  . №53•.
. №53•.  ;
;  .
.
I.Вопросы по теме
«Дифференциальные уравнения первого порядка»
1. Что называется уравнением?
2. Что является решением любого уравнения?
3. Что называется дифференциальным уравнением первого порядка?
4. Что называется решением ДУ?
5. В каком случае ДУ называется обыкновенным? В частных производных?
6. Что определяет порядок ДУ?
7. Что значит решить ДУ?
8. Как называется процесс нахождения решения ДУ?
9. Что является графиком решения ДУ
10. Общий вид ДУ первого порядка
11. ДУ первого порядка, разрешенное относительно производной
12. Что называется общим решением (общим интегралом) ДУ?
13. Что называется частным решением (частным интегралом)ДУ?
14. В чем заключается задача Коши?
15. Теорема существования и единственности решения задачи Коши
I. Знать с доказательством:
1. Определение, формы записи, метод решения уравнений типа:
а) с разделяющимися переменными;
б) однородные I порядка;
в) линейные I порядка;
г) в полных дифференциалах.
II. Дифференциальные уравнения высших порядков
Литература по теме:
1.Ильенок, Бажанова «ДУ высших порядков»
2. Письменный «Конспект лекций по высшей математике» кн 2
3. Пискунов «Дифференциальные и интегральные исчисления», т 2
Уравнения, допускающие понижение порядка
| № | Общий вид | Метод решения |

| Интегрируем столько раз, каков порядок уравнения | |
 ; ; 
| Замена: 
| |
 ; ; 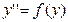
| Замена: 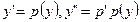
|
а) Уравнение вида 
Решить уравнения
№54 ◦.  №55 ◦.
№55 ◦. 
№56•.  ,если при
,если при  ,
, 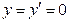 .
.
№57•.  , если при
, если при 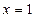 ,
,  ,
, 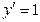 ,
,  .
.
№58•.  , ели при
, ели при  ,
,  ,
, 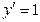 .
.
№59•.  , если при
, если при  ,
,  ,
, 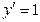 .
.
№60•.  , если при
, если при  ,
,  ,
, 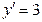 .
.
б) Уравнение вида 
№61 ◦.  . №62 ◦.
. №62 ◦.  .
.
№63 ◦ 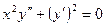 . №64•
. №64•  .
.
№65•.  , если при
, если при 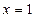 ,
, 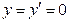 .
.
№66•.  , если при
, если при 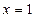 ,
,  .
.
№67•.  , ели при
, ели при  ,
,  ,
, 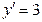 .
.
в) Уравнение вида 
№68 ◦.  , считая
, считая  №69 ◦.
№69 ◦.  .
.
№70 ◦.  . №71•.
. №71•.  .
.
№72•. 
ЛОДУ с постоянными коэффициентами
Корни характеристического уравнения 
| 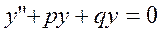
| |
| Частные решения (ФСР) | Общее решение | |

| 
| 
|

| 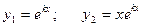
| 
|

| 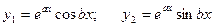
| 
|
Решить уравнения
№73 ◦. 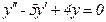 . №74 ◦.
. №74 ◦.  .
.
№75 ◦.  . №76 ◦.
. №76 ◦.  .
.
№77 ◦.  . №78 ◦.
. №78 ◦.  .
.
№79 ◦  . №80 ◦.
. №80 ◦.  .
.
№81 ◦. 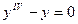 . №82 ◦.
. №82 ◦.  .
.
№83•.  , если при
, если при  ,
,  ,
,  .
.
№84•  , если при
, если при  ,
,  ,
,  .
.
№85•  , если при
, если при  ,
,  ,
,  .
.
Линейные неоднородные ДУ.
Решить ЛНДУ 2-го порядка с постоянными коэффициентами
а). ЛНДУ вида 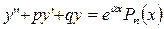
Общий вид 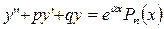
|
Общее решение  + + 
|
где  - решение соответствующего однородного уравнения - решение соответствующего однородного уравнения 
|
 , где , где  - из условия; - из условия;
 и и  - многочлены n – степени, n ϵ Z - многочлены n – степени, n ϵ Z
|
 - кратность корня:если - кратность корня:если  , то , то  = 0;
если = 0;
если 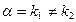 , то , то  = 1;
если = 1;
если  , то , то  = 2. = 2.
|
Замечание: если n = 0, то  =
=  ; если n = 1, то
; если n = 1, то  =
=  ;
;
если n = 2, то  =
=  ;
;
№86.  . №87.
. №87. 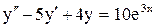 .
.
№88.  . №89.
. №89.  .
.
№90.  . №91.
. №91.  .
.
№92. 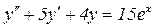 .
.
№93.  если при
если при  ,
,  .
.
Б). ЛНДУ вида

Общий вид 
|
Общее решение + + 
|
где  - общее решение соответствующего однородного уравнения - общее решение соответствующего однородного уравнения 
|
y* - частное решение ЛНДУ
 ,
где ,
где  - из условия - из условия
 , ,  - многочлены степени l, l = - многочлены степени l, l =  , n,m ϵ Z , n,m ϵ Z
|
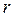 - кратность корня:
если - кратность корня:
если  , то , то 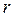 = 0;
если = 0;
если 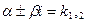 , то , то  = 1
где k1,2 – корни соответствующего характеристического уравнения. = 1
где k1,2 – корни соответствующего характеристического уравнения.
|
№94.  . №95.
. №95.  .
.
№96. 
№97.  , если при
, если при 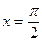 ,
,  .
.
№98.  , если при
, если при  ,
,  .
.
№99. 
Метод Лагранжа




