Правило интегрирования ЛНДУ методом Лагранжа

1. Находим решение соответствующего ЛОДУ в виде

2. Устанавливает ожидаемый вид ,

3. Составляем СЛАУ

4. Находим решение СЛАУ

5. Интегрируем и находим

6. Записываем общее решение

Решить ЛНДУ методом Лагранжа

№100. .

№101. . №102. .

№103. . №104. .

№105. №106. .

№107. 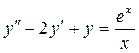. №108. .

 

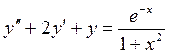II. Вопросы по теме:

«Дифференциальные уравнения второго и высших порядков»

 

1. Какое уравнения называется ДУ высшего порядка?

2. Формы записи обыкновенного ДУ второго (n- го) порядка

3. Что называется решением ДУ n – порядка?

4. Как называется график решения ДУ?

5. Что значит «решить ДУ n – порядка»?

6. Что называется общим решением ДУ второго (n- го) порядка?

7. Что называется частным решением ДУ второго (n- го) порядка?

8. Что называется общим интегралом ДУ второго (n- го) порядка?

9. Что называется частным интегралом ДУ второго (n- го) порядка?

10. В чем заключается задача Коши для ДУ второго (n- го) порядка?

11. Теорема существования и единственности решения задачи Коши для второго (n- го) порядка?

Общий вид ДУ допускающих понижение степени и методы их решения

13. Определение линейного дифференциального уравнения n – го порядка. Виды ЛДУ.

14. Линейные однородные дифференциальные уравнения (ЛОДУ)

Теорема о частных решения ЛОДУ второго порядка

16. Определение линейно независимых и линейно зависимых частных решений ЛОДУ

Определение ФСР и ее свойства (основные теоремы)

Теорема о структуре общего решения ЛОДУ второго (n- порядка) порядка.

19. ЛОДУ второго и высших порядков с постоянными коэффициентами, основные определения.

20. Общий вид частных и общего решения ЛОДУ второго порядка с постоянными коэффициентами в случае: а)действительных и различных; б) действительных и равных; в) комплексно сопряженных корней характеристического уравнения.

21. Сформулируйте правило интегрирования ЛОДУ n- порядка с постоянными коэффициентами.

22. ЛНДУ. Общий вид ЛНДУ второго (n- го) порядка.

23. Теорема о структуре общего решения ЛНДУ n – порядка

24. ЛНДУ второго порядка с постоянными коэффициентами

25. В чем сущность метода неопределенных коэффициентов? Для какого типа уравнений он применяется?

26. Специальные виды правой части ЛНДУ с постоянными коэффициентами.

27. Ожидаемая форма частного решения y* ЛНДУ с постоянными коэффициентами, если f(x) имеет первый или второй специальный вид

Теорема о наложении частных решений.

29. Теорема о структуре общего решения ЛНДУ

30. В чем состоит метод вариации произвольных постоянных?

При интегрировании каких дифференциальных уравнений целесообразно применять этот метод?

 

III.Системы дифференциальных уравнений

Литература по теме

1. Письменный «Конспект лекций по высшей математике» кн 2

2. Пискунов «Дифференциальные и интегральные исчисления», т 2