РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 8

Тема: «Изгиб прямого бруса»

Цель работы:

Расчеты балок на прочность по нормальным и касательным напряжениям. Подбор поперечного сечения балки

Студент должен

знать:

-формулы, по которым определяются нормальные и касательные напряжения при изгибе;

-эпюры нормальных и касательных напряжений по высоте сечения балки и практический смысл этих эпюр;

- условия прочности при изгибе.

уметь:

- рассчитывать балки на прочность и производить подбор сечения балки;

- выполнять расчеты балок на прочность.

Вопросы для самоконтроля:

1. Что называется прочностью сечения?
2. По какой формуле определяется нормальное напряжение в поперечном сечении балки при изгибе?
3. Изменяются ли нормальные напряжения при изгибе по высоте сечения балки?
4. Что называется осевым моментом сопротивления сечения?
5. Каковы единицы измерения момента сопротивления?
6. По какой формуле определяется касательное напряжение при изгибе?
7. Чему равны касательные напряжения при изгибе в крайних волокнах балки?
8. Чему равны максимальные касательные при изгибе в двутавровом сечении?
9. Как производится расчет балки на прочность?

 

Методические указания

 

1. Построить эпюры Q_х и М_х.

2. Подобрать сечение стальной балки в следующем порядке:

а) определяют требуемый момент сопротивления сечения балки:

,

где М_max — наибольший по абсолютному значению изгибающий момент, принимаемый по эпюре М_х;

R — расчетное сопротивление материала по пределу текучести,

m – коэффициент условий работы;

б) по ГОСТам прил. 1 подбирают номер двутавровой стальной балки, которая должна иметь момент сопротивления W_x наиболее близкий по значению к требуемому моменту сопротивления W .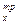

3. Определить максимальные и минимальные нормальные напряжения (на растяжение и сжатие) по формуле

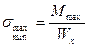
где W_х — момент сопротивления относительно нейтральной оси принятого двутаврового сечения.

4. Построить эпюру нормальных напряжений 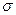. Для этого вычерчивают крупно поперечное сечение балки и проводят на отдельном рисунке основную линию перпендикулярно нейтральной оси. Затем на уровне крайних точек сечения (верхней и нижней) откладывают найденные ранее значения и и соединяют эти значения прямой линией. Полученный график называется эпюрой 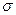. Значения и откладывают по разные стороны от нулевой линии (на растяжение – вправо от основной линии, на сжатие - влево).

5. Проверить прочность принятой двутавровой балки по касательным напряжениям. Наибольшие касательные напряжения возникают в том сечении по длине балки, в котором действует наибольшая поперечная сила (по абсолютному значению), а по высоте сечения — на уровне нейтрального слоя.

Касательные напряжения на уровне нейтрального слоя определяют по формуле Журавского:

,

 

где Q _X — максимальная поперечная сила в рассматриваемом сечении балки;

S _x— статический момент сечения, расположенного выше или ниже нейтральной оси (выбирается по сортаменту);

J _x — момент инерции всего сечения, принимается по сортаменту;

b — ширина сечения балки на уровне нейтрального слоя (для двутавра выбирается по сортаменту, размер «d»).

6. Построить эпюру касательных напряжений. Касательные напряжения изменяются по высоте балки по криволинейному закону и имеют скачок в месте соединения полки и стенки. Поэтому эпюру 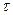строят по значениям, найденным в пяти точках сечения: крайних точках, на уровне нейтральной оси и на уровне сопряжения стенки и полки — чуть ниже и чуть выше этого сопряжения.

Напряжение в этих точках определяется по формуле Журавского. При этом статический момент S _х и ширина сечения b определяются для каждой точки сечения. Касательные напряжения в крайних точках сечения равны нулю.

Пример 1. Для балки построить эпюры поперечных сил и изгибающих моментов. Определить момент сопротивления. Подобрать сечение стальной двутавровой балки (рис. а). Для выбранного двутавра построить эпюры нормальных и касательных напряжений. Материал — сталь марки С-235, m = 1.

Решение

1. Построить эпюры Q_у, М_х (см. пример расчетно-графической работы № 7). Наибольшее значение поперечной силы Q_max = 73,6 кН, изгибающего момента

М_max = 95,4 кН×м (см. рис. 21).

2. Подобрать сечение стальной двутавровой балки по наибольшему изгибающему моменту

= 415 см³,

где R = 230 МПа — расчетное сопротивление стали марки С-235.

По сортаменту принимаем двутавровую балку № 30 с W _х = 472 см³, что больше, чем расчетный момент сопротивления W 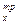= 415 см³.

3. Проверить прочность принятого сечения:

< R = 230 МПа.

Прочность сечения по нормальным напряжениям обеспечена.

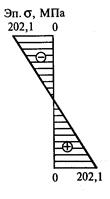
4. Построить эпюру нормальных напряжений. Отложим от нулевой линии 0—0 (рис. 22, б) значение 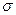_max = 202,1 МПа и 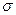_min = 202,1 МПа и соединим полученные точки. Верхняя часть испытывает сжатие, нижняя — растяжение, так как по эпюре М_х видно, что балка прогибается (обращена выпуклостью) вниз.

5. Проверить прочность балки по касательным напряжениям. Заменим действительное сечение упрощенным (рис. 22, в). Размеры d = 6,5 мм; b = 135 мм приняты по сортаменту.

Определим наибольшее касательное напряжение

а б в

рис. 22

где = 73,6 МН;

см³ = 263 м³;

J_х = 7080 см⁴ = 7080 м⁴;

d = 6,5 мм = 6,5 м.

Подставим числовые значения в формулу для (сечение 1—1):

= МПа

Проверим прочность сечения по касательным напряжениям:

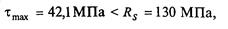
т. е. прочность обеспечена.

В прокатных балках, которые не несут больших сосредоточенных сил в приопорных участках, это условие обычно соблюдается с большим запасом.

 

6. Построить эпюру .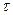

По найденным значениям строим эпюру 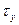(рис. 22, в).

Задание для расчетно-графической работы 8. Для стальной балки подобрать поперечное сечение из двутавра. Проверить принятое сечение по нормальным (для сечения с наибольшим изгибающим моментом) и по касательным (для сечения с наибольшей поперечной силой) напряжениям и построить эпюры 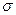и 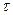для соответствующих сечений. Материал — сталь С-245. Исходные данные взять из расчетно-графической работы № 2 (задача 2) по теоретической механике.