Тема: «Центр тяжести тела»
Цель работы:
Определение положения центра тяжести сложных плоских фигур, имеющих одну ось симметрии, составленных из простых геометрических фигур и из стандартных прокатных профилей
Студент должен знать:
- статические моменты плоской фигуры;
- формулы для определения координат центра тяжести плоских фигур.
Студент должен уметь:
- определять координаты центра тяжести плоских фигур;
- определять координаты центра тяжести стандартных прокатных профилей.
Вопросы для самоконтроля:
- Что называется центром тяжести тела?
- Записать формулы для определения координат центра параллельных сил.
- Записать формулы для определения координат центра тяжести тонкой однородной пластины.
- Что называется статическим моментом площади плоской фигуры относительно оси? В каком случае он равен нулю?
- Как определить координаты центров тяжести простых геометрических фигур, их площади?
- Как определить координаты центров тяжести стандартных прокатных профилей, их площади?
- Как определить положение центра тяжести плоской фигуры сложной формы?
Методические указания
1. Разбить сечение на простые фигуры. Такими фигурами являются стандартные профили проката, размеры которых приведены в прил. 1. Обычно профили прокатной стали, образующие сечение, обозначают цифрами 1, 2, 3… или простые геометрические фигуры – прямоугольники, квадраты, треугольники, круги.
2. Указать центры тяжести каждого профиля (фигуры) и обозначают их С1, С2,..., Сn, используя при необходимости таблицы ГОСТов (см. прил. 1).
3. Выбрать систему координатных осей. В задачах все сечения имеют одну ось симметрии, поэтому рекомендуется одну из координатных осей совмещать с ней. Вторую ось координат направляют перпендикулярно первой так, чтобы она пересекла центры тяжести одной или нескольких фигур. При этом начало координат может совпадать (или не совпадать) с центром тяжести одной из фигур. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точку сечения. В первом случае вычисления будут более простыми.
4. Составить формулы для определения координат центра тяжести сечения:

Пользуясь таблицами ГОСТов (см. прил. 1), определяют площади профилей проката А1, А2,..., Аn, координаты их центров тяжести х1, х2,..., хn и y1, у2,..., уn относительно выбранных осей координат. Число слагаемых в числителе и знаменателе формул зависит от числа профилей, из которых состоит сечение. Полученные величины подставляют в формулу и находят хс и ус. Аналогично ведется расчет площадей простых геометрических фигур, только по формулам.
Следует помнить, что если ось х совмещена с осью симметрии, то координата ус = О, а если ось у совмещена с осью сим метрии, то хс = 0.
5. Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба, и показывают расстояние от центра тяжести до координатных осей.
Пример 1, а. Определить координаты центра тяжести сечения, показанного на рис. 9. Сечение состоит из двух уголков 56  4 и швеллера №18. Указать его положение на сечении.
4 и швеллера №18. Указать его положение на сечении.
Решение
1. Разбить сечение на профили проката: два уголка 56  4 и швеллер №18. Обозначим их 1, 2, 3 (см. рис. 9).
4 и швеллер №18. Обозначим их 1, 2, 3 (см. рис. 9).
2. Указать центры тяжести каждого профиля, используяприл. 1, и обозначим их С1, С2, С3.
3. Выбрать систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков.
4. Определить координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому хс = 0. Координату ус определим по формуле

Пользуясь таблицами прил. 1, определим площади каждого профиля и координаты центров тяжести:
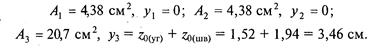
Координаты у1 и у2 равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения ус:


рис. 9
5. Указать центр тяжести сечения на рис. 9 и обозначить его буквой С. Показать расстояние ус от оси х до точки С.
Поскольку уголки симметрично расположены, имеют одинаковую площадь и координаты, то А1 = А2, у1 = у2. Поэтому формула для определения ус может быть упрощена:
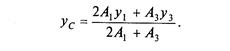
По найденным координатам хс и ус наносим на рисунок точку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами Ус, найденными при первом и втором решении, составляет: 6,51 — 2,43 = 4,08 см.
Это равно расстоянию между осями х при первом и втором решении: 5,6 — 1,52 = 4,08 см.
Ответ: ус = 2,43 см, если ось х проходит через центры тяжести уголков, или ус = 6,51 см, если ось х проходит по нижнему краю полки уголка.
Пример 1, б. Определить координаты центра тяжести сечения, изображенного на рис. 10. Сечение состоит из двутавра (I) № 24 и швеллера № 24 а. Показать положение центра тяжести на сечении.

рис. 10
Решение
1. Разбить сечение на профили проката: двутавр и швеллер. Обозначим их цифрами 1 и 2.
2. Указать центры тяжести каждого профиля С1 и С2, используя таблицы прил. 1..
3. Выбрать систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра.
4. Определить координаты центра тяжести сечения. Координата ус = 0, так как ось х совпадает с осью симметрии. Координату хс определим по формуле

По таблицам прил. 1 и схеме сечения определим

Подставим числовые значения в формулу и получим

5. Нанести точку С (центр тяжести сечения) по найденным значениям хс и ус (см. рис. 10).
Ответ: хс = 6,11 см, если ось у проходит через центр тяжести двутавра; хс = 11,86 см, если ось у проходит через левые крайние точки двутавра.
Пример 2. Определить центр тяжести сечения, составленного из простых геометрических фигур (рис. 11).



рис. 11
Решение
1. Вычертить схему в масштабе с указанием всех размеров;
2. Разбить данное сечение на простые фигуры, центры тяжести которых известны (С1, С2,...);
3. Провести рационально оси координат, так чтобы одна из осей проходила через ось симметрии, а вторая ось проходила через как можно больше центров тяжести простых фигур;
4. Записать формулы для расчетов:
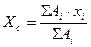 ;
; 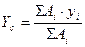 ;
;
 ;
;
Xc = 0, т.к. y – ось симметрии;
А1 =  = 8 м2; А1 = А2 = 8м2;
= 8 м2; А1 = А2 = 8м2;
А3 = 10 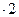 = 20 м2;
= 20 м2;
А4 = 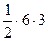 = 9 м2;
= 9 м2;
y3 =  = 3 м; y1 = y2 = 0; y4 =
= 3 м; y1 = y2 = 0; y4 =  м;
м;
yc =  = 2,333 м.
= 2,333 м.
5. Указать положение центра тяжести на схеме (т. С и координаты Хс:Yc);
6. Записать ответ.
Ответ. Точка С (0;2;3).
Задание для расчетно-графической работы № 3 (задача 1). Определить координаты центра тяжести сечения по данным одного из вариантов, показанных на рис.12. Показать положение центра тяжести на сечении.




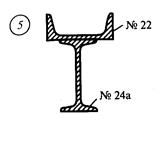
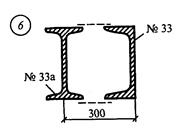



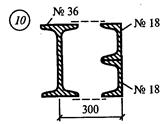





















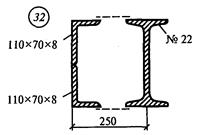
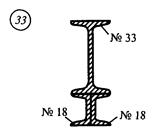
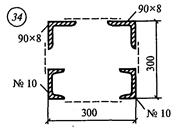

рис. 12
Задание для расчетно-графической работы № 3 (задача 2). Определить положение центра тяжести составного сечения из простых геометрических фигур

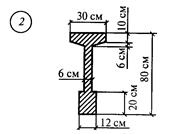





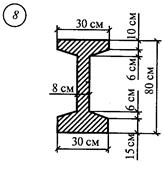





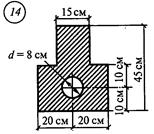


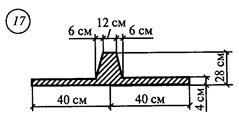





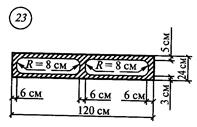









рис.13
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 4
Тема: «Растяжение и сжатие»
Цель работы:
Построение эпюр продольных сил, нормальных напряжений для ступенчатого бруса, защемленного одним концом, при осевом растяжении (сжатии). Определение абсолютного продольного удлинения (укорочения) бруса.
Студент должен знать:
- закон Гука;
- продольные и поперечные деформации при растяжении (сжатии);
- метод сечений.
Студент должен уметь:
- строить эпюры продольных сил и нормальных напряжений;
- определять усилия в сечениях;
- определять нормальные напряжения в сечениях.
Вопросы для самоконтроля:
- Что называется абсолютным продольным удлинением бруса?
- Что называется относительным продольным удлинением бруса?
- Какова размерность относительного удлинения бруса?
- Каковы единицы измерения модуля продольной упругости?
- Что называется жесткостью стержня при растяжении (сжатии)?
- Физический смысл коэффициента Пуассона.
- Формула экспериментального выражения закона Гука.
- Формула для определения нормального напряжения в сечении.
- В чем состоит отличие прямого бруса от ступенчатого?
- В чем состоит суть метода сечений?
- Что называется характерными точками?
- Что называется характерными участками?
- Что называется основной линией?
Методические указания
Когда к стержню приложены по концам две равные противоположно направленные силы, действующие по его оси, в стержне возникает деформация растяжения или сжатия.
Для определения внутренней продольной силы и нормального напряжения необходимо воспользоваться методом сечений

рис. 14
1) сечение 1-1 проводится перпендикулярно оси стержня;
2) сечение сквозное;
3) рассматривается равновесие любой отсеченной части:  , т.е.
, т.е.
N =  .
.
В случае растяжения продольная сила N считается положительной, при сжатии – отрицательной. Изменение продольной силы по длине стержня удобно представить в виде графика, называемого эпюрой продольных сил.
Напряжение, возникающее внутри бруса, действует перпендикулярно (нормально) сечению, поэтому называется нормальным напряжением
 ,
,
где N – продольная сила,
А – площадь поперечного сечения стержня.
Изменение нормального напряжения по длине бруса представим также в виде эпюры нормальных напряжений.
При деформации растяжение (сжатие) стержень либо удлиняется, либо укорачивается. Удлинение (укорочение) стержня определяется по формуле
 ,
,
где N – продольная сила,
l – длина рассматриваемого участка,
Е – модуль продольной упругости,
А – площадь поперечного сечения.
Пример. Для ступенчатого бруса построить эпюры продольных сил и нормальных напряжений. Определить абсолютное продольное удлинение или укорочение бруса.
Дано:
F1 = 28 кН
F2 = 64 кН
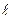 1 = 2,4 м
1 = 2,4 м
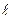 2 = 2,2 м
2 = 2,2 м
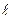 3 = 2,0 м
3 = 2,0 м
А1 = 3,2 см2
А2 = 6,4 см2
Е = 2,1  МПа
МПа

рис. 15
1.Обозначить характерные точки (A, B, C, D).
2.Обозначить характерные участки, начиная со свободного конца бруса (I, II, III).
3.Провести сквозные сечения на каждом характерном участке (1-1, 2-2, 3-3).
4.Определить продольную силу в каждом сечении
N1 = F1 = 28 кН
N2 = F1 = 28 кН
N3 = F1 – F2 = 28 – 64 = - 36 кН.
5.По найденным значениям продольной силы построить соответствующую эпюру (эпюра N). Для этого параллельно оси бруса проведем основную линию. Левее её откладываем значения N, соответствующие сжатому участку, а правее – положительные значения N, соответствующие растянутому участку.
6.Определить напряжения в каждом сечении
 = 87,5 Мпа;
= 87,5 Мпа;
 ;
;
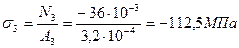 .
.
7.По найденным значениям нормальных напряжений построить соответствующую эпюру (эпюру 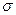 ).
).
8.Определить абсолютное удлинение бруса (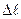 ).
).




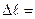 1 + 0,45 – 1,06 = 0,39 мм
1 + 0,45 – 1,06 = 0,39 мм
Таким образом, абсолютное удлинение бруса
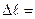 0,39 мм.
0,39 мм.
Задание для расчетно-графической работы № 4. Для ступенчатого бруса построить эпюры продольных сил и нормальных напряжений. Определить абсолютное продольное удлинение или укорочение бруса. Данные для своего варианта выбрать из табл. 3 и рис.16.







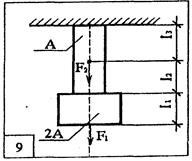

рис. 16
Таблица 3
| Вариант | Схема | F1, кН | F2, кН | А, см2 | 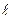 1, м 1, м
| 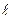 2, м 2, м
| 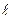 3, м 3, м
|
| 1,0 | 1,8 | 1,6 | |||||
| 1,2 | 2,0 | 1,0 | |||||
| 3,5 | 1,4 | 1,8 | 1,2 | ||||
| 4,5 | 1,6 | 1,6 | 2,4 | ||||
| 4,0 | 1,8 | 1,4 | 1,2 | ||||
| 6,5 | 2,0 | 1,2 | 1,4 | ||||
| 7,5 | 1,8 | 1,2 | 2,0 | ||||
| 7,0 | 1,6 | 1,4 | 1,8 | ||||
| 6,0 | 1,4 | 1,6 | 1,6 | ||||
| 5,0 | 1,2 | 1,8 | 1,4 | ||||
| 4,0 | 1,2 | 1,6 | 1,4 | ||||
| 7,5 | 1,4 | 1,4 | 1,2 | ||||
| 6,0 | 1,6 | 2,0 | 1,4 | ||||
| 5,0 | 1,8 | 1,4 | 2,0 | ||||
| 1,6 | 2,0 | 1,6 | |||||
| 1,4 | 1,8 | 1,6 | |||||
| 3,5 | 2,0 | 1,4 | 1,8 | ||||
| 4,5 | 1,4 | 1,8 | 1,6 | ||||
| 4,0 | 1,2 | 2,0 | 1,4 | ||||
| 6,5 | 1,4 | 1,6 | 1,2 | ||||
| 7,5 | 1,6 | 1,4 | 1,8 | ||||
| 1,4 | 1,2 | 2,0 | |||||
| 1,6 | 1,2 | 2,2 | |||||
| 1,8 | 1,6 | 2,1 | |||||
| 2,0 | 1,8 | 1,9 | |||||
| 1,4 | 1,9 | 2,1 | |||||
| 4,5 | 1,2 | 2,1 | 1,4 | ||||
| 7,5 | 2,4 | 1,4 | 1,2 | ||||
| 1,2 | 1,6 | 1,8 | |||||
| 1,0 | 2,0 | 2,1 | |||||
| 1,6 | 1,8 | 2,0 | |||||
| 3,5 | 2,0 | 1,6 | 1,4 | ||||
| 1,9 | 1,4 | 2,0 | |||||
| 1,7 | 1,2 | 1,9 |






