РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 11

Тема: «Трехшарнирные арки»

Цель работы:

1. Определение опорных реакций.
2. Определение поперечной силы, изгибающего момента и продольной силы в произвольном сечении арки.
3. Построение эпюр поперечных сил, изгибающих моментов и продольных сил.

Студент должен знать:

1. внутренние силовые факторы;
2. аналитический расчет трехшарнирной арки.

Студент должен уметь:

1. определять внутренние силовые факторы в произвольном сечении арки.

Вопросы для самоконтроля:

1. В чем отличие распорной системы от безраспорной?
2. Каково назначение затяжки (в случае устройства арки с затяжкой)?
3. Как определяют усилие в затяжке?
4. По каким правилам определяют поперечные силы, изгибающие моменты и продольные силы в сечениях арки?
5. Почему для построения эпюр Q,M, N при действии на арку сосредоточенных сил недостаточно определить значения этих внутренних усилий в начале и конце каждого участка, чего достаточно для построения эпюр для балок с прямой осью?
6. Каков порядок и принцип построения многоугольника и кривой давлений?
7. Что такое рациональное очертание оси арки?
8. Что называется сводом?

9. В чем сходство расчета арки и свода?

Методические указания

Арка (свод) есть криволинейный брус (плита), жесткое или шарнирно опертый пятами на опору.

С очки зрения статистики, принципиального различия между аркой и сводами нет, так как и арка и свод – системы распорные.

Распорной называется система, у которой вертикальная нагрузка вызывает опорные реакции. Горизонтальная составляющая наклонной называется распором. Она обозначается буквой Н.

Опоры арки называются пятами, а наиболее высокая точка ее оси – ключом или замком.

а

б

в

 

рис. 32

 

Трехшарнирной называется арка, состоящая из двух криволинейных стержней, соединенных между собой шарниром и имеющая две шарнирно-неподвижные опоры (рис.31а).

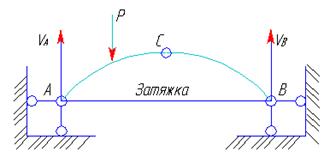
Наличия распора требует устройства массивных опор. Если по каким- либо причинам устройство таких опор невозможно, то опорные шарниры арки связывают между собой стержнем – затяжкой, воспринимающей распор арки. Затяжка может быть расположена и несколько выше опорных шарниров. Одна из опор трехшарнирной арки с затяжкой делается шарнирно - подвижной, так как ее геометрическая неизменяемость в этом случае обеспечивается наличием затяжки.

При действии на арку внешней нагрузки в ее сечениях в общем случае возникают поперечные силы, изгибающие моменты и продольные силы (в частных случаях отдельные силовые факторы могут отсутствовать).

Определение опорных реакций в трехшарнирной арки и внутренних усилий в ее сечениях может быть выполнено аналитическим или графическим способом.

Трехшарнирная арка статически определима, так как для нахождения четырех неизвестных составляющих опорных реакций можно написать три уравнения равновесия для арки в целом в одно дополнительное уравнение, выражающее равенство нулю изгибающего момента в промежуточном шарнире С.

Из уравнения ∑М_А = 0 находят опорную реакцию V_B, из уравнения ∑М_В = 0 или ∑Y = 0 - реакцию V_А. Правильность определения вертикальных реакций в первом случае проверяют соблюдением условий равновесия ∑Y = 0, во втором – условия ∑М_В = 0. Далее из уравнения 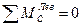определяют горизонтальную реакцию H_A, а из уравнения или из уравнения ∑Х = 0 - горизонтальную реакцию H_В. В первом случае контролем правильности определения реакций Н_А и Н_В будет соблюдение условий равновесия ∑Х = 0, во втором – условия .

Следует иметь ввиду, что при вертикальных нагрузках распор Н_А = Н_В = Н. Поэтому для определения распора Н в этом случае можно составить уравнение 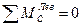, для проверки уравнение или наоборот. Приведенный порядок определения опорных реакций применим для трехшарнирных арок с опорами на одном уровне.

Если опоры трехшарнирной арки расположены в разных уровнях (рис. 31в), то опорные реакции могут быть определены в такой последовательности. Составляют и решают совместно уравнения и , в результате чего находят реакции V_B и H_B. Затем из уравнения ∑Y = 0 находят реакцию V_A, а из уравнения ∑Х = 0 – реакцию Н_А. Для проверки правильности вычисленных реакций составляют уравнение 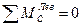или уравнение моментов всех сил, приложенных к арке, относительно какой-либо другой точки, выбранной с таким расчетом, чтобы моменты реакций V_А и H_А относительно нее не были равны нулю.

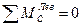Можно избежать совместного решения двух уравнений с двумя неизвестными, если полные реакции А и В разложить на вертикальные V_A’ и V_B’ и наклонные составляющие H_A’ и H_B’, направленные по прямой, проходящей через центры опорных шарниров. Тогда составляющие V_A’ и V_B’ определяются из уравнений и , а составляющие Н_A’ и Н_B’– из уравнений и .

В этом случае вертикальные V_А и V_В и горизонтальные Н_А и Н_В составляющие опорных реакций будут равны:

V_А = V_А + Н_А∙sinα; V_В =V_В – Н_В∙sinα; Н_А = Н_А∙cosα; Н_В = Н_В∙cosα.

После нахождения опорных реакций в зависимости от поставленных в задаче условий определяют поперечные силы, изгибающие моменты и продольные силы в отдельных заданных сечениях или строят эпюры Q, M и N для арки в целом.

При определении поперечной силы в сечении арки необходимо все силы, действующие по одну сторону от него, спроецировать на ось, перпендикулярную к касательной, проведенной к оси арки в данном сечении. При этом все вертикальные силы надо умножить на косинус, а горизонтальные – на синус угла наклона касательной к горизонту. Если составляющая сила, параллельная рассматриваемому сечению, стремится сдвинуть левую часть арки вверх или правую вниз, то вызванную ею поперечную силу считать положительной, если же наоборот, то отрицательной.

Для определения изгибающего момента в любом сечении берут сумму моментов всех сил слева или справа относительно центра сечения.

Определяя продольную силу в сечении арки, все силы, расположенные по одну сторону от него, необходимо спроецировать на касательную к оси арки в данном сечении (все вертикальные силы умножают на синус, а горизонтальные – на косинус угла наклона касательной к горизонту). Продольную силу будем считать положительной, если рассматриваемая внешняя сила вызывает в сечении арки сжатие, и отрицательной, если она вызывает растяжение.

 

рис. 33

 

Пример. Для трехшарнирной арки построить эпюры внутренних силовых факторов (рис. 32).

Решение (в общем виде)

Определение опорных реакций трехшарнирной арки производится точно таким же образом, как и для простой балки.

ΣМ_А = - V_В∙l – P₃ ∙ а₃ + Р₂ ∙ а₂ – Р₁ ∙ а₁ = 0;

;

ΣМ_В = V_А∙l – Р₁(l - а₁) - Р₂(l – а₂) – P₃(l - а₃) = 0;

.

Из предыдущего вычисления видно, что величина вертикальных составляющих опорных реакций от крутизны арки не зависит.

ΣХ = Н_А – Н_В = 0; Н_А = Н_В.

Горизонтальные составляющие опорных реакций (распор) равны между собой по величине и направлены в разные стороны.

Для определения их величины, возьмем МС (где изгибающий момент = 0),

Σ М_С = V_А∙l – P₁(l₁ - а₁) – Р₂(l₁ – а₂) – Н_А∙f = 0;

Таким образом, величина распора обратно пропорциональна величине стрелы подъема. Числитель в определении “Н_А” равен моменту относительно сечения “С” для простой балки “М_С”.

Равнодействующая Н_А и V_А 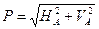; а угол наклона

рис. 34

Определение изгибающего момента, поперечной и продольной сил в любом сечении арки (рис. 33).

Изгибающий момент в сечении “К” арки будет:

М_К = V_АХ - Р₁(х – а₁) – Н_А ∙ У = 0, но V_АХ – Р1(х – а1) есть (изгибающий момент в сечении “К” простой балки).

Таким образом, изгибающий момент в любом сечении арки равен изгибающему моменту такого же сечения простой балки, уменьшенному на величину момента от распора Н_А ∙ У.

М_К = - Н_А ∙ У.

Поперечная сила в сечении “К” арки будет:

QК = V_А ∙ cosφ - P₁∙cosφ - H_А∙sinφ.

По аналогии с предыдущим

Q_К = – H ∙ sinφ

Продольная сила в сечении “К” арки будет:

N_К = V_А∙sinφ – P1∙sinφ + HА∙cosφ

выражение VА∙sinφ – P1∙sinφ есть поперечная сила в сечении “К” простой балки и тогда

N_К = ∙sinφ + H ∙ cosφ

При построении эпюр М, Q, N для четырехшарнирной арки необходимо обратить внимание на их формулы. И тогда станет понятным, что для построения эпюры изгибающих моментов арки следует построить эпюру изгибающих моментов для балки равного пролета от нагрузок, действующих на арку, и вычесть из ординат этой эпюры, соответствующие моментам от распора.

А для построения эпюры поперечных сил арки необходимо из ординат балочной эпюры Q⁰, умноженной на cosφ, вычесть ординаты поперечной силы от распора Н∙sinφ.

Эпюра N строится путем суммирования ординат “балочной” эпюры Q⁰, умноженной на sinφ в этом сечении, и ординаты нормальной силы от распора (Н∙cosφ).

Арка (свод) отличаются от балки тем, что в результате искривления оси в ней возникают сжимающие усилия от действия распора, тем самым уменьшаются значения М и Q.

Очевидно, что рациональным искривлением оси арки будет такое, при котором суммарный изгибающий момент на всем протяжении арки будет равен нулю.

Требование, чтобы изгибающие моменты во всех сечениях трехшарнирной арки были равны нулю, приводит к равенству:

М_Х = – Н_Х ∙ У = 0, откуда У =

Коэффициентом пропорциональности в этом соотношении, связывающем ординаты рациональной оси арки с ординатами эпюры М простой балки, является величина распора Н, зависящая от расположения шарниров (пологий или подъемный свод).

В практике встречаются различные по форме и виду арки. Для некоторых очертаний арок приведем уравнения их изогнутых осей.

1. при очертании арки по параболе уравнение оси:

;

2. при очертании арки по эллипсу уравнение оси:

;

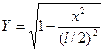3. при очертании по части окружности уравнение оси:

,

где: К = R – 1.

В частном случае при R = f очертание арки принимает вид полуокружности и уравнение оси упрощается:

В обоих случаях

При любом очертании арки рекомендуется следующий порядок расчета.

1. Определяются вертикальные реакции V_А и V_В по уравнениям: ΣM_B = 0 и ΣM_A =0. Затем проверяется правильность определения реакций по уравнению проекций ΣY_i= 0.

Усилие в затяжке Н = Н_А = - Н_В определяется из уравнения моментов внешних сил относительно шарнира С для одной из половин арки. Например, из рассмотрения равновесия левой части арки Н =

2. По заданному очертанию определяются геометрические характеристики оси арки, т.е. для выбранных точек 1, 2, … i находим х_i, у_i, а также углы наклона касательной в этих точках к направлению х затяжки.

3.В сечениях, проведенных через выбранные точки, определяются внутренние силовые факторы по формулам:

М = - Н_уi; Q_i = ∙ cosα_i – H ∙ sinα_i; N_i = - ( ∙ sinα_i + H ∙ cosα_i),

Где M_i, Q_i, N_i – изгибающий момент, поперечная сила и нормальная сила в поперечном сечении арки; , - изгибающий момент и поперечная сила в простой балочной системе; Н – усилие в затяжке; α - угол, образуемый касательной в точке i и горизонталью, который определяется из значений первой производной оси арки .

Задание для расчетно-графической работы № 11. Определить изгибающие моменты, поперечные силы и продольные силы в пяти точках трехшарнирной арки: опорах, промежуточном шарнире и серединах левой и правой полуарки по данным одного из вариантов.

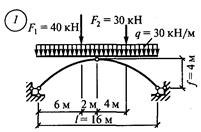
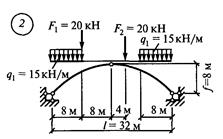
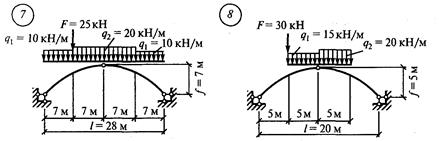
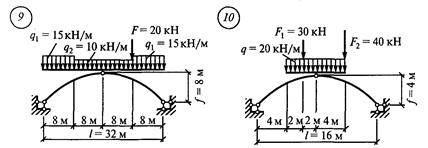
рис. 35
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 12

Тема: «Плоские статически определимые фермы»

Цель работы: Графическим способом определить усилия в стержнях фермы.

Студент должен знать:

1. условия геометрической неизменяемости и статической определимости;
2. методику расчета фермы графическим и аналитическим способами.

Студент должен уметь:

1. определять усилия в стержнях фермы аналитическим и графическим методом (путем построения диаграммы Максвелла - Кремоны).

Вопросы для самоконтроля:

1. Дайте определение понятию «ферма»

2. Перечислите основные элементы фермы.

3. Что такое узел фермы?

4. Как определяется узловая нагрузка?

5. Что такое решётка фермы?

6. Что понимается под внешними полями фермы? Как они обозначаются?

7. Что понимается под внутренними полями фермы? Как они обозначаются?

8. Как строится силовой многоугольник внешних сил? Порядок построения.

9. Перечислите последовательность построения диаграммы внутренних усилий в стержнях фермы.

10. Как определяется по диаграмме величина и направление усилий в стержнях фермы?

 

Методические указания

Внешние поля фермы - область, ограниченная с двух сторон двумя соседними внешними силами (), с третьей стороны поясом фермы. Внешние поля разомкнуты с одной стороны, обозначаютсяa, b, c, d... - строчными буквами латинского алфавита при обходе фермы по часовой стрелке. (в данной работе начиная обход от опоры А). Если ферма и нагрузки имеют ось симметрии, то симметричные поля правой половины можно обозначить теми же буквами, но с индексами a¹, b¹, c¹, d¹…

Внутренние поля - замкнутая область внутри решетки фермы, ограниченная стержнями, обозначается цифрами 1, 2, 3, 4,… при обходе фермы слева - направо. Симметричные поля правой половины можно обозначить теми же цифрами, но с индексами 1’, 2’, 3’, 4’…

Узел фермы - место соединения нескольких стержней;

Узловая нагрузка- нагрузка, приходящаяся на узел фермы.

Верхний пояс фермы – соединение стержней верхнего контура фермы.

Нижний пояс фермы – соединение стержней нижнего контура фермы.

Графический способ расчета основан на построении многоугольника сил.

Пример. Для заданной статически определимой фермы определить опорные реакции фермы, построить диаграмму Максвелла - Кремоны, определить числовые значения усилий, составить таблицу расчетных усилий. Данные для расчета взять из таблиц.

 

Решение

1. Вычертить геометрическую схему фермы, обозначив все узлы буквами A, B, C, D, E в масштабе 1:n (n = 100, 200, 250, 400) с указанием в узлах заданной нагрузки и направления опорных реакций V_A, V_B;

 

2. Определить опорные реакции фермы V_A, V_B

V_A = V_B = ₌ 2 20 = 40 кН;

Узловая нагрузка , приходящаяся на крайние узлы фермы определяется по формуле:

F/2 = = 5 ∙ 4/2 = 10 кН;

где q - интенсивность равномерно-распределенной нагрузки; q = 5 ;

l - длина панели фермы (расстояние между соседними узлами фермы) l =4м;

3. Обозначить внешние поля фермы a, b, c, d, е, f, k;

4. Обозначить внутренние поля фермы 1, 2, 3, 4, 5, 6, 7, 8;

5. Построить диаграмму;

5.1 Выбор масштаба сил: в 1 мм - 1 кН;

5.2 Построить многоугольник внешних сил. Так как эта система параллельных сил уравновешена, то замкнутый силовой многоугольник превращается в две накладывающиеся друг на друга вертикальные линии:

Строим силовую линию а - b - с - d - e - f внешних сил, которые встречаются по обходу часовой стрелки, для этого откладываем вертикально вниз, от точки «а», в принятом масштабе отрезок (a - b), равный 10 мм и соответствующий силе , затем от точки «b», до точки «с» откладываем отрезок (b - c) равный 20 мм и соответствующий силе F, и так далее до точки f.

От точки f строим силовую линию реакций связи (направленную вертикально вверх).

Силу V_B (f - k) направленную вертикально вверх откладываем от точки «f» до точки «k» (в принятом масштабе она соответствует отрезку 40 мм), соответственно силу V_А (k – а) - от точки «k» до точки «а». В результате получаем замкнутый силовой многоугольник.

6. Построение диаграммы усилий.

Узел С.

Мысленно вырезаем узел С, в котором сходятся два стержня, (b - 1, 1 - a) На силовой линии есть точки «а» и «b». Через точку «b» проводим линию параллельную стержню b - 1, через точку «а» проводим линию параллельную стержню 1 - а, точка их пересечения обозначается цифрой 1. В нашем случае она совпадает с точкой «b».

Знаки и величину усилий определяют следующим образом. Силовой многоугольник, построенный для данного узла С, должен быть замкнут, направление сил - по часовой стрелке. От точки «b» к точке «1», далее от точки «1» направлено к точке «а», от точки «а» к точке «b». Мысленно переносим эти направления на соответствующие стержни фермы, видим, что на диаграмме точка «b» совпадает с точкой «1», следовательно усилие b - 1 равно нулю, усилие 1 - а направлено от точки «1» к точке «а» («снизу вверх» на диаграмме – «к узлу» на схеме фермы -следовательно стержень сжат). Величина усилия определяется как произведение масштаба на расстояние между точками, соответствующими стержням.

S_b-1=0; S_1-a=10 = кН.

Узел А.

В нем сходятся три стержня (a-1, 1-2, 2-к), на диаграмме уже есть точки «а», «1», «к». Усилие в стержне a - 1 определено, для определения усилий в стержнях (1-2, 2-к) проводим через точку 1 прямую, параллельную стержню 1-2, а через точку «к» прямую параллельную стержню 2-к, до взаимного пересечения в точке 2. Аналогично вырезаем узлы D, P, E, N, F, L, V.

Узел D.

В нем сходятся четыре стержня (c-3, 3-2, 2-1, 1-b). Усилие в стержнях 2-1, 1-b определено, для определения усилий в стержнях (c-3, 3-2) проводим через точку «с» прямую, параллельную стержню c-3, а через точку «2» прямую параллельную стержню 3-2, до взаимного пересечения в точке «3».

 

Узел Р.

В нем сходятся четыре стержня (2-3, 3-4, 4-к, к-2). Усилие в стержнях 2-3, к-2 определено, для определения усилий в стержнях (3-4, 4-к) проводим через точку «3» прямую, параллельную стержню 3-4, а через точку «к» прямую параллельную стержню 4-к, до взаимного пересечения в точке «4».

 

Узел N.

В нем сходятся три стержня (4-5, 5-к, к-4). Усилие в стержне 4-к определено, для определения усилий в стержнях (4-5, 5-к) проводим через точку «4» прямую, параллельную стержню 4-5, а через точку «к» прямую параллельную стержню к-5, до взаимного пересечения в точке «5». Точка «4» совпадает с точкой «5».

 

Узел Е.

В нем сходятся пять стержней (d-6, 6-5, 5-4, 4-3, 3-c) Усилие в стержнях 5-4, 4-3, 3-с определено, для определения усилий в стержнях (d-6, 6-5) проводим через точку «d» прямую, параллельную стержню d-6, а через точку «5» прямую параллельную стержню 6-5, до взаимного пересечения в точке «6».

 

Узел M.

В нем сходятся четыре стержня (6-7, 7-k, k-5, 5-6) Усилие в стержнях k-5, 5-6 определено, для определения усилий в стержнях (6-7, 7-k) проводим через точку «6» прямую, параллельную стержню 6-7, а через точку «к» прямую параллельную стержню 7-к, до взаимного пересечения в точке «7».

 

Узел F.

В нем сходятся четыре стержня (e-8, 8-7, 7-6, 6-d) Усилие в стержнях 7-6, 6-d определено, для определения усилий в стержнях (e-8, 8-7) проводим через точку «e» прямую, параллельную стержню e-8, а через точку «7» прямую параллельную стержню 8-7, до взаимного пересечения в точке «8», совпадающей с точкой «e».

 

Узел L (проверочный).

Мысленно вырезаем узел L, в котором сходятся два стержня (f-8, 8-e) На силовой линии есть точка «8», совпадающая с «е» и точка «f.».

Измеряя расстояния сравниваем значения с полученными значениями сил.

 

Найденные усилия записываем в таблицу.

 

 

Таблица 6

Элементы фермы	Наименование стержней	Усилие, кН
«+» растяжение	«-» сжатие
Верхний пояс	b-1, e-8
	c-3, d-6
Нижний пояс	2-k, 7-k
	4-k, 5-k
Стойки	1-а, 8-f
	2-3, 6-7
Подвески	4-5
Раскосы	1-2, 7-8
	3-4, 5-6

Вывод: Стержни верхнего пояса CD, DE, EF, FG- сжаты, стержни нижнего пояса АР, РN, NM, VB растянуты.

рис. 36

 

 

Задание для расчетно-графической работы № 12. Для статически определимой фермы рассчитать усилия графически и аналитическим способами. Исходные данные взять из табл. 7 и рисунка 37.

 

Таблица 7

№ варианта	№ схемы	q, кН/м	d, м	h, м
	а
	b
	c
	d
	e
	f

 

Схема	№ схемы
	a
	b
	c
	d
	e
	f

 

рис. 37