Тема: «Изгиб прямого бруса»
Цель работы:
Построение эпюр поперечных сил и изгибающих моментов по длине балки
Студент должен знать:
- формулы для определения внутренних силовых факторов при изгибе;
- дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.
Студент должен уметь:
- строить эпюры поперечных сил и изгибающих моментов по длине балки, проверять правильность их построения.
Вопросы для самоконтроля:
1. Какой изгиб называется прямым, косым?
2. Какой изгиб называется чистым, поперечным?
3. Как вычисляется изгибающий момент и поперечная сила в сечении балки?
4. Сформулировать правила знаков для поперечной силы и изгибающего момента.
5. Изменяется ли значение поперечной силы в сечении, если в его плоскости балка нагружена сосредоточенным моментом?
6. Для чего строятся эпюры поперечных сил и изгибающих моментов?
7. Сформулировать правила построения эпюры поперечных сил.
8. Сформулировать правила построения эпюры изгибающих моментов.
9. Что называется основной линией?
10. Что называется характерными точками и характерными участками?
Методические указания
1. Определить опорные реакции балки (см. порядок решения задачи расчетно-графической работы № 2).
2. Обозначить характерные сечения (точки) балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки.
З. Построить эпюру поперечных сил Qу. Для этого определяют значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Qлев и Qправ.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qу.
4. Построить эпюру изгибающих моментов Мх. Для этого определяют изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее, Изгибающие моменты в этих точках обозначаются соответственно Млев и Мправ. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.
Парабола имеет выпуклость в сторону действия нагрузки (при действии нагрузки сверху парабола обращена выпуклостью вниз). При этом, если эпюра Qу на рассматриваемом участке не пересекает нулевую линию, то эпюра Мх (она является параболой) может быть построена по двум точкам, так как все значения изгибающих моментов в промежуточных точках находятся между значениями в характерных сечениях. Если эпюра Qу пересекает нулевую линию, то под этим сечением эпюра Мх будет иметь экстремальное (максимальное или минимальное) значение или вершину параболы. Положение этой точки находят по эпюре из подобия треугольников (см. примеры). Затем находят значение изгибающего момента в этом сечении и строят эпюру М на участке с распределенной нагрузкой по трем точкам.
Соединив все значения изгибающих моментов по указанным правилам, получают график изменения изгибающих моментов по длине балки. Такой график называется эпюрой Мх.
Приведенный способ построения эпюр Qу и Мх назовем способом построения эпюр по характерным сечениям. Такой способ является частным случаем более общего, хотя и более трудоемкого способа, который называется способом построения эпюр по участкам. Порядок построения эпюр при этом способе следующий:
- балку разбивают на участки;
- границами участков являются характерные сечения;
- для каждого участка записывается закон изменения усилий Qу и Мх и определяются их величины при граничных значениях;
- по найденным величинам усилий строят соответствующие эпюры.
Существует несколько способов проверки правильности построения эпюр. Наиболее простой способ проверки заключается в том, что суммы моментов всех левых и всех правых сил, взятые отдельно, в любой точке балки должны быть равны между собой.
Задача. Построить эпюры Qу и Мх для балки.
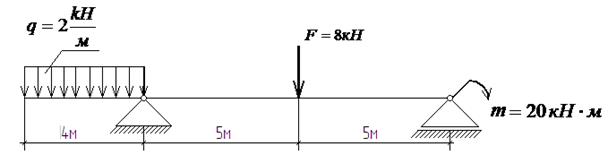
Решение
1. Определить опорные реакции балки.
Составить уравнения по условиям равновесия:
∑MA=0, ∑Fy=0,
∑MA=0, - Fq*2 + F*5 – RBY*10 + m = 0,
RBY = (-Fq*2+ F*5+ m)/10 = (-8*2+8*5+20)/10 = 4,4 kH
∑Fy=0, - Fq + RAY + RBY – F = 0,
RAY = Fq- RBY + F = 8+8-4,4 =11,6 kH
Выполнить проверку решения по условию:
∑MB=0, m- F*5 + RAY *10 - Fq*12 =0,
20 – 8*5+ 11,6*10 -8*12 = 20 -40+ 116 -96 = 0
2. Обозначить характерные сечения балки С, А, D, В.
3. Обозначить характерные участки I II III.
4.Построить эпюру поперечных сил Qу,
4.1. Определить значения поперечных сил в характерных точках по формуле:
Qy = ∑Fiy
QC = 0,
QAлев = - Fq = -8 kH,
QAправ = - Fq + RAY = -8 + 11,6 =3,6 kH
QDлев = - Fq + RAY = -8 + 11,6 =3,6 kH
QDправ = - Fq + RAY – F = - 8 + 11,6 – 8 = - 4,4 kH
QBправ = 0,
QBлев = – RBY = - 4,4 kH
По полученным значениям построить эпюру Qy, cоединяя полученные значения прямыми линиями.
4.2. Определить значения изгибающих моментов в характерных точках по формуле:
Mx =∑mi
Mc = 0,
MB = - m = -20 kH*м
MA = - Fq *2 = -8*2 = - 16 kH*м
MD = - m + RBY*5 = - 20 + 4,4 *5 = 2 kH*м
По полученным значениям построить эпюру Mx:
а) на участке CА действует распределенная нагрузка, поэтому эпюра Мх - парабола. Так как эпюра Qх на этом участке не пересекает нулевую линию, то парабола не имеет экстремального значения, поэтому величины изгибающих моментов в сечениях C и А соединим кривой, значения которой находятся в интервале 0 кН×м... - 16 кН×м;
б) на участках AD и DB нагрузки нет, поэтому эпюра Мх изображается прямыми линиями наклонными к нулевой (основной) линии.
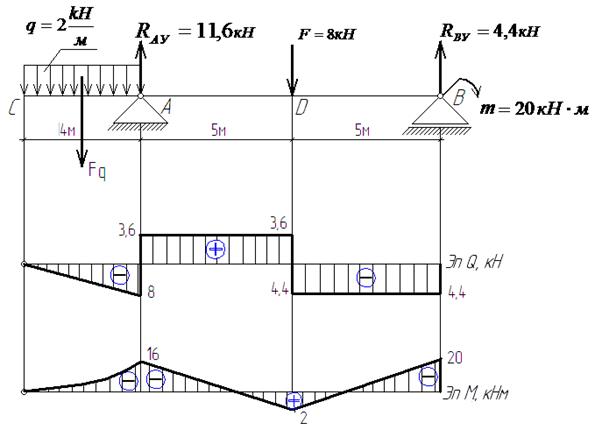
рис. 21
Задание для расчетно-графической работы № 7. Построить эпюры Qх и Мх по данным своего варианта. Исходные данные взять из расчетно-графической работы
№ 2 (задача 1) по теоретической механике.






