Тема: «Плоская система произвольно расположенных сил»
Цель работы:
Определение опорных реакций консольных и однопролетных балок
Студент должен знать:
- определение момента силы относительно точки, его свойства;
- условия равновесия плоской параллельной и произвольной системы сил;
- типы нагрузок и виды опор балок.
Студент должен уметь:
- определять опорные реакции балок.
Вопросы для самоконтроля:
- Что называется моментом силы относительно точки? Как выбирается знак момента?
- Что такое плечо силы?
- Изменится ли момент силы относительно данной точки при переносе силы по линии её действия?
- Сформулировать условия равновесия плоской системы произвольно расположенных сил.
- В каком случае момент силы относительно точки равен нулю?
- Как определить равнодействующую равномерно-распределенной нагрузки?
- Что значит привести силу к данному центру?
Методические указания (к примеру 1)
1. Заменить распределенную нагрузку её равнодействующей, которая является сосредоточенной силой.
Fq = q 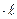
2. Обозначить опору.
В балке-консоли только одна опора-заделка, обозначим её буквой А.
3. Освободиться от опоры и заменить её действие на балку реакциями: вертикальной VА, горизонтальной НА и моментом МА.
4. Составить уравнения равновесия по условиям равновесия:
1) 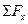 = 0, 2)
= 0, 2) 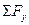 = 0, 3)
= 0, 3) 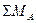 = 0.
= 0.
Решить уравнения и найти реакции VА, НА, МА.
5. Выполнить проверку решения. Для этого составляют уравнение равновесия по условию
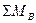 = 0.
= 0.
Если оно удовлетворено, то реакции найдены правильно, а если нет, то в решении допущена ошибка.
Пример 1. Определить опорные реакции балки-консоли.
Решение
1. Заменить распределенную нагрузку равнодействующей, Fq = q 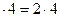 = 8 кН.
= 8 кН.
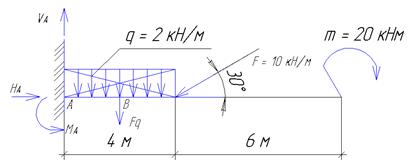
рис. 5
2. Обозначить опору А.
3. Указать предварительные направления опорных реакций VА, НА, МА.
4. Составить уравнения равновесия по условиям: 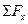 = 0,
= 0, 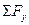 = 0,
= 0, 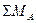 = 0.
= 0.
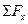 = 0,
= 0,  ,
,
 кН
кН
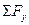 = 0,
= 0, 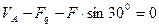 ,
,
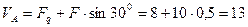 кН
кН
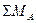 = 0,
= 0, 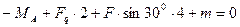 ,
,
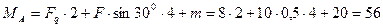 кН
кН 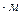 .
.
5. Выполнить проверку решения по условию:
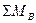 = 0, - МА + VF
= 0, - МА + VF 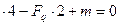
- 56 + 13 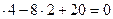 /
/
Реакции определены верно.
Ответ: НА = 8,66 кН,
VA = 13 кН,
МА = 56 кН 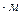 .
.
Методические указания (к примеру 2)
1. Заменить распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка 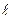 , на котором она действует:
, на котором она действует: 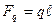 .
.
Перед решением задач рекомендуется уяснить и закрепить порядок нахождения равнодействующей и определения расстояний от нее до опор. При отсутствии навыков решения таких задач необходимо указывать положение равнодействующей относительно опор. В дальнейшем этого можно не делать.
2. Обозначить опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и вторую шарнирно-подвижную опору.
З. Освободиться от опор и заменить их действие на балку реакциями. На балку действуют только вертикальные нагрузки и сосредоточенные моменты. Реакции опор при такой нагрузке будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки) и обозначают реакцию опоры A – VA, а опоры В - VB.
4. Составить уравнения равновесия вида:
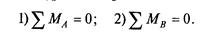
Напомним, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от этой точки приложения силы (в общем случае до линии действия силы).
Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать ее момент положительным, а если против – отрицательным. Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остается тем же, что для момента силы.
Решают уравнения и находят реакции VA и VB.
5.Выполнить проверку решения. Для этого составляют уравнение равновесия:
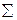 Fу = О.
Fу = О.
Если оно удовлетворено, то реакции найдены правильно, а если нет, то в решении допущена ошибка.
Пример 2. Определить опорные реакции двухконсольной балки.
Решение
1. Заменить распределенную нагрузку равнодействующей. На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдем равнодействующую:
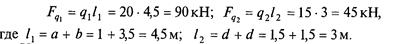
Укажем расстояния от этих сил до каждой из опор (рис. 6, 6).
2. Обозначить опоры А и В.
З. Указать опорные реакции VA и VB. Обычно рис. 6 а и б совмещают в одном.

а
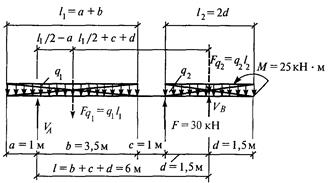
б
рис. 6
4. Составить уравнения равновесия. Первое уравнение для нашей задачи примет вид

откуда
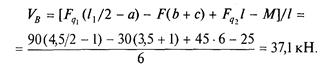
Второе уравнение примет вид
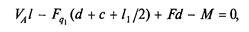
откуда
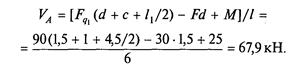
5. Выполнить проверку, используя уравнение 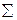 Fу = 0, которое примет вид
Fу = 0, которое примет вид
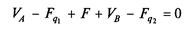
или
67,9—90+30+37,1—45=0, откуда 135—135=0.
Реакции определены правильно.
Ответ: VА= кН; VВ = 37,1 кН.
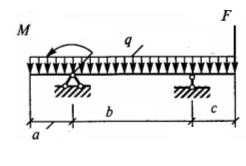
Задание для расчетно-графической работы № 2(задача 1). Определить опорные реакции балки–консоли. Исходные данные для своего варианта выбрать в таблице 1 и рисунке 7.
Таблица 1
| Вари-ант | Схема | a | b | F | 
| q | m | Вари-ант | Схема | a | b | F | 
| q | m |
| a | d | ||||||||||||||
| e | |||||||||||||||
| b | |||||||||||||||
| f | |||||||||||||||
| c | |||||||||||||||
| q | |||||||||||||||
| d | |||||||||||||||
a) 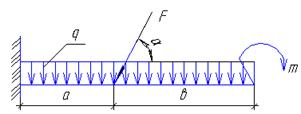 b)
b) 
c) 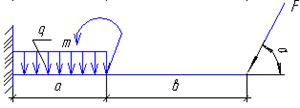 d)
d) 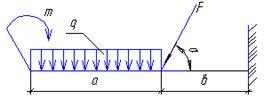
e) 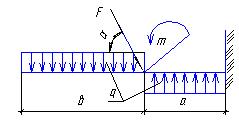 f)
f) 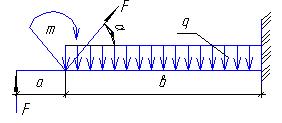
g) 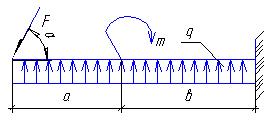
рис. 7
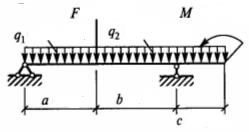
Задание для расчетно-графической работы № 2 (задача 2). Определить опорные реакции балки на двух опорах по данным одного из вариантов, показанных в таблице 2 и на рис. 8. Проверить правильность их определения.
Таблица 2
| Вари-ант | Схема | a | b | с | F | q | М | Вари-ант | Схема | a | b | с | F | q | М |
| м | м | м | кН | 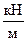
| Кн 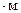
| м | м | м | кН | 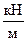
| Кн 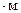
| ||||
| a | d | ||||||||||||||
| e | |||||||||||||||
| b | |||||||||||||||
| f | |||||||||||||||
| c | |||||||||||||||
| 1,5 | |||||||||||||||
| g | |||||||||||||||
| d | |||||||||||||||
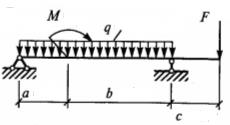
a b
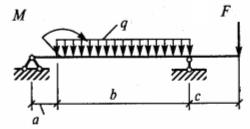
c d

e f
g
рис. 8






