Линейное уравнение с логарифмированием факторного признака

Для вычисления коэффициентов a и b для уравнения прямой с логарифмированием факторного признака

необходимо решить следующую систему уравнений:

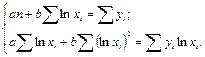
Решение системы относительно неизвестных a и b дает численные значения искомых коэффициентов:

Пример: Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя линейную модель с логарифмированием факторного признака.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 7.1.

 

 

Таблица 7.1 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi, см	Высота, yi,м	ln xi	(ln xi )2	yi ln xi	yx =-14,6 + 11,2 ln xi	yi – yx	(yi –yx)2	yi2
	9,5	2,0794	4,3241	19,75	8,723	0,7761	0,6023	90,25
	13,4	2,4849	6,1748	33,3	13,265	0,1341	0,018	179,56
	16,3	2,7726	7,6872	45,19	16,488	-0,1885	0,0355	265,69
и т.д.
	264,2	39,188	131,74		сумма	0,0594	3,9614	6293,9

 

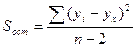
Полученное уравнение регрессии имеет вид y = -14,57 + 11,202 ln x. При уровне значимости α = 0,05 F_ф > F_st. Следовательно, линейное уравнение регрессии адекватно описывает фактическое изменение высот от диаметров деревьев.

Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что линейное уравнение с логарифмированием факторного признака, представленное результатами опыта у = -14,57 + 11,202 ln x в 109,5 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.

Представить графически изменение высот от диаметров для оценки адекватности модели по полученному уравнению. Построение графиков по исходным данным пунктирной линией (x_i,y_i), по расчетным данным сплошной линией (x_i, y_x).

 

Уравнение гиперболы

Для вычисления коэффициентов a и b гиперболической зависимости:

необходимо решить следующую систему уравнений:

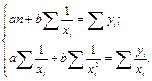
Результатом решения системы нормальных уравнений являются следующие выражения:

Проверка значимости уравнения регрессии производится по F - критерию Фишера. При этом общая дисперсия S_y² сравнивается с остаточной S_z²:

F_ф = S_y² / S_z

Для принятого уровня значимости F_ф сравнивается с табличным значением F_st и делается вывод об адекватности описания уравнением рассматриваемой взаимосвязи.

Пример: Получить уравнение регрессии, описывающее фактическое изменение высот от диаметров в сосновом древостое, используя линейную модель.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 1.8.2.

 

Таблица 7.2 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi, см	Высота, yi, м	1/xi	(1/xi)2	yi/xi	yi2	yx=30,965-197/xi	yi-yx	(yi-yx)2
	9,5	0,125	0,0156	1,1875	90,25	6,34	3,160	9,985
	13,4	0,083	0,0069	1,1167	179,56	14,543	-1,148	1,318
	16,3	0,063	0,0039	1,0188	265,69	18,6525	-2,353	5,534
и т.д.
	264,2	0,545	0,0357	9,8473	6293,90	сумма	-0,008	53,052

 

 

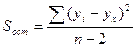
Полученное уравнение регрессии имеет вид y = 30,965 – 197 / x. При уровне значимости α = 0,05 F_ф > F_st. Следовательно, гиперболическое уравнение регрессии адекватно описывает фактическое изменение высот от диаметров деревьев.

Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что уравнение гиперболы, представленное результатами опыта у = 30,965 – 197 / х в 8,1761 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.

Представить графически изменение высот от диаметров (смотри уравнение гиперболы).