Таблица 1.6 Группировка данных, расчет вспомогательных величин для вычисления средней величины и суммы квадратов
отклонений
| Границы классов, см | Часто-та, ni, шт | Группо-вая вариан-та, xi, см | По исходным данным | По преобразованным данным | |||||
| ni × xi | xi2 | ni × xi2 | ai | ni × ai | ai2 | ni × ai2 | |||
| 6,0 – 10,0 | - 4 | - 8 | |||||||
| 10,1 – 14,0 | - 3 | - 12 | |||||||
| 14,1 – 18,0 | - 2 | - 22 | |||||||
| 18,1 – 22,0 | - 1 | - 16 | |||||||
| 22,1 – 26,0 | |||||||||
| 26,1 – 30,0 | |||||||||
| 30,1 – 34,0 | |||||||||
| 34,1 – 38,0 | |||||||||
| 38,1 – 42,0 | |||||||||
| 42,1 – 46,0 | |||||||||
| ∑ ni = n=100 | ∑ ni × xi = | ∑ ni × xi2= | ∑ ni × ai = | ∑ ni × ai2 = |
А – групповая варианта, которой соответствует наибольшее значение частоты. По выше приведённой таблице А = 24 см, т.к. частота данного класса будет максимальной.
После расчёта вспомогательных величин в таблице 1.6 приступают к вычислению основных статистических показателей для большой выборочной совокупности. Среднюю величину и сумму квадратов отклонений рассчитать по исходным и преобразованным данным. Численные значения названных статистических показателей по исходным и преобразованным данным должны быть равными.
По исходным данным
Средняя величина
,
где xi – групповая варианта.
Например: x = 2488 / 100 = 24,88 см.
Сумма квадратов отклонений
.
Например: СКО = 67456 – ((2488)2 / 100)2= 5554,56 см.2
По преобразованным данным
Средняя величина
.
Например: x = 24 + ((22/100)× 4)= 24,88 см.
x1 = x2 = 24,88 см.
,
где xi - групповая варианта; С - классовый интервал
Сумма квадратов отклонений
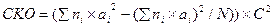
Например: СКО = (352 – (22 / 100)) × 16 = 5554,56 см.2
СКО1 = СКО2 = 5554,56 см.2
Далее производится расчёт остальных статистических показателей, их ошибок репрезентативности, и оценка достоверности.
Дисперсия:
.
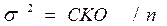Стандартное отклонение (среднее квадратичное отклонение):
.
Коэффициент вариации:
%.
По величине расчётного коэффициента вариации определяется уровень изменчивости признака с помощью шкалы Мамаева представленной в таблице 1.2.
Коэффициент дифференциации:
,
где где x0 – значение первого класса ряда распределения (нижняя граница первого класса ряда распределения)
Например по данным таблицы 1.6 нижняя граница первого класса ряда распределения будет равна 6,0 см.
Степень дифференциации признака определяется по величине коэффициента дифференциации с помощью таблицы 1.3.
Ошибки репрезентативности (представительности)
Ошибка средней величины:
.
Ошибка стандартного отклонения:
.
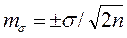Ошибка коэффициента вариации:
.
Ошибка точности:
.
Точность определения средней величины
(относительная ошибка опыта)
или 
.
Достоверность статистических показателей (надежность)
Достоверность средней величины: 
.
Достоверность стандартного отклонения: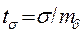 
.
Достоверность коэффициента вариации: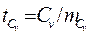 
.
Достоверность точности: 
.
