Если при обработке информации возникает задача установления связи между двумя величинами, то работу проводят в определенной последовательности:
- на график наносят значения пар (xi, yi) для визуальной оценки наличия и тесноты связи;
- если связь явно нелинейная, то вычисляют и оценивают корреляционное отношение η;
- если определенного заключения по графику сделать нельзя, то наряду с корреляционным отношением η вычисляют коэффициент корреляции r, после чего вычисляется мера линейности ε и ее основная ошибка mε:
.
.
Величина меры линейности характеризует отклонение связи от прямолинейной. Если ε / mε > 2, то гипотезу о нелинейности связи принимают, в противном случае (ε / mε < 2) связь приближенно можно считать линейной.
Для более точной оценки наличия криволинейности взаимосвязи пользуются F - критерием линейности корреляции, который сравнивается с табличным при уровнях значимости α = 0, 05 и α = 0,01 при К1 = Кх – 2 и К2 = n – 2 степенях свободы.
Fф =((η2 – r2) × (n – Кx)) 
/ ((1 – η2) × (Кx – 2)),
где η2 – квадрат корреляционного отношения y по x; r2 – квадрат линейной корреляции; n – объем выборки; Кx – число групп по ряду х.
Гипотеза о прямолинейности взаимосвязи отвергается, если Fр > Fт при уровне значимости α = 0,01 и принимается, если Fр < Fт при α = 0,05.
В природных, биологических объектах во всем диапазоне закономерных изменений зависимой переменной от независимой, как правило, проявляется криволинейность.
6.1. Расчёт показателей корреляции на примере малой выборочной совокупности
Расчет вспомогательных величин для вычисления коэффициента корреляции приведен в таблице 6.1.
Таблица 6.1 Расчет вспомогательных величин для коэффициента корреляции
| Значение признака | xi2 | yi2 | xi × yi | |
| Диаметр, хi, см | Высота, yi, м | |||
| 16,2 | 17,5 | 262,44 | 306,25 | 283,50 |
| 29,7 | 21,3 | 882,09 | 453,69 | 632,61 |
| 20,8 | 22,7 | 432,64 | 515,29 | 472,16 |
| И т.д | … | … | … | … |
| ∑ xi 613,4 | ∑ yi 583,8 | ∑ xi2 14047,96 | ∑ yi2 12003,78 | ∑ xi × yi 12769,18 |
Вычисление вспомогательных величин:
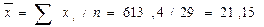см
м
где n – это объём выборочной совокупности (по примеру n = 29)
;
;
,
Формула расчета коэффициента корреляции:
.
Например: 
.
Ошибка коэффициента корреляции:
.
Например: 
.
Значимость корреляции:
.
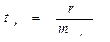Например: 
.
Число степеней свободы:
.
Например: 
.
t – критерий Стьюдента на 5 % уровне значимости (определяется по таблице учебника) исходя из числа степеней свободы
t 05 = 2,045
t r= 7,36 > t05, значит корреляция значима.
Расчет вспомогательных величин для вычисления корреляционного отношения приведен в таблице 6.2.
Для расчёта вспомогательных величин необходимо произвести группировку данных по независимой переменной или разбить все данные на классы с равной величиной классового интервала.
В курсовой работе данные группируются в ступени толщины с величиной классового интервала 4 см. ступени толщины не пропускаются, при этом число деревьев в ступени должно быть не менее двух.
Таблица 6.2 Расчет вспомогательных величин для вычисления корреляционного отношения
| Ступени толщины (ч/з 4 см) | Диаметр, xi, см | Высота yi, м | yусл. | Отклонения | |||
| α =yi - y | α2 | Δy = =yi-yусл. | Δy2 | ||||
| 11,3 12,0 13,8 | 13,6 15,3 15,8 | 14,9 | -6,53 -4,83 -4,33 | 42,64 23,32 18,75 | -1,3 0,4 0,9 | 1,69 0,16 0,81 | |
| 14,9 14,7 14,7 15,7 14,8 16,2 17,3 16,5 | 18,1 19,5 15,3 18,1 17,6 17,5 18,6 19,5 | 18,03 | -2,03 -0,63 -4,83 -2,03 -2,53 -2,63 -1,53 -0,63 | 4,12 0,40 23,33 4,12 6,4 6,92 2,34 0,40 | 0,07 1,47 -2,73 0,07 -0,43 -0,53 0,57 1,47 | 0,05 2,16 7,45 0,0003 0,18 0,28 0,32 2,16 | |
| и т.д | … | … | … | … | … | … | … |
| ∑ α2 251,46 | ∑ Δ y2 73,15 |
yусловное- средняя высота ступени толщины.
Например: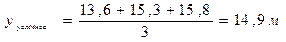 
.
Формула расчета корреляционного отношения
.
Например: 
.
Ошибка корреляционного отношения
.
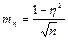Например: 
.
Значимость корреляционного отношения
.
Например: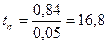 
.
Число степеней свободы:
.
Например: .
t – критерий Стьюдента на 5 % уровне значимости (определяется по таблице учебника) исходя из числа степеней свободы
t 05 = 2,045 (определяется по таблице учебника),
t r= 7,36 > t05, значит корреляция значима.
Мера линейности корреляции
.
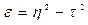Например: 
.
Основная ошибка
.
Например: 
.
По отношению меры линейности к основной ошибке судим о линейности связи.
Например: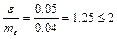 
, связь приблизительно можно считать линейной.
Степень тесноты связи между изучаемыми признаками производится по величине корреляционного отношения с помощью таблицы 6.2.
Таблица 6.2 Таблица для определения тесноты связи
| Степень тесноты связей | Величина корреляционного отношения |
| слабая | 0-0,3 |
| умеренная | 0,31-0,5 |
| значительная | 0,51-0,7 |
| высокая | 0,71-0,9 |
| очень высокая | 0,91 и выше |
Статистическое заключение
По результатам корреляционного анализа можно сделать вывод, что взаимосвязь между диаметром и высотой ствола по направлению – прямая, по тесноте – высокая, по форме – близка к линейной.
Регрессионный анализ
Постановка задачи
Математические выражения, отражающие причинно-следственные взаимосвязи и взаимодействия в системах (или модели связи) являются основными типами моделей, применяемых в области лесного дела. В качестве математической формы эмпирических моделей связи, в основном, используют регрессионные уравнения и реже – интерполяционные многочлены. В первом случае применяют различные модификации метода наименьших квадратов, позволяющие просто и достаточно надежно оценить статистическим путем разрабатываемую модель. Второй метод сводится к механической процедуре аналитического выражения числовых массивов.
Для вычисления коэффициентов регрессионных уравнений основным методом является метод наименьших квадратов, предложенный в начале XIX в. Лежандром и Гауссом. Требование метода наименьших квадратов заключается в том, что теоретические точки линии регрессии y должны быть получены таким образом, чтобы сумма квадратов отклонений от этих точек эмпирических значений была минимальной, то есть
