Уровень значимости и мощность критерия

Рассмотрим две простые гипотезы: проверяемую H ₀: θ = θ₀, и конкурирующую H ₁: θ = θ₁. С каждым S- критерием связаны ошибки двух родов. Ошибка 1-го рода — отвержение гипотезы H ₀, когда она верна; ошибка 2-го рода — принятие H ₀, когда верна конкурирующая гипотеза H ₁. Обозначим

Тогда вероятность ошибки первого рода S- критерия равна , а вероятность ошибки второго рода равна . В самом деле пусть гипотеза H ₀-верна, тогда θ = θ₀. Гипотеза H ₀— отвергается, если (x ₁, x ₂,… x _n) S. Вероятность этого равна 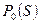. Вероятность ошибки второго рода равна 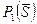, где 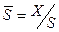, — множество значений (x ₁, x ₂,… x _n).

Опр: Вероятность ошибки первого рода α называется уровнем значимости S- критерия. Функция аргумента θ называется функцией мощности S- критерия.

Из определений следует, что Отсюда видно, что чем больше мощность в точке θ₁, тем меньше вероятность ошибки второг рода.

Параметрические критерии для распознавания двух простых гипотез H ₀ и H ₁ строят следующим образом. Сначала задается уровень значимости α, затем из множества S_α всех S- критериев с уровнем значимости α выбирается критерий S^*, для которого мощность при θ = θ₁ принимает наибольшее значение, т.е.

Такой критерий называется оптимальным или наиболее мощным.

Теорема Неймана-Пирсона.

Для любого 0≤ α ≤1 существует число С такое, что , тогда и эта вероятность минимальна среди всех критериев с уровнем значимости α.

№25 Построение оптимального критерия для проверки гипотез о параметрах нормального распределения.

Проверка гипотезы о предполагаемом законе неизве­стного распределения производится так же, как и про­верка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины— критерия согласия.

Критерием согласия называют критерий проверки ги­потезы о предполагаемом законе неизвестного распреде­ления.

Имеется несколько критериев согласия: («хи квад­рат») К. -Пирсона, Колмогорова, Смирнова и др. Огра­ничимся описанием применения критерия Пирсона к про­верке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюда­емые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Обычно эмпирические и теоретические частоты раз­личаются. Например

эмп. частоты.....6 13 38 74 106 85 30 10 4

теорет. частоты... 3 14 42 82 99 76 37 11 2

Случайно ли расхождение частот? Возможно, что рас­хождение случайно (незначимо) и объясняется либо ма­лым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу Н0. генеральная

совокупность распределена нормально, надо сначала вы­делить теоретические частоты, а затем наблюдаемое значение критерия:

(**)

по таблице критических точек распределения χ², по сданному уровню значимости а и числу степеней свободы k=s—3 найти критическую точку

Если < —^нет оснований отвергнуть нулевую гипотезу.

Если > —нулевую гипотезу отвергают.

Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае.не менее 50. Каждая группа должна содержать не менее 5—8 вариант; малочисленные группы следует объединять в одну суммируя частоты.

Замечание 2. Поскольку возможны ошибки первого и второ го рода, в особенности если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс (см. гл. XVII, § 8).

Замечание 3. Для контроля вычислений формулу (**) пре­образуют к виду