Элементы комбинаторики: схема выбора без возвращения, примеры
Выборки упорядочены.
В урне М различных пронумерованных шаров.
Условие: из урны один за другим извлекаются без возвращения в урну n шаров. В этом случае (n ≤ M).
Выборка w = (а1, а2,…, аn), где любое ai — номер шара, вынутого на i -м шаге.
Причем если одни и те же шары появляются в другом порядке, то выборки считаем различными.
n = 2 (1,2) (2,1)
Это две разные выборки.
Число таких исходов: АnM = M!/(M – n)! = N (Ω)
Выборки не упорядочены.
Если одни и те же шары появляются в другом порядке, то выборки считаются одинаковыми.
n = 3; (1,2,3) и (2,1,3) одинаковы
Число таких исходов: CnM = АnM/n!
Пример1.
На карточках написаны числа от 1 до 100. Вынем без возвращения 2 карточки. Сколько существует способов сделать так, чтобы на обеих карточках было < 10?
Решение.
Сколько существует способов выбрать из карточек с номером от 1 до 9 две карты? Схемы выбора без возвращения (выборка не упорядочена) С29 = 36.
Пример2.
Сколько существует способов поставить n человек в ряд так, чтобы м/ду А и В стояло r человек? (расстановки упорядочены)
Решение.
n = n – 2 упорядочим А и В: 2!=2 упорядочим остальные (n - 2) человек: (n - 2)! Посчитаем число, где А впереди В:
А - 1, В - r + 2, А - 2, В - r + 3 => (n - r -1) способ, А - n - r - 1, В – n
Ответ: 2(n - 2)!(n - r -1) способов.
Элементы комбинаторики: схема выбора c возвращением, примеры.
Выборки упорядочены.
Извлекаем n шаров с возвращением, т.е. извлекаем один шар, записываем его номер и кладем в урну. Так повторяем m раз подряд. w = (а1, а2,…, аm), где любое ai — номер шара, вынутого на i -м шаге. Если одни и те же шары появляются в другом порядке, то выборки считаются разными.
n = 3; (1,2,3) и (2,1,3) различны.
Число таких исходов: Mn.
Выборки не упорядочены.
То же самое, но только n = 3; (1,2,3) и (2,1,3) равные.
Число таких исходов: CnM+n -1.
Задача
По М занумерованным ячейкам распределим n дробинок. В любую ячейку может попасть любое количество дробинок от 0 до n. Будем считать, что разм. совпадает тогда и только тогда, когда в ячейке с одинаковыми номерами находится одинаковое число дробинок. Сколько существует разл. Способов размещения дробинок по ячейкам?
Решение
Обозначим хi — число дробинок в j -й ячейке. Тогда искомое число способов = числу решения ур-я х 1 + х 2 + …+ х m = n. Найдем число решений путем: * — дробинка; || — ячейки.
| * * * | * | | | | * * * * |
M = 6 ячеек.
n = 8 — дробинки
(3,1,0,0,0,4)
Схема выбора без возвращения (выборки не упорядочены)
M + n + 1 – 2 = M + n -1
Выберем n позиций для дробинок:
СnM + n – 1
(доказательство: Извлечем шар. Пусть его № = к. Это событие означает, что дробинка попала в к -ю ячейку. Число дробинок = n это объем выборки. Число ячеек — М. Число элементарных исходов = СnM + n – 1 = N (Ω), т.е. число элементарных исходов = числу сочетаний.)
Классическая вероятность: элементарный исход, события, конечная схема, определения, примеры. Вероятность и частота.
Определение вероятности
Пусть некоторый эксперимент имеет N элементарных исходов. Будем считать, что исходы не совместны, т.е. в результате конкретного эксперимента происходит только 1 элемент. исход. Элемент. исходы равновозможны. Тогда припишем каждому элементарному исходу число 1/ N. Любое подмножество множества Ω = { w 1,… wN }. Всякое элементарное событие содержится в некотором событии А назовем благоприятным событию А.
Определение
Пусть m — число элементарных исходов, благоприятных событию А. Тогда классич. вероятность события А = m / N. Обозначается как Р (А) = m / N.
Пример1
Игральная кость. Найти вероятность того, что выпадет 5 или 6.
Событие А = {5 или 6}
N = 6
Р (А) = 1/3 (2 из 6-ти возможных).
Относительная частота события А определяется равенством W (A) = m / n, где m — число испытаний, в которых событие А наступило, а n — общее число произведенных испытаний.
Вероятность и частота.
Статистический подход.
Проводим эксперимент n раз и фиксируем, произошло или нет в рез-те событие А. Пусть оно произошло k раз, тогда k/n – частота события А (для больших n близко к постоянной величине). Если отклонение k/n от этой постоянной величины с ростом n уменьшается,- устойчивость частот. Впервые это заметили, изучая демографические вопросы: % смертности в опред. возрасте для опред-х групп населения. Были попытки построить теорию, принимая за вероятность частоту события, но возникли сложности.
Геометрическая вероятность.
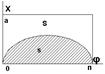
Постановка задачи: пусть G – огранич. плоская область с конечной площадью. В эт. области содержится обл. g облад-щая те-ми же св-ми. В обл. G наугад бросается точка, она может попасть в любое место обл-ти G (рис.1). Вер-ть точки попасть в g пропорциональна отношению площадей G и g и не зависит от ее формы и расположения. Т.о. вер-ть попадан. в обл. g точки, брош. в обл. G наудачу, =, по опред.: Р=S(g)/S(G), S(g) и S(G) – площ. g и G в общем виде S(g) и S(G) – меры множеств g и G.
Задача о встрече: Два лица А и В условились встретиться м/у 12 и часом дня. Пришедший первым ждёт 20 минут и уходит. Какова вероятность встречи, если приход каждого в течен. часа мож. произойти наудачу и моменты прихода А и В независимы. Решение: обозначим момент прихода А через х, а В – у. Изобразим х и у как декарт. коорд-ты, единиц. масшт. – 1 мин. (рис.2). Всевозможн. исходы можн. изобразить ввиде пар (х, у) – т. квадрата со стороной 60. Встр. состоится, если ½x – y½ ≤20 (заштрих. обл.). Область G =60 2, g = 60 2 - 2*0,5*(40*40) = 602- 402, p = (602- 402) / 602= 5 / 9.
Парадокс Жозефа Бертрана: Наудачу берём хорду в круге. Чему равна вероятность того, что её длина больше длины стороны правильного треугольника, вписанного в окружность? Решение 1: По соображен. симметрии зададим направление всем хордам, проведём диаметр, ┴ эт. направлен. Впишем в круг 2 прав-ых треуг-ка: OD = OC = R / 2 (радиус) (рис.3). Те хор-ды, кот. ∩ диаметр АВ в т-ах отр-ка CD, имеют длину > сторон прав-го ∆. Поэт. вер-ть события, кот. мы ищем: Р= CD / AB =1/2.
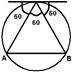
Решение 2: (рис.4) Условию задачи благоприятствуют лишь те хорды, концы которых попадают на дугу AB: Р=(дл. дуги AB)/ (дл. окр-ти) =1/3. Решение 3: Чтобы определить положение хорды, достаточно задать её середину. Бросаем т. (А) на пл-ть окр-ти, соединяя ее с центром круга и провод. хорду ч/з эт. точку, ┴ получен-му отр-ку (рис.5). Хорда длиннее стороны прав-го ∆, если т. A попадёт в круг радиусом R / 2: Р =(площ. круга R / 2) / (площ. круга R) =1/2. Причина парадокса: понятие «хорда выбир-ся наудачу в некот-ом круге» опред-ся неоднозначно. За реш. задачи принимается реш. 3-ех разн. задач.
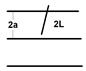
Задача Бюффона (использ-ся для эксперим-го вычислен. числа p): Пл-ть разграничена ║-ми линиями, отстоящими др. от друга на расстоян. 2 a. На пл-ть науд. брос-ся игла длиной 2 l (l < a) (рис.6). Найти вер-ть того, что игла пересечёт какую - л. прямую. Решение: Пусть x – расстоян. от центра иглы до ближайшей параллели, а j – угол м/у иглой и параллелью. Наудачу, значит: 1) Центр иглы попадает на отр-ок длинной 2 a и ┴ параллелям. 2) Угол φ попадает на отрезок [ φ 1, φ 1+Δ φ ], с вер-ью пропорц-ой Δ φ и назавис. от φ 1. 3) x и φ не зависят др. от др. Можно смоделир-ть бросан. иглы на пл-ть: игл. брос. в прямоуг-к (S) шир-ой p и выс-ой а (рис.7). Для того, чтоб. игла ∩ прямую необх. и достат., чтоб. т-ка попала в обл. х ≤ l sin φ (s). P(игла∩прям.) = (площадь s)/(площадь S) = 2 l / a π. (Пл. s = 0ò π l sin φ d φ; пл. S = a π)


Аксиоматика Колмогорова
Множество исходов некоторых экспериментов (исход эксперимента — событие элементарное) — обозначается ω
Множество всех исходных экспериментов — пространство элементарных событий — Ω
Подмножества — события
События:
1. Достоверное – событие происходит всегда при воспроизведении условий эксперимента.
2. Невозможное – событие никогда не происходит.
3. Случайные – события могут произойти или нет.
События: А=В - равносильные; А и Ā – противоположные.
События: Совместные и Несовместные (если их произведение – пустое множество АВ=Ø)
Если А=В1+В2+…+Вn, и события Вk не совместные. Т.е. ВiВj=Ø (i≠j), тогда событие А подразделяется на частные случаи В1, В2, … Вn или А можно разложить в сумму несовместных событий.
События В1, В2, … Вn образуют полную группу, если хотя бы одно из них должно произойти при каждом осуществлении комплекса условий эксперимента В1+В2+…+Вn=Ω
Система событий А называется полем событий, если
1. Ω, Ø Є А
2. А Є А, В Є А (А+В Є А, АВ Є А, А/В Є А)
Опр1. Назовём систему событий А множеств пространства Ω алгеброй множеств, если
1. Ω, Ø Є А
2. А, Ā Є А
3. А Є А, В Є А (А+В Є А, АВ Є А)
Опр2. Алгебра множеств А называется σ-алгеброй, если Аn Є А,n=1,2,… ΣАn Є А, ΠАn Є А
Опр2. Тройку символов (Ω, А,Р), где: Ω—пространство элементарных событий, А— σ-алгебра множеств, Р—вероятность А, удовлетворяющая аксиомам:
А1. для любого А Є А Р(А)≥0 (аксиома неотрицательности)
А2. Р(Ω)=1 (аксиома нормированности)
А3. АВ= Ø => Р(А+В)=Р(А)+Р(В) (аксиома аддитивности)
А4. А1 כ А2 כ…, ∩Аn = Ø => Р(∩Аn)=0 (аксиома непрерывности)
Тогда тройка этих символов называется вероятностным пространством.




