Метод моментов
Пусть x  , x
, x  … x
… x  – независимая выборка из распределения с плотностью p(x; θ
– независимая выборка из распределения с плотностью p(x; θ  ,…, θ
,…, θ 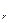 ), зависящей от параметров θ
), зависящей от параметров θ  ,…, θ
,…, θ 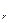 .
.
Определение: Интеграл вида
m  (θ
(θ  ,…, θ
,…, θ 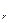 )=
)=  называется теоретическим моментом порядка k, а статистика
называется теоретическим моментом порядка k, а статистика  называется выборочным моментом порядка k.
называется выборочным моментом порядка k.
Предположим, что при k=1,2….r, все теоретические моменты m  (θ
(θ  ,…, θ
,…, θ 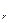 ) конечны и что система уравнений
) конечны и что система уравнений  m
m  (θ
(θ  ,…, θ
,…, θ 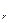 ), k=1,2,…,r однозначна разрешима, причем решение
), k=1,2,…,r однозначна разрешима, причем решение  m
m 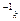 (b
(b  ,…, b
,…, b 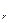 ), k=1,2,…r дается непрерывными обратными функциями m
), k=1,2,…r дается непрерывными обратными функциями m 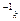 . При этих условиях имеет место
. При этих условиях имеет место
Теорема о методе моментов. Оценки  , получаемые как решения системы уравнений
, получаемые как решения системы уравнений  m
m 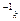 (b
(b  ,…, b
,…, b 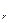 ), k=1,2,…r состоятельны.
), k=1,2,…r состоятельны.
Пример 1. Найти методом моментов по выборке x  , x
, x  … x
… x  точечную оценку неизвестного параметра λ показательного распределения с плотностью p(x)= λe
точечную оценку неизвестного параметра λ показательного распределения с плотностью p(x)= λe  (x >0).
(x >0).
Решение. Здесь неизвестный параметр один, поэтому вычисляем теоретический и выборочный моменты: m  =
= 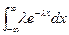 =
=  ,
, 
Искомая оценка имеет вид 
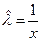 .
.
Метод наибольшего правдоподобия
Случай непрерывных распределений
Пусть x  , x
, x  … x
… x  – независимая выборка из непрерывного распределения с плотностью p(x; θ).
– независимая выборка из непрерывного распределения с плотностью p(x; θ).
Определение 1: Функция вида L(x  , x
, x  … x
… x  ; θ)=p(x
; θ)=p(x  ; θ)…p(x
; θ)…p(x  ; θ) называется функцией правдоподобия.
; θ) называется функцией правдоподобия.
Определение 2: Оценкой наибольшего правдоподобия параметра θ называют число  , которое находится из условия L(x
, которое находится из условия L(x  , x
, x  … x
… x  ;
;  )=max L(x
)=max L(x  , x
, x  … x
… x  ; θ)
; θ)
При выполнении некоторых условий, смысл которых состоит в том, что p(x; θ) – достаточно гладкая функция, а интеграл 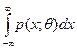 =1 достаточно быстро сходится, оценка максимального правдоподобия обладает следующими свойствами:
=1 достаточно быстро сходится, оценка максимального правдоподобия обладает следующими свойствами:
1. она состоятельна
2. она асимптотически нормальна, т.е при больших n можно рпиближенно считать, распределение  приближенно нормельным.
приближенно нормельным.
3. она асимптотически эффективна, т.е при больших n оценку  можно считать близкой к эффективной.
можно считать близкой к эффективной.
Недостатком метода является то, что иногда оценки получаются смещенными.
Случай дискретного распределения
Определение 1: Пусть P( )=P
)=P  , где
, где  – число из выборки, а
– число из выборки, а 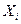 – та случайная величина, которая приняла значение
– та случайная величина, которая приняла значение  . Функция вида L(x
. Функция вида L(x  , x
, x  … x
… x  ; θ)=P(x
; θ)=P(x  ; θ)…P(x
; θ)…P(x  ; θ) называется функцией правдоподобия в дискретном случае.
; θ) называется функцией правдоподобия в дискретном случае.
Оценкой наибольшего правдоподобия параметра θ называют число 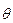 , которое находится из условия L(x
, которое находится из условия L(x  , x
, x  … x
… x  ;
; 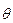 )=max L(x
)=max L(x  , x
, x  … x
… x  ; θ).
; θ).
Пример: Методом наибольшего правдоподобия найти оценку параметра λ распределения Пуассона P  =
= 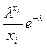 , λ>0,
, λ>0,  – целые неотрицательные числа.
– целые неотрицательные числа.
Решение. Составляем функцию правдоподобия L(x  , x
, x  … x
… x  ; λ)=
; λ)= 
И находим, что ее максимум достигается в точке  =
=  .
.
№22. Доверительные интервалы, доверительная вероятность. Построение доверительных интервалов для математического ожидания нормального распределения (с известной и неизвестной дисперсией).
Пусть x 1, x 2, …, x n — выборка из некоторого распределения с плотностью распределения p (x; θ), зависящей от параметра θ. Задача состоит в том, чтобы построить для θ доверительный интервал.
Опр: Интервал  называется доверительным, если с вероятностью (1- α) неизвестный параметр θ попадает в этот интервал. Тогда (1- α) — доверительная вероятность.
называется доверительным, если с вероятностью (1- α) неизвестный параметр θ попадает в этот интервал. Тогда (1- α) — доверительная вероятность.




