Непрерывные случайные величины

Под ФУНКЦИЕЙ РАСПРЕДЕЛЕНИЯ случайной величины Х понимают функцию F (х), определяющую вероятность того, что слу­чайная величина Х в результате испытания примет значение, мень­шее х:

F(х)=Р(Х<=х),

где х — произвольное действительное число.

Функция распределения Р(х) имеет следующие свойства:

1) F (х1)<= F(х2), если x1<=x2

2) 0<=F(х)<=1;

4)

НЕПРЕРЫВНОЙ случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют не­который промежуток и для которой существует функция f (х)=F'(х).

Функция f(х) называется ПЛОТНОСТЬЮ ВЕРОЯТНОСТИ и обладает следующими свойствами:

1) f(x)>=0;

2) ;

3) ;

4) .

Для непрерывной величины Х вероятность того, что Х примет одно определённое значение х, равна нулю:

Р(X=x)=0.

График плотности f(х) называется КРИВОЙ РАСПРЕДЕ­ЛЕНИЯ.

Математическое ожидание непрерывной случайной величины Х вычисляется по формуле

где f (х) — плотность вероятности.

Дисперсия непрерывной случайной величины Х выражается формулами

ИЛИ

Распределение вероятностей непрерывной случайной величи­ны Х называется НОРМАЛЬНЫМ, если плотность вероятности име­ет вид

где а — математическое ожидание, — среднее квадратическое отклонение X.

f(х) — функция чётная, т.е. f {х) = f (-х). Вероятность того, что нормально распределённая случайная величина Х примет значение из интервала , вычисляется по формуле

,

где — интеграл Лапласа.

Ф(x) – нечетная функция, т.е. Ф(-х)=-Ф(x). Имеются таблицы значений f(x), Ф(x) для различных значений x.

 

Некоторые непрерывные распределения, кривые распределений, основные числовые характеристики распределений Пирсона, Стьюдента и Фишера (без вывода формул" для плотностей этих распределений).

Распределение.

Определение. Пусть 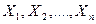- независимые случайные величины, нормально распределенные с параметрами (0,1). Другими словами,

Тогда случайная величина

имеет распределение с n степенями свободы.

Плотность каждой случайной величины имеет вид .

Распределение Стьюдента.

Пусть 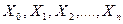- независимые случайные величины, нормально распределенные с параметрами (0,1). В статистике часто возникает случайная величина

с распределением Стьюдента с n степенями свободы. Ее плотность распределения имеет вид

, .

Распределение Фишера.

Пусть - независимые нормально распределенные случайные величины с параметрами (0,1).

Определение. Случайная величина вида

имеет распределение Фишера с параметрами p и q.

Плотность распределения:

, x 0.

График плотности f(х) называется КРИВОЙ РАСПРЕДЕ­ЛЕНИЯ.

 

№16. Неравенство Чебышева(с док-вом) Пусть случайная величина Х имеет конечные МХ и DХ. Тогда для любого ε>0 справедливо неравенство

P{│X-MX│> ε} Доказательство Неравенство Чебышева справедливо как для дискретных, так и для непрерывных случайных величин, причем доказательства для обоих случаев по существу совпадают. Мы ограничимся случаем, когда случайная величина дискретна. По определению имеем

DX= . Так как в сумме все слагаемые неотрицательны, она может лишь уменьшится, если мы отбросим часть слагаемых,поэтому

DX .Теперь суммируются лишь такие слагаемые, у которых

│ │>ε,следовательно, при замене () на сумма может лишь уменьшится,значит

DX что и т.д.

Закон больших чисел(с док-вом) Пусть S -число успехов в серии из n независимых испытаний в схеме Бернулли с вероятностью успеха p, 0<p<1. Тогда при любом t>0 справедливо равенство Доказательство Как отмечалось ранее, MS =np, DS =npq. Имеем . Применим неравенство Чебышева, положив в нем Х=S и что и т.д.

Закон больших чисел утверждает,что при больших n и при сколь угодно малых ε разность между частотой успеха S /n и вероятностью успеха в каждом испытании p по модулю меньше ε с вероятностью, близкой к 1.

Пример В большом городе в год рождается 20000 детей. Считая вероятность рождения мальчика p=0,5 найти такое число t, чтобы с вероятностью 0,99 можно было утверждать,что число рожденных мальчиков превышает число девочек не более чем на t.

Решение. Решаем задачу по схеме Бернулли с n=20000,p=0,5.Пусть S -число рождений мальчиков, тогда (n- S )-число рождений девочек;разность между ними равна(2 S -n).Найдем такое t, чтобы P{|2 S -n |>t} . Воспользуемся неравенством Чебышева: . Выбираем t из условия

 

№17. 1) Теорема Пуассона (с док-вом) Пусть Sn-число успехов в серии n независимых испытаний Бернулли. Если n→∞ и p→0 так, что np→λ, то для любого фиксированного m=0,1,2…

P{Sn=m}→

Доказательство Справедливы тождества P{Sn=m}= (1-p) = (1-1/n)(1-2/n)…(1- )(1-p) Теперь перейдем к пределу при n→∞ с учетом равенств

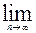
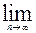= , (1-1/n)(1-2/n)…(1- )=1, (1-p) =e что и т.д.

2) Теоремы Муавра-Лапласа(без док-ва)

Локальная теорема Муавра-Лапласа Если в схеме Бернулли npq→∞, то для любого С>0 равномерно по всем │х│<=C вида x= , где m-целые неотрицательные числа, P{ }= (1+o(1)).

Интегральная теорема Муавра-Лапласа Пусть в схеме Бернулли npq . Тогда для любых -∞<A<B<∞ справедливо равенство

P{A }

Центральная предельная теорема. Если случайные величины Х1,Х2,…Хт независимы, одинаково распределены и имеют конечные математические ожидания МХ =α и дисперсии DX ,то P{ } =Ф(х).

Ошибки измерения При измерении некоторой величины α мы получаем приближенное значение Х. Сделанная ошибка δ=Х-α может быть представлена в виде суммы двух ошибок δ=(Х-МХ)+(МХ- α). Хорошие методы измерения не должны иметь систематической ошибки: МХ= α. Случайная ошибка имеет нулевое математическое ожидание Мδ=0. Пусть Dδ=σ .Для уменьшения ошибки проводится n независимых испытаний, и за оценку α берут среднее арифметическое этих измерений

= . Вычислим, какая при этом допускается погрешность. По центральной предельной теореме

P{| - α | }=P{| | } при n→∞.

№18. Простейший поток событий Рассмотрим событие, наступившее в случайный момент времени(поток событий). Пример: поступление вызовов на АТС,прибытие самолетов в аэропорт и т.д.. Основные св-ва:1) стационарность -вер-ть появления К события на любом промежутке времени t зависит только от К и t и не зависит от начала потока,при этом различные промежутки временине пересекаются. Вывод:если поток событий обладает св-вом стационарности,то вер-сть появления К события за t зависит только от К и t.

2) св-во отсутствия последействия:вер-ть появления К событий на любом промежутке времени зависит от того, что появилось или нет событие в в предш. момент времени,т.е. предыстория потока не сказ. На вероятности появления события в ближайшем будущем. Вывод:если поток обладает св-вом 2), то имеет место взаимная нез-ть появл. того или иного числа событий в предш. момент времени.

3) св-во ординарности:появление двух и более событий за малый промежуток времени практически невозможно, т.е. вероятность появления более одного события пренебрежительно мала по сравнению с вероятностью появления только одного события. Вывод: если поток обладает св-вом 3),то за беск. Малый промежуток времени может появится не более 1 события. ОПРЕДЕЛЕНИЕ: Простейшим (пуассоновским) потоком событий называют поток событий,обладающий св-вами 1-3. ОПРЕДЕЛЕНИЕ: Интенсивность потока: λ наз. среднее число событий, которое появляется в единицу времени. Если постоянная интенсивность известна, то вер-ть появления К событий простейшего потока за время t определяется формулой Пуассона:

Случайный процесс Набор случ. величин Х(t) опред. на (Ω,А) называют случайной функцией. Если параметр t играет роль времени, т.е. t принадлежит R , то такую случайную функцию называют случайным процессом. Если же t принадлежит {0,+-1,+-2…}, то случайную функцию называют случайной последовательностью.

Цепи Маркова — последовательность испытаний, в любом из которых появление только одного из К несовмесн. событий А1,А2,…Ак,причем усл. вер-ть pij(S)того,что в S-ом испытании наступит событие Аj(j=1-k) при условии,что в (S-1)-м испытании было Aj(i=1-k) не зав. от рез-тов предшеств. испытания.

ЦМ являются обобщающим понятием независимых испытаний.