Пусть x 1, x 2, …, x n — выборка из N (a, σ), причем a и σ неизвестны.
Построитьдоверительный интервал для a при заданной доверительной вероятности (1- a).
, 
Для решения воспользуемся теоремой: Пусть x 1, x 2, …, x n — выборка из N (a, σ), Статистика 
имеет распределение Стьюдента с (n - 1) степенью свободы. (Без доказательства)
Построим, пользуясь этой теоремой, доверительный интервал для a. Для этого прежде всего заметим, что плотность вероятности распределения Стьюдента с (n - 1) степенью свободы является четной и положительной функцией x. Поэтому, если 
— квантиль распределения Стьюдента с (n - 1) степенью свободы порядка 
(то есть корень уравнения F (U) = 
, где F (U) — функция распределения Стьюдента с (n - 1) степенью свободы), то 
, следовательно,
,
.
Итак,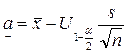 
, 
, и задача решена.
№23.Доверительные интервалы для дисперсии нормального распределения случайной величины (с известным и неизвестным математическим ожиданием).
Доверительный интервал для σ при известном параметре a.
Пусть x 1, x 2, …, x n — выборка из N (a, σ), причем σ неизвестно, а a известно.
Построитьдоверительный интервал для σ при заданной доверительной вероятности (1- a).
Воспользуемся тем, что статистика 
имеет распределение χ2 с n степенями свободы. Пусть Kn (x) — соответствующая функция распределения, 
, — квантили этого распределения порядков 
и соответственно. Тогда
,
поэтому 
, 
, и задача решена.
Доверительный интервал для σ при неизвестном параметре a.
Пусть x 1, x 2, …, x n — выборка из N (a, σ), причем σ и a неизвестны.
Построитьдоверительный интервал для σ при заданной доверительной вероятности (1- a).
Эту задачу будем решать так же, как предыдущую, только неизвестный параметр a заменим его оценкой 
. Тогда статистика 
тоже будет иметь распределение χ2, но не с n, a с (n- 1) степенью свободы. Пользуясь этим и рассуждая как в предыдущем пункте, получаем 
, 
, где , — квантили распределения χ2 с (n -1) степенью свободы порядков и () соответственно.
Статистические гипотезы, постановка задачи построения критерия проверки статистической гипотезы. Уровень значимости и мощность критерия. Параметрический критерий. Теорема Неймана-Пирсона.
Пусть случайная величина X имеет плотность p (x, θ), зависящую от параметра θ, одномерного или многомерного, принимающего значения из некоторого множества Θ. В частности, если p (x, θ) — одномерная плотность распределения и независимая выборка x 1, x 2,… x n(1) получена из распределения с этой плотностью, то n -мерная плотность, соответствует выборке (1) равна произведению
(С очевидными изменениями все это переносится и на дискретный случай, когда p (x, θ)= P { X=x }).
Значение параметра θ вполне определяет плотность p (x, θ). Те или иные гипотезы о виде неизвестного распределения или о параметрах известного распределения называются статистическими гипотезами. Статистическая гипотеза типа θ = θ 0, где θ 0 — некоторое фиксированное значение, называется простой; гипотеза типа θ 
Θ называется сложной (содержат конечное или бесконечное число простых гипотез). Проверку гипотезы проводят статистическим методом, поэтому проверку называют статистической. Гипотезу проверяют на основании выборки из ГС — это и есть статистический метод. Из-за случайности выборки в результате статистической проверки могут возникнуть ошибки и приниматься неправильные решения. Решение принимается по значению некоторой функции от выборки, называемой статистикой (это спец. статистика, которая называется статистическим критерием, который служит для отбора и проверки).
Опр: Статистический критерий К — это случайная величина, т.е. функция на множестве случайного аргумента, которая служит для проверки нулевой гипотезы.
Множество значений критерия К можно разделить на два непересекающихсяподмножества:
1) подмножество значений К, при которых H 0 принимается, называемое областью принятия гипотезы (допустимой областью).
2) подмножество значений критерия К, при которых основная гипотеза H 0 отклоняется и принимается альтернативная гипотеза H 1 , называемое критической областью.
К — одномерная случайная величина, т.е. его возможные значения некоторому интервалу. Обычно интервал — вся прямая или положительная полуось, поэтому критическая область критерия и допустимая область критерия также являются интервалами на числовой оси и, следовательно, существуют точки, которые их разделяют. Они называются критическими точками или границами критерия К.
Постановка задачи.
Относительно параметра θ имеется некоторая основная или, или проверяемая гипотеза H 0 : θ Θ. Мы должны построить такой статистический критерий, который позволяет заключить, согласуется ли выборка x 1, x 2,… x n с гипотезой H 0, или нет.
Обычно критерий строится с помощью критического множества. Из n – мерного множества всех возможных значений (x 1, x 2,… x n) выделяется такое подмножество S, называемое критическим, что при (x 1, x 2,… x n) S гипотеза отвергается, а в пртивоположном случае — принимается. Полученный с помощью критического множества S статистический критерий иногда называют S- критерием.
Мы будем рассматривать главным образом две основные гипотезы:
H 0: p (x)= p (x, θ0) — основная гипотеза;
H 1: p (x)= p (x, θ 1) — альтернативная гипотеза.
Есть задачи, в которых H 0 и H 1 — равноправны. Однако очень часто в реальных задачах эти гипотезы выступают наравнопрвно.
