Опр. Ковариацией двух сл. вел-н. Х и Y, заданных на одном и томже вероятн-ом простр-ве, наз-ся мат. ожидание произведения отклонений сл-ых вел-н Х и Y от их мат. ожиданий. Сov(X, Y)= M [(X – MX)(Y – MY)]. Она показ-ет зависят ли вел-ны Х и Y друг от др. или нет.
Теор. Если Х и Y независ-ые сл. вел-ны, то Сov(X, Y)=0. Док: По опред. Сov(X, Y)= M [(X – MX)(Y – MY)]. Раскроем скобки, тогда Сov(X, Y)= M [(X · Y – X· (MY =const)– Y ·(MX =const)+(MX·MY =const))= M (XY)– MY·MX–MX·MY+MX·MY = MX·MY–MY·MX =0, т.к. MC = C и если Х и Y независимы, то M (XY)= MX·MY и M (XY)– MX·MY =0 ■
Теор. Если сл. вел-ны Х 1 и Х 2 попарно независимы, то D(Х 1+ Х 2)=D(Х 1)+D(Х 2) и D(Х 1– Х 2)=D(Х 1)+D(Х 2). Док: D(Х 1+ Х 2)= M [(Х 1+ Х 2– M (Х 1+ Х 2))2] = M [ ((Х 1– MХ 1)+(Х 2– MХ 2))2]= M [ (Х 1– MХ 1)2+2(Х 1– MХ 1) · (Х 2– MХ 2)+(Х 2– MХ 2)2]= M [ (Х 1– MХ 1)2]+2M[(Х 1– MХ 1) · (Х 2– MХ 2)]+M[(Х 2– MХ 2)2]= D X 1+ (2 Сov(X 1, X 2)=0)+ D X 2= D X 1+ D X 2■ В ходе док-ва получили следующ. св-во D(Х 1± Х 2)= D(Х 1)+ D(Х 2) ± 2 Сov(X 1, X 2) для всех сл. вел-н Х 1 и Х 2.
Опр. Пусть на одном и томже вероят-ом простр-ве заданы сл. вел-ны X и Y. Коэффиц-ом корреляц. X и Y наз-ся число – отношение ковариации к произведен. среднеквадрат-ых отклонений этих вел-н r(X, Y)=Cov(X, Y)/ 
Опр. Ковариацией двух непрерывн. сл. вел-н Х и Y назыв-ся мат. ожид. сл-ой вел-ны (X – MX)(Y – MY), где (X – MX) – отклонение сл. вел-ны Х от соего мат. ожид. (центрирование сл-ой вел-ны.), которое выражается в интег-рале Сov(X, Y)= 
Опр. Коэффиц-ом корреляц. двух непрерывн. сл. вел-н X и Y наз-ся число r(X, Y)= Cov(X, Y)/ 
Биноминальное распределен., вычисление мат. ожид. и дисперсии бином-ой сл. вел-ны.
Опр. Пусть вероятность Р{ Х = k } = 
, где 0£ р £1, q =1– p, k = 0, 1, 2,…, n. Тогда говор., что сл. вел-на X имеет биноминальн. распр. Бином. распр. имеет сл. вел. Sn – числ. успех. в серии из n назавис. испыт. Бернулли. 
, 
.
Вычисл. МХ: Sn = X 1+ X 2+…+ X n, M Sn =M X 1+M X 2+…+M X n. Вычислим M Xk, 1 £ k £ n: M Xk =1 p +0 q = p Þ M Sn = np.
Вычисл. DХ: Sn = X 1+ X 2+…+ X n, по услов. испытания Берн. Независимы, поэтому D Sn =D X 1+D X 2+…+D X n. Вычислим D Xk при k =1,2… n: D Xk = M(Xk)2 – (M Xk)2 = M Xk – (M Xk)2 = р – р 2 = pq. Поэтому D Sn = npq.
Пуассоновское распределение
Определение Пусть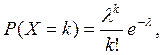 
где 
>0, к =0,1,2…
Тогда говорят, что случайная величина Х имеет пуассоновское распределение с параметром .
Вычислим математическое ожидание и дисперсию такой случайной величины. По определению имеем
Если в сумме k= 0, то соответствущее слагаемое равно нулю, так как 0! = 1. Поэтому
, (с учетом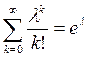 
).
^=о
Вычислим DX. Предварительно вычислим 
. Пользуясь тождеством 
имеем
Вторая сумма уже вычислена и равна , а первая равна
Поэтому 
Геометрическое распределение Определение. Пусть
, где 0 < р < 1, q= р - 1,k = 0, 1, 2,...
Тогда говорят, что случайная величина Х имеет геометрическое распределение.
Вычислим математическое ожидание и дисперсию такой случайной величины. Пользуясь теоремой о почленном дифференцировании степенных рядов, имеем
Вычислим МХ2. Пользуясь тождеством , имеем
Вторая сумма уже вычислена и равна 
, а первая равна
Поэтому 
.
